1. 引言
云计算作为一种新兴的资源共享模式,充分利用了分布式计算 [1] 和虚拟资源管理等一些技术,并且整合了网络中大量的资源,为用户提供了存储、计算、软件以及平台等服务 [2] 也给用户带来极大的便利条件,但云计算的不断发展和普及,随之而来的则是安全 [3] 方面的问题。
云计算依照部署模型可分为:公有云、私有云、社区云和混合云四种类型 [4] 。混合云一般由多个云组成,每个云都有自己的用户身份管理系统。每个云中,有云内用户信任的认证服务器,提供用户注册等请求。而云间的资源共享要求,用户在访问自己所属云之外的其它云时,要考虑与不同云用户的身份认证 [5] 和密钥协商 [6] 。
针对云计算中存在的跨域认证 [7] 问题,Xu C等 [8] 基于零知识证明和密钥托管的思想提出了一个认证方案,该方法实现了匿名性和用户真实信息的追踪。Castiglione A等 [9] 基于盲签名实现了一个跨域认证方案来支持用户身份验证,保护用户身份信息。这个方案满足了匿名性,可以避免中间人攻击,服务器的欺骗攻击等。解福 [10] 实现了基于验证元客户端到客户端的跨域认证协议,能够抵御主动和被动攻击,但该协议的交互复杂。现有的方案需要在认证服务器上保存用户的身份信息或者用来验证身份的信息,因此存在证书管理问题。2003年,Al-Riyami和Paterson [11] 提出无证书的公钥密码体制,这一体制解决了密钥托管问题。
本文提出了一个基于无证书的跨域认证方案,并且在eCK模型 [12] 下证明了所提出协议的安全性。在本文的协议中,私钥由两部分组成,不存在密钥托管问题。经过一次交互就完成了用户认证和密钥协商,提高了协议的效率,用户认证部分也充分利用了云服务器的计算能力,适合于云计算环境。
2. 预备知识
2.1. 椭圆曲线上的双线性映射
双线性对 [13] 是两个循环群间的线性映射关系。设
和
分别是阶为q的加法循环群和乘法循环群,q是大素数,且在
和
中离散对数问题都是难解的。e是
的双线性映射,要满足以下性质:
1) 双线性:对于任意
,满足
;对于任意
,有
。
2) 非退化性:若P是
的生成元,则
是
的生成元,即
。
3) 可计算性:有多项式时间算法可计算映射e。
2.2. 相关困难问题及假设
CDH(Computational Diffie-Hellman)问题:G为q阶的循环加法群,P为G的生成元,给定
(其中
),计算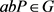 。
。
定义1:在安全参数λ 下多项式时间算法A解决CDH问题的优势为
定义2:CDH假设:对于任意多项式时间算法A ,
是可忽略的。
2.3. 安全模型
针对无证书认证密钥交换协议,有两种类型的敌手 [14] 。敌手
不知道系统主密钥,但是 可以把任意协议参与者的公钥替换成自己所选的值。敌手
知道系统所拥有的主密钥,但是不可以替换协议参与者的公钥。
可以把任意协议参与者的公钥替换成自己所选的值。敌手
知道系统所拥有的主密钥,但是不可以替换协议参与者的公钥。
表示参与者i和j的第s个会话。
Lippold [15] 等将传统的eCK模型扩展成为无证书下的eCK模型,该模型是通过挑战者C和敌手
之间进行的游戏来定义的。该游戏分成两个阶段:
阶段1:敌手可以以任何顺序进行以下查询。
Create(i):C为身份是
的协议参与者i生成公钥和私钥对。
RevealMasterKey:C 把系统主密钥返回给敌手A。
RevealSessionKey(
):如果该会话已计算出会话密钥,则把该会话密钥返回,否则返回
。
RevealPartialPrivateKey(i):C把参与者i的部分私钥返回给敌手A。
RevealSecretValue(i):C把参与者i的秘密值返回给敌手A。
ReplacePublicKey(i,pk):C把参与者i的公钥更换为A所选的值pk。
RevealEphemeralKey(
):C把参与者i的临时密钥返回给A。
Send(
,m):A向会话发送消息m,然后依据协议的执行得到相应的响应信息。
如果A认为第一个阶段的查询结束了,则A选一个新鲜会话,然后进行游戏的第二阶段,执行Test()查询。
阶段2:Test():第一阶段询问结束,A选一个新鲜会话
执行Test查询。随机选
,如果
,则返给A会话密钥,如果
,则在会话密钥空间里选一个随机的值返回给A。
在游戏的最后,A输出对b的猜测
,如果
,则A赢得游戏。A赢得该游戏的优势为 ,其中k为安全参数。
,其中k为安全参数。
定义3:新鲜会话。为参与者i和j已经结束的会话。如果下面的条件都不成立,则称是新鲜的。
1) A查询了的会话密钥。
2) A查询了i拥有的部分私钥或秘密值和会话的临时密钥。
定义4:安全性。当认证密钥交换协议达到如下条件 [16] 时,则称该协议是安全的。
1) 若攻击者诚实的转发消息,且参与者接受该会话,则参与者能获得在会话密钥空间内均匀分布的密钥。
2) 对于任意的多项式时间敌手A,能够赢得游戏的概率是可忽略的。
3. 基于无证书的跨域认证方案
基于苏航等 [17] 的无证书方案设计和CDH假设,提出了本文的协议。
3.1. 方案设计
1) 系统初始化算法
选取满足安全常数λ的阶为q的椭圆曲线循环群
和
,即
,
的生成元为P。
和
分别是加法循环群和乘法循环群,e是
的双线性映射。选取安全散列函数
,
,其中K是会话密钥空间。
域A和域B分别选取
,
作为系统主私钥即
,
,计算公钥
,
。域A和域B在各自域内公开系统参数
和
。
2) 用户部分私钥生成算法
域A内用户user向域A发出注册请求并发送自己的身份信息
,域A随机选
,计算
并把它作为用户的部分私钥,并把
发送给user。
user验证
,相等则接收k。若等式不成立,则拒绝此部分私钥。
3) 用户公私钥生成算法
用户user随机选
,计算私钥
,输出公钥
。
4) 密钥协商算法
用户user选择临时密钥
,计算临时信息
,
。选随机数
,同时用域B的公钥加密
和随机数
,得到
,把
发送给域B。
域B解密
得到
和
验证等式
,验证通过则选择临时密钥
, 计算临时信息
,计算出会话密钥
后用该会话密钥加密
得到
,把
发送给用户user。
用户user解密
得到
,确认 和
是不是相等,若相等,则可确定域B的身份,进而双方可用计算得到的会话密钥进行安全的通信。
和
是不是相等,若相等,则可确定域B的身份,进而双方可用计算得到的会话密钥进行安全的通信。
用户user计算:
会话密钥
域B计算:
会话密钥
3.2. 正确性分析
1) 域B验证用户的正确性
2) 协议的正确性
协议正确,则需证明用户user和域B计算得到了相同的会话密钥,即证明
。
用户user的计算如下:
域B的计算如下:
由计算结果可知,用户user和域B能得到一样的会话密钥。
3.3. 安全性证明
下面给出本文提出的协议在eCK模型下的安全性的证明,
和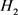 是随机预言机。
是随机预言机。
引理1:由于CDH问题是困难问题,则本文协议在
的攻击下是安全的。
证明:假设
能 以不可忽略的优势 赢得2.3节中定义的游戏。那么挑战者C可以利用
的能力解决CDH问题。C随机选
,设置
为协商用户所在域(域A)的公钥,并令
。令域A内全局系统参数为
,并把该参数发给
。
赢得2.3节中定义的游戏。那么挑战者C可以利用
的能力解决CDH问题。C随机选
,设置
为协商用户所在域(域A)的公钥,并令
。令域A内全局系统参数为
,并把该参数发给
。
令
为参与方可拥有的最多会话数,
为最多激活的用户数,
为最多进行的哈希询问次数。令
为C 解决CDH问题的优势。为了解决CDH问题,给定CDH挑战
,
和一个预言机DDH(*,*,*),C 的任务是计算
。C 模拟2.3节中定义的游戏,在游戏中C要回答
的所有询问。
在游戏开始前,C 随机选
,代表参与跨域认证的用户。随机选
,选择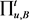 作为Test会话。
作为Test会话。
将敌手攻击的情况 [18] 分为以下几种来讨论:
1) 不知道用户的部分私钥和域B的临时密钥。
Create(i):C维护一个初始为空的列表
,其中存储的元组格式为
,如果
,C随机选
,计算
,
,设置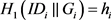 ,并在
中存储
,在
中存储
。如果
,随机选
,计算
,
, 设置
,并在
中存储
,在
中存储
,并在
中存储
,在
中存储
。如果
,随机选
,计算
,
, 设置
,并在
中存储
,在
中存储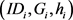 。
。
询问:C维护一个初始为空的列表
,其中存储的元组格式为
。如果
在
中,则返回
给
。否则随机选择
返回给
,并在
中存储
。
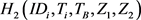 询问:C维护一个初始为空的列表
,记录的元组格式为
。如果查询的元组在
中,则返回
给
。否则按如下操作:
询问:C维护一个初始为空的列表
,记录的元组格式为
。如果查询的元组在
中,则返回
给
。否则按如下操作:
如果
,C 在列表
中找形如
的元祖,若找到,则计算
C 检查分别输入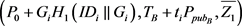 ,
,DDH预言机是否输出1。如果
和
计算正确,在
中存储
,
为
中的值。如果计算错误,则随机选
,在
中存储
,并返回
,
,DDH预言机是否输出1。如果
和
计算正确,在
中存储
,
为
中的值。如果计算错误,则随机选
,在
中存储
,并返回 给
。
给
。
如果
,在列表
中找形如
的元祖,若找到,则在
中存储
,
为
中的值。否则随机选 ,在
中存储
,并返回
给
。
,在
中存储
,并返回
给
。
RevealMasterKey:C 停止模拟。
RevealSessionKey(
):如果
,则C 停止模拟,否则把会话密钥
返回给
。
RevealPartialPrivateKey(i):如果
,则C停止模拟,否则把部分私钥
返回给
。
RevealSecretValue(i):C查找
列表,若找到形如
的元组,则返回
给
。否则执行Create(i),返回
给
。
ReplacePublicKey(i,pk):C查找
列表,若找到形如
的元组,则替换
和
为
和
,其中
,
。若没有找到,则执行Create(i),再替换
和
为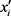 和
。
和
。
RevealEphemeralKey(i):如果
,则C停止模拟,否则C发送临时密钥给 。
。
Send(
,m):C维护一个初始为空的列表
,其中存储的元组格式为
。
如果
,则返回
给
。
如果
,C 随机选择
,并计算
C 检查分别输入 ,
,DDH预言机是否输出1,如果
和
计算正确,则在
中记录
,
为
中的值。否则,随机选
,
,DDH预言机是否输出1,如果
和
计算正确,则在
中记录
,
为
中的值。否则,随机选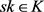 ,在
中存储
。
,在
中存储
。
如果
,则按协议规则进行回答。
Test():如果
,则C停止模拟,否则,C随机选
,并把
返回给
。
假设
能够 赢该游戏,那么
一定计算出了准确的
和
。C 有
的概率在
中找到正确的元组。 C 计算:
则 C 解决CDH问题的优势
,C以不可忽略的优势解决了CDH问题,这与CDH假设冲突。
2) 不知道用户的临时密钥和域B的临时密钥。
Create(i):C 维护一个初始为空的列表
,其中存储的元组格式为
,C 随机选
,计算
, ,设置
,并在
中存储
,在
中存储
。
,设置
,并在
中存储
,在
中存储
。
询问:C 维护一个初始为空的列表
,其中存储的元组格式为
。如果查询的元组在
中,则返回
给
。否则按如下操作:
C 在列表
中找形如
的元祖,若找到,则计算
C 检查分别输入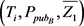 ,
,DDH预言机是否输出1。如果
和
计算正确,在
中存储
,
为
中的值。如果计算错误,则随机选
,在
中存储
,并返回
,
,DDH预言机是否输出1。如果
和
计算正确,在
中存储
,
为
中的值。如果计算错误,则随机选
,在
中存储
,并返回 给
。
给
。
若没有找到,则随机选
,在
中存储
,并返回
给
。
RevealPartialPrivateKey(i):C 查找列表
,把相应的部分私钥
返回给
。
RevealEphemeralKey(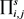 ):如果
,或者
,则C 停止模拟,否则C 发送临时密钥给
。
):如果
,或者
,则C 停止模拟,否则C 发送临时密钥给
。
Send(
,m):C维护一个初始为空的列表
,其中存储的元组格式为
。
如果
,C返回
给
,如果
,则返回
给
。否则按协议规则进行回答。
除以上询问外,其它情况和1)中相同。
假设
能够 赢该游戏,则
一定计算出了准确的
和
。C有
的概率在
中找到正确的元组。
。
则 C 解决CDH问题的优势
,C以不可忽略的优势解决了CDH问题,这与CDH假设冲突。
引理2:由于CDH问题是困难问题,则本文协议在
的攻击下是安全的。
证明:假设
能 以不可忽略的优势
赢得2.3节中定义的游戏。那么挑战者C可以利用
的能力解决CDH问题。
C随机选
,设置
作为用户所在域(域A)的系统公钥,并发送s给
。其它参数的设置和引理1的证明相同。
将敌手攻击的情况分为以下几种来讨论:
不知道用户的私有秘密值和域B的临时密钥。
Create(i):C 维护一个初始为空的列表
,其中存储的元组格式为 ,如果
,C 随机选
,计算
,
,
,设置
,并在
中存储
,在
中存储
。如果
,随机选
,计算
,
,
,设置
,并在
中存储
,在
中存储
。
,如果
,C 随机选
,计算
,
,
,设置
,并在
中存储
,在
中存储
。如果
,随机选
,计算
,
,
,设置
,并在
中存储
,在
中存储
。
询问:C 维护一个初始为空的列表
,其中存储的元组格式为
。如果查询的元组在
中,则返回
给
。否则按如下操作:
如果
,C 在列表
中找形如
的元祖,若找到,则计算
C检查分别输入
,
,DDH预言机是否输出1。如果
和
计算正确,在
中存储
,
为
中的值。如果计算错误,则随机选
,在
中存储
,并返回
给
。
如果
,在列表
中找形如
的元祖,若找到,则在
中存储
,
为
中的值。否则随机选
,在
中存储
,并返回
给
。
RevealMasterKey:C把主私钥返回给
。
RevealPartialPrivateKey(i):C把部分私钥
返回给
。
RevealSecretValue(i):如果
,则停止模拟,否则C查找
列表,若找到形如
的元组,则返回
给
。否则执行Create(i),返回
给
。
Send(
,m):C维护一个初始为空的列表
,记录的元组格式为
。
如果
,则返回
给
。
如果
,C随机选择
,并计算
C检查分别输入
,
,DDH预言机是否输出1。如果
和
计算正确,则在
中记录
,
为
中的值。否则,随机选
,在
中存储
。
如果
,则按协议规则进行回答。
除以上询问外,其它情况和引理1的证明1)中相同。
假设
能够 赢得该游戏,则
一定计算出了准确的
和
。C有
的概率在
中找到正确的元组。C计算:
则C解决CDH问题的优势
,C以不可忽略的优势解决了CDH问题,这与CDH假设冲突。
剩余情况和引理1类似。
由以上引理的证明,可知本文所提出的协议在eCK模型下是安全的。
4. 性能分析与比较
本文协议和文献 [8] [10] 的协议在构造上有差别,所以从方案的交互次数、加解密次数方面比较了这

Table 1. Performance comparison of different solutions
表1. 各方案性能比较
三个方案。
和文献 [8] 和文献 [10] 相比,本文解决了密钥托管问题,而且交互次数和加解密次数都相应的减少。文献 [8] 基于零知识证明实现了方案的匿名性和可追踪性,但是缺乏对所提出方案详细的安全性证明。文献 [10] 所提出协议的参与方有四方,交互过于复杂,且对于方案的安全性也是给出了相应的分析缺乏详尽的证明。分析说明,本文的方案保证了安全性的同时,还降低了开销。
5. 结语
本文基于无证书提出了一个云计算下的跨域认证密钥交换协议。实现了用户的跨域认证,降低了服务器的压力,充分保证了用户的密钥安全,与同类协议相比(表1),提高了认证和密钥协商的效率。
基金项目
国家自然科学基金(10007016201201)。