1. 引言
热效应在固体激光器中是不可避免的,尤其是在大能量光束泵浦激光介质时。无辐射弛豫和量子亏损是产生热效应的主要因素 [1] ,以及浓度猝灭 [2] 和能量传递上转换等机制也有一定的热贡献 [3] 。在LD端面泵浦激光系统中,对于激光介质的热负荷更多的是关注点在于泵浦光束端面泵浦聚焦为一个很小的尺寸,而泵浦光束紧密聚焦导致了高泵浦沉积能量和高热负荷密度,最终引起激光晶体产生各种热机械和热光效应,如热透镜效应、热致双折射、热致形变等 [4] [5] [6] 。对于端面泵浦激光介质的热效应研究已经有很多报道 [7] [8] [9] ,但是大多集中于用各向同性激光介质来近似各向异性激光介质,并以圆柱形为基础的解决方案研究立方晶体的热效应问题。此种研究方法忽略了各向异性激光介质自身在各轴向上参数的不同(包括热导率、热膨胀系数和热光系数等),采用各向同参数的模型建立方法,虽然对之后的计算过程起到了很大程度上的简化,但在整个模型的建立上就出现了一定的偏差,导致了晶体在各个轴向上的热焦距等结果的偏差。因而关于激光晶体的各向异性问题仍需要深入考虑。
本文的主要内容是建立了一个关于各向异性激光介质的温度场分布模型,考虑实际中立方晶体端面和侧面的冷却机制,采用端面对流、侧面恒温的近似方式来求解热传导方程。基于MATLAB仿真软件,将其结果应用于双端泵浦Nd:YVO4激光晶体中。在对Nd:YVO4晶体热效应的研究过程中,我们对其泵浦功率、泵浦光斑、长度–浓度积对晶体热效应的影响进行了详细分析,这将对Nd:YVO4激光器的晶体参数选取、热补偿及腔型设计提供理论支持。
2. 各向异性激光介质热模型
在LD端面抽运全固态激光器中,通常采用冷却循环水来控制激光晶体周围温度。当泵浦光聚焦进入激光晶体端面中心时,晶体侧面采用封闭冷却循环水来进行温度控制,而晶体的两个端面与周围环境主要是对流冷却。
如图1所示,为三维各向异性立方晶体,由此得出激光介质在直角坐标系下的一般稳态热传导方程,如下所示:
(1)
这里,
是晶体温度分布,
、
、
分别是沿x、y、z三个不同轴向上的热传导系数,
是热源密度函数。
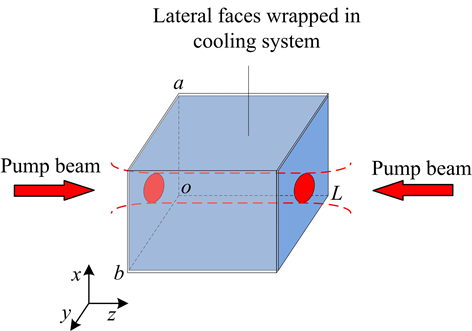
Figure 1. The thermal model of an anisotropic slab crystal
图1. 各向异性立方晶体热模型示意图
由于研究过程中采取双端泵浦立方激光晶体,并且考虑到泵浦光束在晶体内部呈高斯线型,由此根据图1得出晶体热源函数项为:
(2)
其中
为中心热源,表示为:
(3)
这里,
为泵浦光束腰,
为晶体对泵浦光吸收系数,
为吸收的泵浦功率,
是量子亏损,
其是由荧光量子效应和内损耗决定的,其中
为量子效率,
、
分别是泵浦光和输出激光波长。
考虑到端面泵浦固体激光系统实际运行条件,激光晶体放置于具有高导热性的紫铜热沉中,紫铜热沉采用高流速的水冷循环进行散热,通常情况下激光晶体侧面的温度基本可以控制在制冷温度。对于晶体通光端面,根据空气的导热系数,此处可以近似看作常规的热传导边界来处理。因此可以得到边界条件如下:
(4)
其中
为制冷系统温度,
为外界环境温度,
为晶体通光端面与外界空气的对流换热系数。
针对方程(1)和方程(4)所描述的热传导方程,利用积分变换法进行求解。首先,函数
对变量x、y进行积分变换:
逆公式:
(5)
(6)
积分变换:
(7)
(8)
其中,符号“~”表示对变量x的变换,符号“—”表示对变量y的变换。
基于以上积分变换式,简化掉方程(1)中对
及
的偏微分,依据边界条件,可得:
(9)
(10)
这里,
、
的特征值分别有方程
和
(即
和
)确定。
设激光晶体侧面相对温度为0,则晶体上某点的实际温度即为该点相对温度与
之和,用积分变换式(7)和(8)对热传导方程(1)和边界条件的x和y逐次进行积分变换:
(11)
(12)
(13)
令
,其中:
(14)
将式(3)代入上式可得:
(15)
这里,定义
、
为:
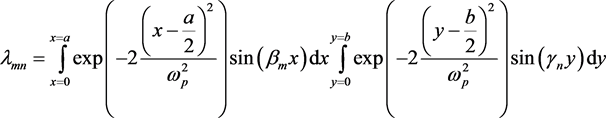 (16)
(16)
(17)
依据热传导方程(11)满足边界条件(12)和(13),由此解得:
(18)
其中:
(19)
(20)
(21)
依据式(5)和式(6),对式(18)进行积分逆变换得到:
(22)
结合上述中给出的中间参量的关系式,最终获得了各向异性晶体温度场分布的解析表达式:
(23)
对于各向异性激光介质的热透镜效应,其主要成因是在晶体内部随着温度场分布不均导致晶体折射率发生改变,并且随着出现热应力的不同导致晶体内部出现各处不同的应变分布,最终导致了傍轴相干光束出现了光程差。因抽运而在晶体内产生的光程差为:
(24)
这里,等式右边第一项是热值折射率导致的光程差,其中
为热光系数,
;第二项是热致轴向伸长形成的光程差,其中n为初始温度时晶体的折射率,
为泊松比,
为晶体热膨胀系数;第三项是热致双折射产生的光程差。各向异性晶体的热致双折射产生的光程差相对于前两项基本可以忽略。因此总光程差的表达式可以化简为:
(25)
在激光晶体内部温度分布的不均匀性导致了光线通过晶体中心与晶体边缘时光程有所不同,这类似于光线通过一个透镜的情况,所以将这个效应称之为热透镜效应。上述原因导致的光程差与热透镜焦距
之间有如下关系:
(26)
3. 仿真结果分析
针对于热效应相对较为严重的Nd:YVO4激光器,本节将基于MATLAB仿真软件,采用上述中所获得的解析式对Nd:YVO4激光晶体的热效应进行分析研究。
对于Nd:YVO4晶体,其导热系数为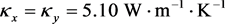 ,
。端面的换热系数为
。设定Nd:YVO4晶体尺寸为
,由于不同Nd3+离子掺杂浓度对应的晶体吸收系数是不同的,经过测量此处选取掺杂浓度为0.3at.%,对应的吸收系数为
。选取泵浦激光中心波长为
,泵浦激光束腰大小为
,输出激光中心波长
。激光系统的制冷温度为
,环境温度为
。在泵浦功率为
(双端各30W)时,给出了Nd:YVO4激光晶体温度场分布截面图,如图2所示,其中图2(a)为晶体通光轴X=0,YZ截面温度分布;图2(b)为晶体端面
,XY截面温度分布。从图中可以看出,晶体最高温度位于晶体两端面抽运中心处,晶体温升沿通光轴向两端逐渐降低,基本呈类高斯分布线型,径向由中心向晶体边缘逐步降低,基本呈由圆向方转变分布。
,
。端面的换热系数为
。设定Nd:YVO4晶体尺寸为
,由于不同Nd3+离子掺杂浓度对应的晶体吸收系数是不同的,经过测量此处选取掺杂浓度为0.3at.%,对应的吸收系数为
。选取泵浦激光中心波长为
,泵浦激光束腰大小为
,输出激光中心波长
。激光系统的制冷温度为
,环境温度为
。在泵浦功率为
(双端各30W)时,给出了Nd:YVO4激光晶体温度场分布截面图,如图2所示,其中图2(a)为晶体通光轴X=0,YZ截面温度分布;图2(b)为晶体端面
,XY截面温度分布。从图中可以看出,晶体最高温度位于晶体两端面抽运中心处,晶体温升沿通光轴向两端逐渐降低,基本呈类高斯分布线型,径向由中心向晶体边缘逐步降低,基本呈由圆向方转变分布。
在此基础上进一步对泵浦功率、泵浦光斑半径及晶体长度-浓度积对激光晶体热效应的影响进行分析。
图3为不同抽运功率条件下晶体中心轴线温度分布图,所选抽运功率为
。可以看出,随着抽运功率增加,晶体中心轴向温度梯度相应的增加,因轴向伸长所产生的热透镜效应随之增强,相应的热焦距变短。因此在注入抽运功率的过程中,要考虑到晶体所能承受的温度分布,防止晶体出现热
 (a)
(a)  (b)
(b)
Figure 2. The temperature distribution of the Nd:YVO4 anisotropic crystal. (a) X = 0, YZ plane; (b) Z = −L/2(Z = L/2), XY plane
图2. 各向异性Nd:YVO4晶体热效应温度场分布图。(a) X = 0, YZ面温度分布;(b) Z = −L/2 (Z = L/2), XY面温度分布
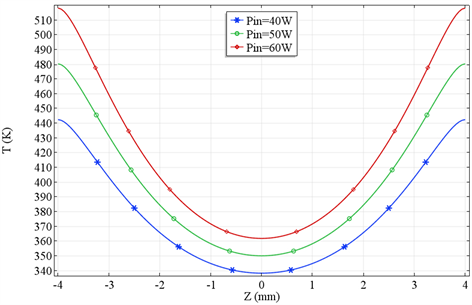
Figure 3. The temperature distribution of the Nd:YVO4 crystal center axis under the different pump power
图3. 不同泵浦功率下Nd:YVO4晶体中心轴温度分布
断裂。图4为不同抽运光斑半径条件下晶体中心轴线温度分布图,所选抽运功率为
。从图中可以得出,随着泵浦光斑半径的减小,晶体中心轴线的总体温度增高,但其相应的温度梯度差相对变化较小,即晶体轴向伸长所产生的热透镜效应也没有明显增加。由以上两方面可知,泵浦功率的增加加剧了晶体温度梯度的上升,泵浦光斑半径的减小增高了晶体的总体温度。综合以上两点,在设计实验方案时应适当的选取较大的抽运光斑半径,这样既可以实现缓解晶体的热效应,又可以因为功率密度的降低适当提高注入抽运功率。
图5为Tm晶体在不同注入抽运功率下晶体热焦距的变化曲线,设定采取相同的长度–浓度积(4at.%.mm)。图中给出了各向异性Nd:YVO4晶体平行于c轴和垂直于c轴的热焦距曲线,从中可以看出,两个方向均具有正透镜效应,且随着注入功率的增加,热透镜效应逐渐增强,热焦距变短。两个轴向的热焦距不相同是因为Nd:YVO4晶体折射率、热光系数以及热膨胀系数的各向异性所致。对于相同长度–浓度积下,其热焦距基本一致,这证明了晶体的长度–浓度积可以作为一个参量来进行考量。但是,在相同长度–浓度积时,晶体端面的温度分布却又很大差别。图6为相同长度–浓度积时在Z = L/2,X = 0沿Y轴(晶体端面径向)晶体温度分布,从图中可以看出晶体端面温差随浓度降低而降低,所以当晶体长度–浓度积为定值时,适当降低晶体掺杂浓度或者增加晶体长度,可以有效地减小晶体内的温度梯度,缓解晶体热效应。
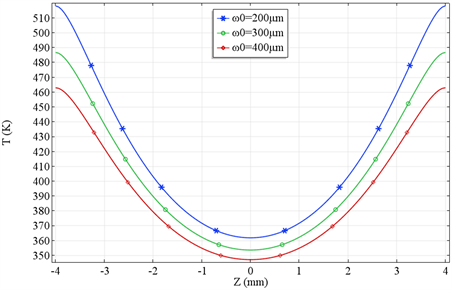
Figure 4. The temperature distribution of the Nd:YVO4 crystal center axis under the different waistradius
图4. 不同泵浦光斑半径下Nd:YVO4晶体中心轴温度分布

Figure 5. The thermal focal length perpendicular and parallel to the c axis under different pump powers (the product of crystal length and doping concentration is constant)
图5. 相同长度–浓度积下晶体热焦距随抽运功率的变化曲线
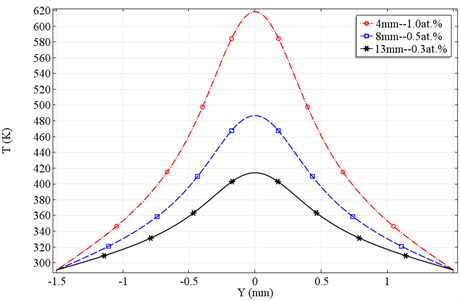
Figure 6. The temperature distribution of the Nd:YVO4 crystal at Z = −L/2 (Z = L/2) and X = 0 planes along Y axis (the product of crystal length and doping concentration is constant)
图6. 相同长度–浓度积下Nd:YVO4晶体Z = −L/2 (Z = L/2),X = 0沿Y轴的温度分布曲线
4. 结论
本文基于各向异性立方激光介质的实际工作条件建立了各向异性激光晶体的温度场分布模型。采取端面传热、侧面恒温的近似方式,给出了各向异性立方晶体温度场分布的详细求解过程。并将该模型应用到Nd:YVO4激光晶体上,研究得到如下结果:在晶体参数一定时,热透镜效应随泵浦功率密度的增加而增强;热致形变所产生的热透镜效应在Nd:YVO4晶体中起主导作用;当晶体长度-浓度积为定值时,虽然热焦距变化趋势不变,但仍需适当降低晶体掺杂浓度并增加晶体长度以达到很好地减小晶体内的温度梯度,缓解晶体热效应。该结论不仅可以为双端泵浦Nd:YVO4激光器的晶体参数选取、热补偿及腔型设计提供理论支持,同时该热分布模型也可对其他各向异性立方晶体的热分析起到一定的指导意义。
NOTES
*通讯作者。