基于混沌时间序列的潜油柱塞泵动液面预测研究

Study of Forecasting Producing Fluid Level of Submersible Reciprocating Pump on the Basis of Chaotic Time Series

摘要: 依托嵌入式计算机系统及自动控制技术，潜油柱塞泵在油田原油生产过程中得到大范围普及应用，这极大地提高了原油的开采效率。潜油柱塞泵的核心是位于井下的潜油直线电机，地面通过计算机控制井下电机的冲次、冲程等运行状态，使其与油井油藏状态相适应，从而在原油生产过程中达到高效、节能的目的。目前潜油柱塞泵的冲次控制方法是建立在动液面时间序列预测和计算的基础上的，本文介绍一种基于混沌时间序列的动液面预测计算方法，并与线性预测方法进行对比分析，最终得到能够满足潜油柱塞泵冲次优化控制的动液面预测方法。本文的研究内容为潜油柱塞泵的计算机控制提供了理论和应用依据。

Abstract: Relying on the embedded computer system and automatic control technology, the submersible plunger pump is widely used in crude oil production, which improves the efficiency of crude oil extraction greatly. The core of the submersible plunger pump is the submersible linear motor which is located underground. The operation state, such as the impulse and the stroke, of the motor is controlled by computer on the ground, which can adapt the computer to the state of the oil wells to achieve higher efficiency and save more energy in the production of crude oil. Currently, the impulse control of the submersible plunger pump is based on the prediction and calculation of the time series of dynamic liquid surface. Our paper presents a method for predicting dynamic liquid surface on the basis of chaotic time series and analyzes its advantages compared with the linear prediction method. By this way, the dynamic liquid surface prediction method can be obtained to optimally control the submersible plunger pump impulse. Our research provides the theoretical and practical basis for the computer control of the submersible plunger pump.

1. 引言

随着嵌入式计算机系统性能的大幅提升，依托自动控制理论和技术，各种新型油田抽油机高效、节能的智能化运行得以实现。这其中较为突出的高能效抽油机潜油柱塞泵，以其结构简单、容易操控等特性引发业内广泛关注，并在国内部分油田成规模应用生产 [1] 。

为进一步发挥潜油柱塞泵的优势，提高其在实际应用中的产油量，需要对其自动控制性能进行改进，其中最为重要的是对其冲次控制方法的优化。而若想得到较好的冲次优化效果，需要研究一种准确度较高的动液面预测方法，只有准确预测得到动液面高度数据或变化趋势，才能有针对性地采用冲次优化算法提高原油产量并降低开采机械的能耗。因此，本文的研究内容是潜油柱塞泵计算机控制优化的前提和基础，具有重要的理论和应用价值 [2] 。

2. 潜油柱塞泵原理及结构

潜油柱塞泵是一种以直线电机为驱动的新型抽油机，其结构如图1所示。潜油柱塞泵主要由井下和地面两部分组成，井下部分主要包括直线电机、抽油泵和潜油电缆等，地面部分主要是直线电机的控制装置和配电装置等。其最大的特点是，省略了传统抽油机的抽油杆，因此避免了油杆与油管的偏磨问题，而且不存在将旋转运动转换为直线运动的转换设备，可以有效而直接的利用直线电机产生的动能，因此大幅度提高了机采效率。

潜油柱塞泵的直线电机定子固定在油井底部，动子通过推杆直接与抽油泵的游动凡尔相连，抽油泵与油管相连，直线电机通过潜油电缆与地面控制及配电系统相连。潜油柱塞泵工作时，直线电机由地面控制柜内的嵌入式计算机通过潜油电缆控制，直线电机动子做往复运动，带动游动凡尔，不断将套管内

Figure 1. Structure diagram of submersible reciprocating pump

图1. 潜油往复抽油机结构示意图

液体吸入泵腔内，并将其通过油管举升至地面井口处。目前常用的潜油柱塞泵直线电机为永磁直线电机，外径110 mm、长6 m，额定电压660 V、最大输出电流50 A、最大输出功率30 KW、额定推力24,000 N、最大推力35,000 N、动子行程123 cm，其冲次可由地面控制系统设定。

随着潜油柱塞泵应用的增多，逐渐发现其在实际使用直线电机工作状态需要与油井汲液能力相匹配才能使采油效率最高，或者说嵌入式计算机控制潜油柱塞泵的冲次状态需要与井下动液面的高度相匹配，才能使抽油机械的效率最佳 [3] [4] 。

3. 动液面时间序列的特性分析

本文研究的潜油柱塞泵主要应用在油田开发中后期的油井或贫油井，并且有注水井配合工作。相比其他油井，这类油井的动液面是十分不稳定的，主要受到柱塞泵自身工作状态、地下油流状态及注水井状态等因素影响。有必要对潜油往复抽油机油井的动液面时间序列进行分析，以揭示其特性 [5] 。

3.1. 动液面数据的采集

本文对大庆油田采油厂的14口使用潜油往复抽油机的油井进行了跟踪测试，在一段时间内，所在作业区每日对油井动液面测量一次，采样时做多次测量取平均值处理。其中动液面使用超声波测距仪进行测量，记录为当日动液面测量值。通过对十余口潜油往复抽油机的测试分析，由于周围环境相对复杂，可能存在多口其他油井或注水井等，这些外在因素的影响加上泵自身状态的变化，动液面变化的周期性不明显。以葡54-12井为例，井深1202.6 m，图2和给出其动液面的变化数据。

3.2. 动液面数据的预处理

动液面预测需要完整、丰富和准确的时间序列样本。由于实际生产过程中，动液面原始数据经常会出现不连续，并间杂很多异常值，如果直接利用这样的原始数据进行动液面预测，会降低预测的可信性和准确度。因此，需要首先对原始数据进行预处理，对异常数据、不良数据进行剔除并补足缺损数据是

Figure 2. Producing fluid level of oil well 54-12

图2. 葡54-12井动液面变化

进行准确、合理动液面预测的前提和基础。处理这些异常数据，首先需要找到这类数据，即数据筛选，主要的处理对象是非空缺类数据，经常采用的方法是分段阈值筛选法。针对时间序列的变化特点，将其划分为若干区段，对不同区段内的动液面变化设定上限阈值和下限阈值，利用阈值对区间内数据进行筛选，然后在通过修正方法对这些异常数据进行修正和补全 [6] [7] [8] 。

根据空缺异常数据的种类，其补全的方法主要有两种。一种是缺失值的补全，另一种是待补足数据的补全。对于非空缺类异常数据，处理方法相对较多，主要有：1) 插值法、2) 纵向对比法、3) 横向对比法、4) 经验修正法、5) 概率统计法、6) 曲线置换法等。按照非空缺类异常数据的种类，其处理方式主要是：含有冲击类的数据可采用4)、5)、6)等方法；毛刺类原始数据可采用1)、4)等方法；极值类数据可以采用2)、3)、4)、5)等方法进行处理。

3.3. 动液面时间序列混沌特性的识别

3.3.1. 饱和关联维数法

关联维数法是识别混沌序列比较常用的方法。如果一个序列是随机序列，随着嵌入维数的增大，关联维数也会相应增大，不会进入饱和状态。如果一个序列的关联维数逐渐进入到饱和状态，则说明这个序列具有混沌特性。可用G-P算法计算其饱和关联维数，图3给出了葡54-12井动液面时间序列的 $\ln C\left(r\right)\text{-}\ln \left(r\right)$ ， $C\left(r\right)$ 是相关函数，r是 $Y_i$ 为球面中心的半径， $\ln C\left(r\right)\text{-}\ln \left(r\right)$ 曲线上直线段斜率就是关联维数 [9] [10] 。

3.3.2. 最大Lyapunov指数法

Lyapunov指数是一个定量描述混沌运动对初始条件敏感度的量。混沌运动具有对其初始条件极为敏感的特征，即便轨道是由非常靠近的初始值形成的，也会随着时间快速分离。

如果用 $x_{n+1}=F\left(x_n\right)$ 表示一个系统，那么 $\left|\text{d}F/\text{d}x\right|$ 的取值决定了最初的两点迭代之后是互相聚合还是互相发散。如果 $\left|\text{d}F/\text{d}x\right|>1$ ，那么经过迭代，它们互相发散。如果 $\left|\text{d}F/\text{d}x\right|<1$ ，那么经过迭代，它们互相聚合。在迭代的进程里， $\left|\text{d}F/\text{d}x\right|$ 取值不是确定的，这表明它们运动的趋势也是处于不断变化的状态之中。通过将迭代次数进行平均化处理，可以在一定的时间范畴之内观察相邻状态是聚合还是发散。所以，设 $\lambda$ 是平均迭代所引起的发散程度中的指数。容易得到，n次迭代后，原距离为 $\epsilon$ 的两点此时距离为：

Figure 3. The $\ln C\left(r\right)$ versus $\ln \left(r\right)$ plots for producing fluid level time series

图3. 动液面时间序列 $\ln C\left(r\right)\text{-}\ln \left(r\right)$ 曲线

$\epsilon {\text{e}}^{n\lambda \left(x_0\right)}=\left|F^n\left(x_0+\epsilon \right)-F^n\left(x_0\right)\right|$ (1)

取极限 $\epsilon \to 0$ ， $n\to \infty$ ，则式(1)为：

$\lambda \left(x_0\right)=\underset{n\to \infty }{\lim }\underset{\epsilon \to 0}{\lim }\frac{1}{n}\ln \left|\frac{F^n\left(x_0+\epsilon \right)-F^n\left(x_0\right)}{\epsilon }\right|=\underset{n\to \infty }{\lim }\frac{1}{n}\ln {\left|\frac{\text{d}{F}^n\left(x\right)}{\text{d}x}\right|}_{x=x_0}$ (2)

经过简化计算得到：

$\lambda =\underset{n\to \infty }{\lim }\frac{1}{n}{\displaystyle \underset{i=0}{\overset{n-1}{\sum }}\ln {\left|\frac{\text{d}{F}^n\left(x_i\right)}{\text{d}x}\right|}_{x=x_i}}$ (3)

式(3)中， $\lambda$ 为原动力系统的Lyapunov指数，其取值与选择初始值无关，表征了系统经过多次迭代后，平均每次迭代引起指数分离中的指数 [11] 。

如果 $\lambda <\text{0}$ ，则系统具有稳定的不动点；如果 $\lambda =\text{0}$ ，则对应了系统的周期解或者分岔点；如果 $\lambda >0$ ，则说明系统具有混沌特征。

本文采用小数据量方法取动液面时间序列的最大Lyapunov指数。表1分别给出了演化次数为50、100、150、200、250、300时，潜油往复抽油机油井动液面时间序列的最大Lyapunov指数，图4和图5分别给出了演化次数为100和300时 $y\left(i\right)$ 的变化趋势。观察表1、图4和图5能够看出，两油井动液面时间序列的最大Lyapunov指数均为正数，证明了两个时间序列都具有混沌性的判断。同时，可以观察到多数时间内，A油井的动液面时间序列的最大Lyapunov指数明显大于B油井的最大Lyapunov指数，并且其随演化次数的增加波动较大，B油井动液面时间序列的最大Lyapunov指数则相对稳定。

3.4. 动液面时间序列最大预测时间

一个系统演化的非确定性和随机性可以形象地称之为蝴蝶效应。最大Lyapunov指数可以表征一个系统的这种蝴蝶效应的程度。它定量地描述了一个相空间中两个相邻轨迹的发散情况。混沌系统本质上是遵循某一确定性的规律的，这也说明混沌系统存在一个最大可预测时间的。要对一个混沌系统的运行轨迹进行预测，需要确定其预测时间在这个尺度之内，才能保证预测的有效性 [12] [13] 。

在系统运行的过程中，两相邻轨道距离的初始值为 $\delta x\left(0\right)$ ，经过一段时间的演化后，它们之间的最大距离分量可以表示为：

$\delta x\left(t\right)=\delta x\left(0\right){\text{e}}^{{\lambda }_{1}t}$ (4)

t为演化时间，当 $\frac{\delta x\left(t\right)}{\delta x\left(0\right)}$ 超出某个阈值c的时候，我们就认为轨道发散。这时的系统运动是不可预测的，而演化过程中的这个时间称为临界点时间 $t_0$ 。则：

$c=\frac{\delta x\left(t\right)}{\delta x\left(0\right)}={\text{e}}^{{\lambda }_1{t}_0}$ (5)

$t_0=\frac{1}{{\lambda }_1}\ln c$ (6)

Table 1. Largest Lyapunov exponent of producing fluid level time series

表1. 动液面时间序列的最大Lyapunov指数

Figure 4. Largest Lyapunov exponent of producing fluid level time series (i = 100)

图4. 动液面时间序列的最大Lyapunov指数(i = 100)

Figure 5. Largest Lyapunov exponent of producing fluid level time series (i = 300)

图5. 动液面时间序列的最大Lyapunov指数(i = 300)

一般情况下，当轨线间距达到原来距离的几倍或者十几倍 $\left(c~10,\ln c~1\right)$ 的时候，轨迹就难以确定了。因此，混沌系统的最大可预测时间简化表示为：

$t_0~\frac{1}{{\lambda }_1}$ (7)

式(7)中的 $t_0$ 为Lyapunov时间，也就是可预测的最大时间。一般情况下，最大Lyapunov指数愈大，可预测最大时间 $t_0$ 响应的愈短，这种情况说明此系统的预测性比较差。因此，根据上一节中求得的最大Lyapunov指数，可以预估出动液面时间序列的一个可预测最大时间：

1) A井动液面时间序列的可预测最大时间 $t_0$ 为1/0.1305~1/0.2318。所以，A井的动液面序列可预测最大时间大概为4天。

2) B井动液面时间序列的可预测最大时间 $t_0$ 为1/0.0457~1/0.319。所以，B井的动液面序列可预测最大时间大概是31天。

4. 动液面时间序列的预测

4.1. ARMA动液面线性预测模型

时间序列分析中，ARMA是最常用的模型之一，它有很好的逼近平稳过程的能力。ARMA模型采用如下描述定义：如果时间序列 $\left\{X_t,t=0,\pm 1,\cdots \right\}$ 对于每个t，期望 $E\left(X_t^{\text{2}}\right)<\infty$ ，且 $E\left(X_t\right)$ 是与t无关的常数，对于每个k，协方差 $\text{Cov}\left(X_t,X_{t+k}\right)$ 与t无关，则序列 $\left\{X_t\right\}$ 称为平稳的。ARMA模型的建模方法同一般时间序列建模步骤类似，采用Box-Jenkins方法，这种建模只遵循序列自身的变化规律，采用外推的方式来表现时间序列的变化。建模的过程主要分为三个步骤：1) 时间序列平稳性检验；2) 模型的识别、参数估计及诊断检验；3) 模型的预测。

在实际的模型建立过程中，大多数序列都能用低阶模型取得较好的拟合效果，阶数p，q，P和Q的值通常取作0，1或2。为得到更好的拟合结果，可以将阶数 $\left(p,q\right)\times \left(P,Q\right)$ 的选择范围确定在一个区间 $1\le p+q\le {\lambda }_1$ ， $1\le P+Q\le {\lambda }_2$ ，在该区间中拟合尽可能多的模型，根据BIC准则(Bayesian Information Criterion)选取拟和优度统计量最优的模型。

$\text{BIC}=-2\ln \left(L\right)+\left(p+q+1\right)\ln \left(n\right)$ (8)

式中：L——一步预测时模型的高斯似然数；

n——一步预测时的残差个数。

采用极大似然估计的方法求取模型中的参数，通过似然函数：

$L\left(x_1,x_2,\cdots ,x_n,\theta \right)=f\left(x_1,\theta \right)f\left(x_2,\theta \right)\cdots f\left(x_n,\theta \right)$ (9)

选取 $\theta =\hat{\theta }$ ，使得：

$L\left(x_1,x_2,\cdots ,x_n,\hat{\theta }\right)=\underset{\theta \in \Theta }{\max }\left\{f\left(x_1,\theta \right)f\left(x_2,\theta \right)\cdots f\left(x_n,\theta \right)\right\}$ (10)

则 $\hat{\theta }=g\left(x_1,x_2,\cdots ,x_n\right)$ 就是 $\theta$ 的极大似然估计值。

根据BIC准则，由公式(8)、公式(9)和公式(10)建立油井的动液面时间序列的ARMA模型。

BIC最小值为7.6484，对应各参量， $p=6$ ， $q=4$ ， ${\varphi }_1=-\text{0}\text{.7464}$ ， ${\varphi }_2=-\text{0}\text{.3726}$ ， ${\varphi }_3=-\text{0}\text{.4819}$ ， ${\varphi }_4=-\text{1}\text{.032}$ ， ${\varphi }_5=-\text{0}\text{.2172}$ ， ${\varphi }_6=\text{0}\text{.04302}$ ， ${\theta }_1=\text{0}\text{.499}$ ， ${\theta }_2=\text{0}\text{.215}$ ， ${\theta }_3=\text{0}\text{.3904}$ ， ${\theta }_4=\text{0}\text{.9314}$ ，不计白噪声项，油井动液面ARMA模型：

$\begin{array}{c}{X}_t=-\text{0}\text{.7464}{X}_{t-1}-\text{0}\text{.3726}{X}_{t-2}-\text{0}\text{.4819}{X}_{t-3}-\text{1}\text{.032}{X}_{t-4}-\text{0}\text{.2172}{X}_{t-5}\\ +\text{0}\text{.04302}{X}_{t-6}+\text{0}\text{.499}{\epsilon }_{t-1}+\text{0}\text{.215}{\epsilon }_{t-2}+\text{0}\text{.3904}{\epsilon }_{t-3}+\text{0}\text{.9314}{\epsilon }_{t-4}\end{array}$ (11)

以第301天到第360天的动液面数据为对象，利用式(11)确定的模型，对其进行预测，其预测误差如图6所示。

由图6可以看出，使用ARMA法进行动液面的线性预测，其预测误差在 60 米 左右。虽然这种方法的预测值也能大体上跟随动液面时间变化的趋势，并且模型相对简单，计算方便，但是其预测误差还是较大的。

4.2. 最大Lyapunov指数预测

Lyapunov指数是一个描述系统轨道指数发散程度的量化值，正是这个特性使它成为混沌时间序列的重要预测参数。令 $Y_m$ 表示预测的中心点。在构造的相空间中， $Y_k$ 是 $Y_m$ 的最近邻点，这个距离记为 $d_m\left(0\right)$ ， ${\lambda }_1$ 为最大Lyapunov指数，则有：

$\{\begin{array}{l}{d}_m\left(0\right)=\underset{j}{\min }\Vert Y_m-Y_j\Vert =\Vert Y_m-Y_k\Vert \\ \Vert Y_m-Y_{m+1}\Vert =\Vert Y_k-Y_{k+1}\Vert {\text{e}}^{{\lambda }_1}\end{array}$ (12)

其中， $Y_j$ 为 $Y_m$ 的邻点，并且点 $Y_{m+1}$ 中唯一未知的 $x\left(t_{m+\text{1}}+\left(m-1\right)\tau \right)$ 为最后一个分量。因此， $x\left(t_{m+\text{1}}+\left(m-1\right)\tau \right)$ 是可以预测的，可以按式(12)来进行最大Lyapunov指数预测。

已经证明动液面时间序列具有混沌特性，因此可以使用混沌时间序列预测的方法对其进行预测。以油井的动液面历史数据作为研究对象，数据采集期为一年，每天对动液面高度进行一次测量。将测量得到的全部动液面数据分成两部分，第一部分用来构造训练样本集，以建立一个最大Lyapunov指数预测模型；第二部分动液面时间序列数据作为预测样本，用于对预测模型进行测试。最大Lyapunov指数预测模型的预测结果如图7所示。

由图7可以看出，采用最大Lyapunov指数的混沌时间序列预测方法得到的预测结果，可以比较好的跟踪真实值，尤其在动液面相对较稳定时候，预测精度较高。

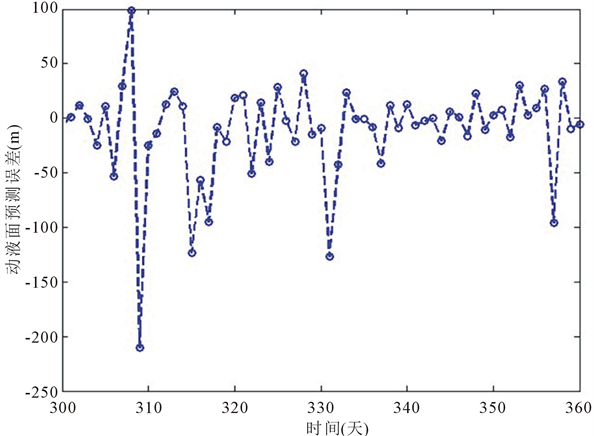
Figure 6. Error curve of forecasting value for producing fluid level

图6. ARMA法预测误差

Figure 7. Curves for producing fluid level forecasting

图7. 动液面高度预测曲线

4.3. 预测误差分析

为了定量的评价动液面时间序列的预测结果，我们使用以下四个误差指标进行考察：

1) 平均相对误差：

$\text{MAPE}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|\left(y_d\left(i\right)-y_t\left(i\right)\right)/y_t\left(i\right)\right|}\times 100\%$ (13)

2) 均方根误差：

$\text{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left[y_d\left(i\right)-y_t\left(i\right)\right]}^2}}$ (14)

Table 2. Errors analyze for producing fluid level forecasting

表2. 动液面预测误差分析

3) 平方和相对误差：

$\text{PERR}={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left[y_t\left(i\right)-y_d\left(i\right)\right]}^2}/{\displaystyle \underset{i=1}{\overset{n}{\sum }}{y}_t^2\left(i\right)}$ (15)

4) 相对误差在10%以内的后验概率，即 $\text{|}e\text{|}\le \text{10}\%$ 的后验概率：

$P_{\text{0}\text{.1}}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}I\left\{\left|\left(y_d\left(i\right)-y_t\left(i\right)\right)/y_t\left(i\right)\right|\le \text{0}\text{.1}\right\}}$ (16)

其中， $I\left\{A\right\}=\{\begin{array}{l}\begin{array}{cc}1& 若A为真\end{array}\\ \begin{array}{cc}0& 其他\end{array}\end{array}$ ，A表示相对误差在10%以内这一事件，n为预测样本总数， $y_t\left(i\right)$ 和 $y_d\left(i\right)$ 分别为潜油往复抽油机油井第i日的动液面高度的实际值和预测值。

表2中给出动液面预测误差评价指标的量化值，采用最大Lyapunov指数的混沌时间序列预测方法得到的动液面预测误差大大优于ARMA方法的预测误差。

5. 结论

本文首先对潜油柱塞泵的动液面时间序列的ARMA线性预测方法进行了研究。用此模型，对给定的样本进行动态测试，并给出了预测结果，发现ARMA线性方法在处理动液面预测问题上的效果并不是非常理想。针对动液面变化的混沌特性，使用混沌时间序列预测方法对动液面时间序列的预测问题进行了研究，建立了最大Lyapunov指数预测模型。本文最后，用4种误差量化指标定量地分析了两种模型的动液面预测效果。结果表明，使用混沌时间序列预测方法的预测效果更好。

基金项目

黑龙江省教育厅科学技术研究项目（12541156）。