1. 传统LDA + DMFT方法遇到的困难
从理论上预测晶体结构是凝聚态物理和材料科学中最基本的挑战之一,但是直到90年代对弱关联材料的第一性原理晶体结构预测才变得越来越精确。最近十多年,第一性原理晶体结构预测能力上的巨大进步,主要归功于固体材料复杂的总能表面中有效最小化算法的实现和密度函数理论(DFT)计算的高效实现。然而,由于密度泛函理论中采用的半局部近似方法,如局部密度近似(LDA)或广义梯度近似(GGA),无法准确预测许多关联电子材料的结构和基态性质,如莫特绝缘材料和关联金属等。研究结果表明,对这些关联电子材料的晶体结构和电子基态性质的预测由于DFT泛函不准确而跟实验结果有很大的偏差。然而,众所周知,DFT计算即使在获得完全错误的体系电子性质的情况下,也可以获得非常准确的体系总能量,譬如高温铜氧化物超导体中总能的计算。这是因为DFT的总能泛函是静态的,即总能对于电荷密度的一阶导数为零。因此,低能价电子密度的变化不会对总能造成很大的影响。尽管如此,LDA和GGA在预测很多关联材料的晶体结构时是错误的,譬如铈Ce,钚Pu和过渡金属氧化物(如FeO)等。当然,在另外一些关联材料中,当它们不是很接近局域态和巡游态的边界时,对DFT的扩展,如LDA + U和杂化泛函等在描述结构方面还是相当成功的,但这两种方法在体系接近局域–去局域转变点时都存在根本的困难从而使计算结果与实验结果不符,譬如对于铁基超导材料中氮族元素离铁原子平面的高度被DFT低估了0.15 Å。
为了超越DFT的半局域近似去解释材料中关联效应,人们发展了许多成熟的多体理论方法。其中最为成功的方法之一是密度泛函理论(DFT)与动力学平均场理论(DMFT)相结合的方法——DFT + DMFT方法 [1] [2] [3] 。在DMFT方法中也是基于关联的局域性,但仅仅对一个给定原子的关联局域性进行计算,它比DFT半局域近似方法中对三维空间一个给定点的局域性限制条件要宽松得多。LDA + DMFT方法对许多关联材料的计算获得了很大的成功,譬如SrVO3等。但它目前的应用主要是计算关联材料的电子结构性质,而对材料的结构优化没有很好的考虑进去。其原因主要是当前的LDA + DMFT方法的实现框架不是基于泛函的方法:它的实现首先是构建一个低能有效模型,然后采用DMFT自洽方法求解Hubbard类型的理论模型,这样就丧失了体系静态特性,从而导致总能精度的降低。总能的一阶导数将导致更大的误差,从而对原子受力不能进行准确的计算,最终导致对体系结构优化的失败。
2. 新的DFT + DMFT方法中对结构优化的实现
当前,在DFT + DMFT方法中,已经有两种计算力及结构优化的方法。其一来自Savrasov和Kotliar的工作 [4] 。在他们的理论中只考虑了DFT + DMFT泛函对原子位移的二阶导数,从而获得声子谱,进一步得到原子受力。此外,他们采用Hubbard-I杂质求解方法,忽略了在原子发生位移时DMFT自能的改变,这个改变实际上对原子受力有重要影响。其二来自Leonov等人的工作 [5] 。他们也提出了在DFT + DMFT中原子受力的计算方法,然而他们的计算不是基于静态泛函,而基于非静态泛函的DMFT总能导数在目前的计算条件下是难以精确计算的,对原子受力的计算也是不准确的,因此很难对体系进行准确的结构优化。因此对实际材料的结构优化中需要采取其他的方法。
最近几年,K. Haule等人通过将DFT和DMFT在统一的Luttinger-Ward泛函框架内进行考虑,开发了新的计算算法,即DFT + eDMFT方法,这一新的算法成功实现了对实际材料结构优化的高精度计算 [6] - [11] 。新的算法通过与连续时间量子蒙特卡罗(CTQMC)方法结合,使得原子受力可以收敛到比自由能本身更高的精度。这主要因为CTQMC方法中固有的统计噪声在计算原子受力时抵消非常准确,而在传统的QMC中是不可能准确地取样自由能泛函的相互作用部分(Baym-Kadanoff泛函F[G])。
3. DFT + eDMFT方法对原子受力的计算
晶体中作用在一个原子上的力定义为当一个原子或离子产生一个小的位移时,总自由能改变的负值。赫尔曼-费曼(Hellmann-Feynman)定理表明,这个力等于作用在原子核上的静电力,即HF力。但是由于实际计算中数值的离散化,以原子为中心的基矢或在原子为中心的投影方法中,作用在原子上的力还有一个附加的贡献,这个附加项通常被称为Pulay力。Pulay力包含来自于基函数导数的项,但不包含总能泛函关于格林函数或电荷密度的二阶导数。
静态泛函在电荷密度(格林函数)存在非常小的改变下,其值是不变的。实际上,如果泛函是精确的,我们可以在固定电荷密度的情况下考虑离子一个非常小的位移从而来计算其受力。此时,总自由能泛函G[G]的导数可以分为两项
(1)
第一项是在固定格林函数的情况下求自由能泛函对位移的导数,得到的力即HF力,第二项是在固定粒子位置的情况下,求自由能泛函对格林函数的偏导数。在动力学平均场理论中,自由能泛函最好采用Luttinger-Ward (LW)泛函G[G]
(2)
其中求迹计算包括空间自由度、自旋和松原频率。在固定离子位置时,LW泛函G[G]对格林函数一阶导数
等于
,由于Dyson方程此项变为零。因此离子受力依赖于其位置的项仅包含在G0和Enuclei中
(3)
其中T和Vnuclei分别是动能算符和核势能算符。由于Vnuclei是不依赖于频率的,在第一项中,我们用电荷密度代替格林函数对松原函数进行频率部分求迹
最终得到HF力
(4)
精确的Baym-Kadanoff泛函是所有骨架费曼图的求和,对实际的固体材料是不可能精确获得的。在DFT + eDMFT方法中,相互作用泛函F取下列近似
(5)
第一项和第二项给出了通常的DFT方程。第三项是对所有费曼图的求和,其中每一项局域在给定离子位置Rm处,它的形式和相互作用的精确泛函形式相同,只是其中的格林函数G用局域格林函数Gloc代替。局域格林函数Gloc利用量子蒙特卡罗方法通过安德森杂质模型获得(Gloc = Gimp)。最后一项是在DFT和DMFT中重复考虑的弱相互相作用部分,即双重统计部分,此项目前已经可以精确获得 [7] 。将此泛函代入自由能表达式,在选择适当的基矢后,利用自由能泛函的静态稳定特性,得到稳定点的格林函数G,再将G代回自由能泛函G(G),得到体系在基矢下系统的自由能F
(6)
为了得到原子的受力,我们需要考虑自由能F有一个小的变化
(7)
考虑到HF力(即方程(4))得到
(8)
其中
。此即晶体中离子所受合力,可以将其写为如下形式
(9)
从而得到一个原子上的Pulay力
(10)
方程(9)是在DFT + eDMFT方法中计算力的一般表达式,它是与基矢选择无关的,在具体实现时,我们需要选择适当的基矢进行计算。目前K. Haule等开发的软件包也可以在网上免费下载和使用 [12] ,其DFT部分采用基于全电子势的Wien2K软件包,新的DFT + eDMFT方法已经成功实现了对具体材料的计算,并得到了一些可以与实验可以比拟的结果。
4. DFT + eDMFT方法的应用实例
下面以铁基超导材料FeSe为例来对其进行结构优化。块体FeSe空间群为P4/nmm,其单胞包含4个原子:两个Fe原子和两个Se原子,Fe原子处于一个平面,而Se原子交错处于Fe原子平面上下,如图1左图所示。图中将Se原子离Fe原子平面的距离设为ZSe(采用约化坐标)。在FeSe体系中,Se原子的高度ZSe将严重的影响体系的电子性质。ZSe越大,Se原子和Fe原子之间的杂化越小,从而使Fe原子的局域关联越强,从而影响费米能级附近d电子能带,并进而影响其超导电性。通过DFT + eDMFT方法我们可以得到优化的ZSe值,结果如图1所示。从图1右可以看到,随着DMFT自恰循环次数的增加,Se原子受力和自由能最终都收敛达到一个稳定值。从图中我们还可以看到力的统计噪音要比自由能更小,因而Se原子受力达到一个更高的精度。此外,我们还计算了Se处于不同高度时的受力情况,计算结果如图2左所示。从图中可以看到Se原子受力随高度ZSe近似成线性关系,原子受力为零的平衡位置大概在ZSe = 0.27的位置。通过对原子受力进行积分得到的自由能数据,其统计误差要比通过自由能公式计算的统计误差更小。根据实验结果,FeSe中洪特耦合参数JH约为0.75eV,而ZSe~0.27。由于洪特耦合参数JH强烈的影响局域磁矩的涨落,并进一步影响电子的关联强度,从而影响FeSe体系的超导电性。因此,计算Se原子稳定位置ZSe与洪特耦合参数JH的变化关系,具有非常重要的意义。通过新方法计算的ZSe与JH关系的结果如图2右图所示。从图中可以看到,LDA和GGA计算给出的ZSe约为0.23到0.24,其结果明显的比实验结果低。而在新方法中,Se原子的稳定平衡位置处于0.26~0.29之间,明显的更接近实验结果 [10] 。
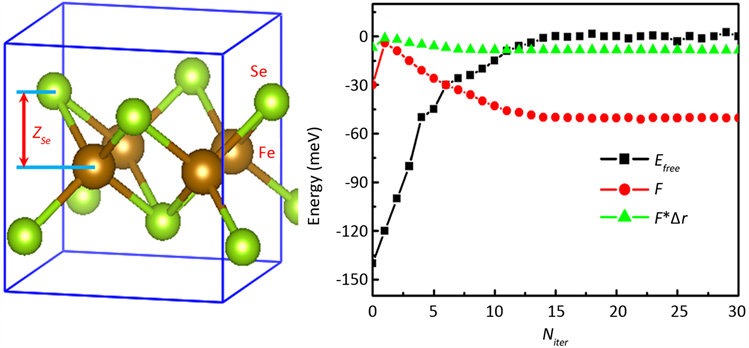
Figure 1. Left panel: Atomic structure of bulk FeSe. ZSe represents the height of Se atoms from the Fe plane; Right panel: force F on Se (red line), free energy Efree (black line), and force times displacement F*Dr (green line) as a function of iterations Niter of DMFT. We set ZSe=0.25 in our calculations
图1. 左图:FeSe晶体的原子结构图,Se原子离Fe原子平面的高度为ZSe;右图:Se原子受力F(红线),自由能Efree(黑线),受力与位移乘积F*Dr(绿线)随DMFT循环次数Niter的变化关系,其中ZSe=0.25
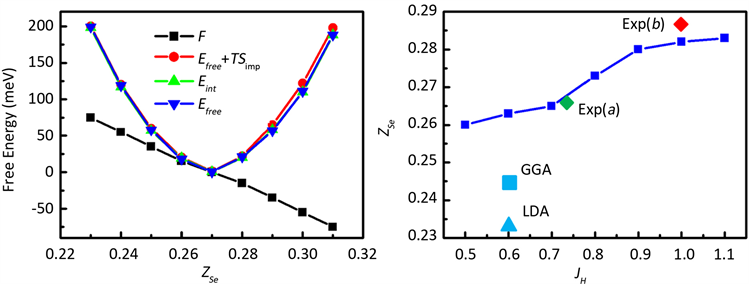
Figure 2. Left panel: force F on Se (black line), free energy Efree (blue line), free energy at finite temperature Efree + TSimp (red line), and integrated force (green line) as a function of ZSe. Right panel: the ZSe as a function of Hund coupling JH
图2. 左图:Se原子受力F(黑色),自由能Efree(蓝色),有限温度自由能Efree + TSimp (红色)与原子受力的积分(绿色)随ZSe的变化关系;右图:优化的ZSe随洪特耦合参数JH的变化关系
5. 结论
在本文中,我们介绍了一种在关联材料体系中实现结构优化的新算法,即DFT-eDMFT方法。新的算法最重要的特征是能够在Luttinger-Ward泛函的统一框架内实现DFT和DMFT的计算,并获得实际材料体系中离子受力,从而对体系结构进行优化。新算法把实空间DMFT费曼图直接嵌入到DFT的实空间泛函中,由此产生的总能泛函是静态稳定的,这种特性导致当一般的Dyson方程得到满足时,泛函dG[G]的变分为零。新的方法应用到实际的铁基超导材料FeSe中,通过结构优化获得的晶格常数要比LDA和GGA方法得到的结果更接近实验结果。新的方法实现了对一个单胞中所有离子受力的计算,从而实现了对关联电子材料结构的预测,这对于在有限温度下具有复杂相图的关联材料的电子结构计算具有很大的应用潜力。新的方法丰富了计算物理的内容,拓展了计算物理方法在关联材料体系中的应用范围,具有理论和实际的双重意义。
基金项目
《计算物理及其应用》国家精品资源共享课,计算物理国家教学团队,湘潭大学第八批教学改革研究项目:基于国家精品资源共享课建设视角的理工科专业创新型人才培养模式研究。