非晶合金与硅钢片高速永磁电机定子二维温度场对比分析

Analysis and Comparison of 2D Temperature between Amorphous Alloy and Silicon Steel Sheet of High-Speed Permanent Magnet Motor

摘要: 随着中国电机进入ie3时代，电机对效率的要求越来越高。非晶合金作为一种新兴材料，具有高磁导率、低损耗等特点，开始被应用于电机生产当中。然而非晶合金材料对机械应力敏感，因此设计了一种硅钢片与非晶合金相结合的新型定子结构。由于两种材料的损耗不同，温度也会有很大的影响；同时由于高速永磁电机其转速快、绕组电流频率高和磁场空间谐波频率大导致定子铁耗、转子护套与永磁体上涡流损耗以及风磨损耗相比于其他电机的损耗有大幅度的增加；相比而言其体积小，散热差，因此对于定子结构的局部温度的研究是必不可少的。本文对一台额定功率为8 kW，转速为24,000 rpm的新型结构非晶合金高速永磁电机的定子结构进行温度场计算与分析。采用二维有限元算法分别计算定子两种材料的铁耗分布，对其各个位置的散热、导热情况，结合水冷结构加以考虑，最后进行二维温度场稳态分析与计算，对两种材料的温度进行对比与分析。对于电机局部温度情况的掌握具有一定借鉴意义。

Abstract: With the motor into the ie4 era in China, the demand on the efficiency of motor is higher and higher. Amorphous alloy as a new material with high permeability and low loss characteristics has been applied in motor production. However, amorphous alloy material is sensitive to mechanical stress, therefore, a new stator structure combined with silicon steel sheet and amorphous alloy has been designed. Because different materials have different losses, the temperature of them will be changed obviously; in addition, due to the high speed, high frequency of the winding current and high frequency of the magnetic field space harmonic, the core and copper losses of stator, eddy current loss and air-friction loss of the rotor will be much more compared to the normal speed machine. In contrast, the volume of it is little. As a result, the research for the local temperature of the stator structure is indispensable. This paper focuses on the loss analysis and thermal calculation and analyzes a 7.5 kW, 36,000 rpm new amorphous alloy structure high-speed permanent-magnet motor. The core loss of two kinds of materials is analyzed based on the 2D finite element respectively. The temperature field is analyzed by 2D steady-state temperature field analysis. The heat dissipation and thermal conductivity of every location, combined with water cooling structure are considered. At last, the results obtained are compared and analyzed. At the same time, they have reference significance to the partial temperature of new stator structure motor.

1. 引言

近年来，高速电机因体积小，功率密度大，动态响应快等优点，逐渐在各种电机领域得到广泛的关注。但由于其转速快、绕组电流频率高以及空间磁场谐波含量高导致高速电机运行损耗过大，同时其体积小、散热性能差，因此高速电机的温度问题不可忽视；非晶合金，作为一种新型导磁材料，具有高磁导率、高饱和磁密、小矫顽力、低损耗等特点，在当今节能减排的大环境下引起了国内研究人员的关注，并开始将其应用于电机设计之中。因此非晶合金高速永磁电机凭借其材料独有的高效节能的特性，以及永磁电机多种场合适应性强的突出优势，在国内高速电机的研究中引起了高度的重视。国外早在1982年，美国通用电气公司(GE)首次采用非晶合金制作电机定子铁心，在研究的过程中发现样机定子铁耗降低了约80% [1] 。1994年，波兰学者Dems M.，Komeza K.，Wiak S.第一次提出非晶合金电机的概念 [2] 。为了更好地将非晶合金材料独一无二的优势特性运用在永磁电机的应用上，其他研究学者也做出一系列贡献 [3] [4] ；2013年，Dems M.和Komeza K.通过有限元计算和试验测量，对一个小型异步非晶合金电机的损耗和性能进行了验证，实验证明非晶合金电机可以显著降低定子铁心损耗，同时建议采用非晶合金制作转子，以降低转子损耗 [5] 。在温度场研究方面，1998年，芬兰赫尔辛基大学的Juha Saari采用热网络法对高速电机的温升进行分析计算，对转子风磨耗和涡流损耗对转子温升的影响做了大量分析 [6] 。2008年，Fodorean等人分别对三种不同保护套材料转子的温度场采取3D有限元法和等效热路法两种不同的算法进行分析，通过实验结果表明，有限元法计算更接近于实验数据 [7] ；目前国内非晶合金为定子材料的永磁电机已经陆续研发。朱龙飞以一台轴向磁通非晶合金永磁电机为例，采用对定子结构分为轭部与齿部空载铁耗进行了解析计算 [8] ，同时又基于Bertotti的三项式常系数模型，通过实际测量非晶合金电机，在频率范围为266.7 Hz到550 Hz以下的条件下，对磁滞系数进行了修正并进行了验证 [9] 。冷建伟使用ANSYS Maxwell软件对同样型号的传统电机与非晶合金电机的性能进行对比分析，但并没有考虑非晶合金材料在Bertotti三项式上常系数模型的适用性 [10] 。2015年，佟文明等人采用了正弦波电流、矢量控制、直接转矩控制三种运行方式下进行非晶合金永磁电机的铁耗研究，将定子分成轭部、齿身、齿跟与齿顶通过时步有限元进行运算 [11] 。在温度场方面中国也取得了重大进展。2007年，东南大学的黄云凯与悉尼理工大学的朱建国等人合作研究了20,000 rpm的爪极永磁电机空载时的温度场，其定子轭部的温度计算值与实测值误差在10%左右 [12] 。2008年，哈尔滨工业大学张洪亮、邹继斌、陈霞、江善林又采用二维有限元法对交流永磁同步电动机的定子温度场计算，进行进一步细化，综合考虑电机中交变与旋转磁场的影响，同时又计算了电机定子饱和铁心损耗与磁极涡流损耗，并将此计算结果应用于电机的三维温度场计算当中，但是对于转子的温度场模型处理，做了大量的忽略 [13] ；2013年，赵玫等人对横向磁场永磁直线电机进行了铁耗分析计算与三维温度场的计算，但是热源选取不够精细，并没有考虑机械损耗 [14] ；2015年，沈阳工业大学的刘光伟用三维有限元计算了一台高速永磁爪极电机的电磁场，不仅考虑了定子中的旋转磁化，高次谐波引起的损耗作为热源，同时对转子的粗糙度，转速所引起的风磨损耗加以考虑，不过并没有做相对应的温度场分析 [15] 。

基于以上研究背景，本文为了准确了解定子局部的温度情况，采取以磁密的大小、特性作为划分定子各部分提取生热率的方法。本文采用的两台仿真电机，在空载情况下运行，定子分别使用的是高频硅钢片与铁基非晶合金材料，计算铁芯损耗后，进行二者温度场的分析与计算。

2. 定子损耗计算

试验电机为高速永磁电机，永磁体为钕铁硼材料采用Halbach充磁，电机结构如图1，外径采用水冷结构，其他基本参数见表1。

在对于试验电机的定子结构，高速电机的谐波、旋转磁化和磁密分布不均匀等影响因素的存在，增加了铁耗的计算难度，为了准确测量定子结构各位置的温度，铁耗计算模型显得非常重要。由于电机定子的周向周期性结构，以电机的一个齿距的范围来进行磁场分析，即取1/24的结构模型，如图2(a)所示。对磁化更加严重，在磁密大小一样的交变和圆形旋转磁密，圆形旋转磁密所形成的损耗比交变磁密大很多，在磁密较小(小于1T)时，圆形旋转磁密损耗，差不多是两个正交方向单独有相同大小磁密的交变磁密产生的损耗之和。在磁密大于1T时，圆形旋转磁密损耗则小于两个正交方向单独有相同大小磁密的交变磁密产生的损耗之和 [8] ；其次在使用Maxwell可以更准确的提取热源也是问题的关键。

Figure 1. Section view of the stator

图1. 电机截面图

Table 1. Parameters of machine

表1. 电机参数

首先搭建2D模型，通过时步有限元对电机铁心磁场进行数值计算，以电机旋转360度电周期为一周期，由于是4极电机，即180度机械角度，进行磁场计算，可得到定子铁心每一个剖分单元磁密的径向分量与切向分量B_x、B_y。为了对定子进行合理的分块来求解各部分的铁耗值，并且使求解的铁耗作为热源更具有说服力，在这个1/24 的定子结构模型上的不同位置上选取32个点以便于进行磁密大小以及波形变化对比分析，其磁密点各个位置大致如图2(b)所示，并进行命名：由齿顶到轭部径向依次为A、B、C、D、E、F、G、H、I；周向由左向右依次为各点下角标1、2、3、4、5。

(a) (b)

Figure 2. 1/24 Stator structure and position of the measured magnetic flux density point

图2. 1/24定子结构与测量磁密点位置

通过Maxwell后处理可以求解各位置磁密的大小以及B_x、B_y，由于点数多，在此不一一列举如何进行径向、轴向比对，以非晶合金材料下定子的下列几种对比方案作为代表进行分析。在齿尖、齿顶中间、齿身中间、齿跟中间、轭部中央以及轭部底的中间选出各位置一点作为代表分析其旋转磁化特性，如图3所示，左侧红线为磁密y轴分量，蓝线为x轴分量，右侧图为磁密运动轨迹。通过对32个点位进行磁密的分析可知，从周向磁密的变化可以发现，齿身、轭部各位置的磁密幅值接近相等，并且齿尖、齿身与靠近定子外径的磁密旋转磁化非常小；齿顶位置的磁密幅值由中间到齿尖变大，并且旋转磁化变得很弱；齿跟处的磁密幅值变化也非常明显；从径向来看，磁密幅值由齿顶到齿轭依次变小，旋转磁化程度从齿顶到齿身逐渐变小，再到齿跟处达到最大，最后到齿轭部分渐渐减小，需要注意的是齿身与轭部的各个选取点的磁密幅值变化不明显，并且基本为交变磁化产生的磁密，在进行分块时可以径向进行大尺度分块。通过以上的磁密规律可以对其进行如图4所示的分块结构，并对各个分块进行磁密的平均值求取以便于后续铁耗计算的处理，同时作为处理热源的提取方法。

齿尖(A1) 齿顶(B2) 齿身中央(C2) 齿跟中间(E3) 轭部中央(G3) 槽底中间(G1)

Figure 3. The magnetic flux density waveform and Elliptic magnetization curve

图3. 磁密波形及椭圆磁化曲线

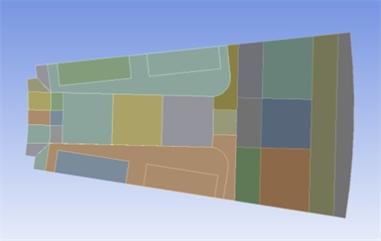
Figure 4. Block extraction model of heat source of stator

图4. 定子热源分块模型

在进行铁耗计算时，采用铁耗分离理论，使用传统铁耗两项式铁耗模型 [16] [17] ，

$P_{Fe}=K_{h}f{B}_n^{\alpha }+K_{e}f{B}_n^2$ (1)

式中：K_h磁滞损耗系数；K_e涡流损耗系数；f是铁芯中磁密基波的频率， $\alpha$ 为待定系数对通过实验测量的损耗值进行回归分析，可求其磁滞损耗的系数，由正交分解旋转磁化计算模型，可知适用于该非晶合金电机的变磁滞损耗计算模型为下式 [8] ，

$P_{Fe}=K_h{\displaystyle \underset{v=1}{\overset{\infty }{\sum }}vf\left(B_{v\max }^{\alpha }+B_{v\min }^{\alpha }\right)}+K_e{\displaystyle \underset{v=1}{\overset{\infty }{\sum }}{\left(vf\right)}^2\left(B_{v\max }^2+B_{v\min }^2\right)}$ (2)

式中：v为谐波次数；B_vmax和B_vmin分别为椭圆形旋转磁化长、短轴v次谐波磁密幅值。

通过计算，非晶合金铁心损耗为12.3 W，高频硅钢片铁芯损耗52.9 W，高频硅钢是非晶合金损耗的4倍多。

3. 温度场计算

本文建立了考虑水冷结构、机壳与定子二维温度场模型，以二维电磁场的计算结果作为热源进行耦合。由于电机周向结构的周期性，同时为了方便运算，并且节省计算机运行时间，仍然以1/24的模型，即15度的二维模型进行分析，如图5所示，其中满足绝热边界条件为：2、9槽楔截面；3、10槽内等效绝缘材料截面；4、11绕组截面；5、12定子截面；满足对流换热边界条件为：1、8槽楔表面；6定子外径与水接触面；7齿部表面。依据传热学理论，固体表面三类边界条件为

$\begin{array}{l}{T}_{S_1}=T_S\\ {-{\lambda }_n\frac{\partial }{n}|}_{S_2}=q_0\\ {-{\lambda }_n\frac{\partial }{n}|}_{S_1}=h\left(T-T_c\right)\end{array}\}$ (4)

式中：T为温度(℃)；T_S为已知壁面温度(℃)；T_c为周围介质的温度(℃)；q₀为通过边界面的热流密度(W/m³)，当q₀为0时S₂为绝热面；c为比热容(J/(kg·℃))；ρ为密度(kg/m³)；t为时间(s)；h为散热系数(W/(m²℃))；S_i(i =1, 2, 3)为第1类边界条件的物体边界；λ_n为边界面的法向导热系数(W/(m·℃))。因此，热平衡的微分表达式为

$\frac{\partial }{\partial x}\left({\lambda }_{xx}\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left({\lambda }_{yy}\frac{\partial T}{\partial y}\right)=q$ (5)

式中：λ_xx、λ_yy、λ_zz为各介质x、y、z方向的导热系数(W/(m·℃))；q为热源密(W/m³)。

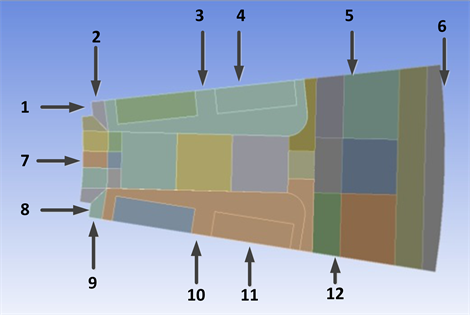
Figure 5. 2D temperature field model of stator

图5. 定子二维温度场模型

其假设条件如下：

1热源不随温度变化；

2材料特性不随温度改变；

3槽内绕组、槽内气隙与绝缘纸、定子轴向导热系数分别进行等效计算；

4铁心端面、槽绝缘端面及铁心外表面的散热系数取经验值。

3.1. 生热率的求取

通过2.1~2.2中对各部分损耗的求解，将结果当作热源作为温度场模型的热激励。其中定子铁心以齿尖、齿跟、齿身、齿顶、轭部的各个部分的热源见表2，其在生热率中的比重如图6。依据公式如下，

$q_s=P_{loss}/S$ (6)

式中： $q_s$ 、 $q_v$ 分别是面生热率与体生热率； $P_{loss}$ 是指损耗功率；S是生热面；V是生热体。

Table 2. Heat generation rate

表2. 生热率

通过表格数据可以发现，非晶合金生热率整体要远远小于硅钢片的生热率；同时，二者都是轭部损耗所占比重最大，非晶合金定子在齿根处的损耗占比要比高频硅钢的低。

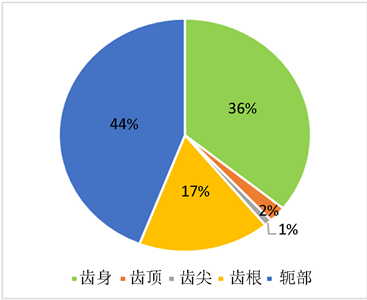高频硅钢片损耗所占比例 非晶合金损耗所占比例

Figure 6. The proportion of the two kinds of materials to the location of the heat generation rate

图6. 两种材料各位置损耗比重

3.2. 定子的散热与导热

在进行温度场计算，各个材料之间的导热性能以及材料与空气、水、气隙之间的散热不可忽视。同时，由于电机结构中存在很多混合材料，因此合理的进行等效计算是必要且可行的算法。本台电机的二维温度场模型如图7所示。定子径向等效传热系数的公式如下 [17]

${\lambda }_x={\lambda }_y=k_{Fe}{\lambda }_1+\left(1-k_{Fe}\right){\lambda }_0$ (7)

式中： $k_{Fe}$ 为定子的叠压系数，其中硅钢片为0.96，非晶合金为0.93； ${\lambda }_1$ 是定子铁心材料的导热系数； $$ 是定子叠片中绝缘材料的导热系数。因为绝缘材料与定子铁心材料的导热系数相差甚远，通过上式可以发现，绝缘材料在定子径向传热上基本没有影响，为了简化计算可以忽略。

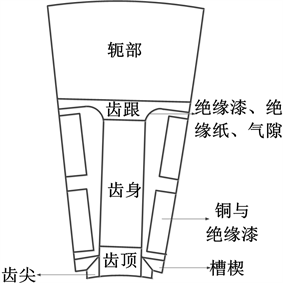
Figure 7. Curve: system result of standard experiment

图7. 定子二维温度场简化模型

在定子槽内的导热系数确定中，由于槽内的材料的多样性，为了求解温度场更加精准，其导热系数也是需要进行重新等效的。其中槽内绕组等效传热系数的选择为如下经验公式 [17]

${\lambda }_R=\frac{\left({\delta }_{cu}+{\delta }_j\right){\lambda }_{cu}{\lambda }_j}{{\delta }_{cu}{\lambda }_j+{\delta }_j{\lambda }_{cu}}$ (8)

式中： ${\delta }_{cu}$ 、 ${\lambda }_{cu}$ 分别是铜裸线的等效直径与导热系数； ${\lambda }_j$ 、 ${\delta }_j$ 分别是绝缘材料的等效厚度与导热系数，之所以选择上述经验公式，是因为本电机采用下线方式如图，上述公式更适合将铜导线、绝缘漆以及残余空气的导热系数一并考虑在内。槽内除此以外还有起封盖定子槽口的作用的槽楔，本实验电机的定子槽楔采用环氧树脂灌封胶，其导热系数为1.3(W/(m·℃))，其散热系数可通过绝缘表面散热公式求解 [18]

${\alpha }_j=\frac{1+\sqrt{\omega r}}{60000}\times {10}^6$ (9)

式中：ω转子角速度；r是转子外径。

另外，定子齿部的散热系数由以下方程确定 [17] ，

$\begin{array}{l}{\alpha }_c=28\left(1+v_{\delta }^{0.5}\right)\\ v_{\delta }=\frac{1}{2}\omega r\end{array}\}$ (10)

3.3. 水路结构的散热特性

对于水路冷却结构如图8所示，根据热力学定律，定子外径以及机壳与水流之间存在强制对流换热，系数为 [19] ，

${\alpha }_w=\frac{N_u{\lambda }_w}{d_h}$ (11)

式中：N_u为努塞尔数，体现流体的换热特性； ${\lambda }_w$ 是水的导热系数；d_h为当量直径，其公式如下，

(a) 水路结构 (b) 水路结构截面图

Figure 8. Water cooling structure

图8. 水冷结构

$d_h=\frac{4A}{U}$ (12)

式中：A为流体流过的截面积；U为润湿周长。努塞尔数在流体为紊流条件下，下式计算 [19] ，

$N_u=0.12\left(R_e^{0.87}-280\right)P_r^{0.4}\times \left[1+{\left(d/L\right)}^{2/3}\right]\times {\left(P_r/P_w\right)}^{0.11}$ (13)

式中：R_e为雷诺数；P_r为常温下的普朗特系数；L是水路长度；P_w是流体在壁温下的普朗特系数。上述公式中相关参数可以通过相似理论和水路特性求取 [19] ，

$\begin{array}{l}{R}_e={\rho }_W{v}_w{d}_h/u\\ P_r=\frac{u{c}_P}{{\lambda }_W}\end{array}\}$ (14)

式中： ${\rho }_W$ 是水流体的密度；v_w是水的流速；c_P是恒压比热容。最终求取水对机壳的散热系数为1853.19 (W/m²·℃)。

Table 3. System resulting data of standard experiment

表3. 各材料导热系数

4. 温度场结果与分析

各种材料的导热系数见表3。仿真假设室温22摄氏度，电机内部温度为30摄氏度，水温为20摄氏度，水流速度为0.2 m/s，按2、3章计算的热源结果、散热系数、导热系数分别对应模型相应位置进行设置，其剖分情况见模型如图9所示，最终在Workbench中得到空载情况下的温度结果如图10、图11所示。

Figure 9. Meshed Temperature field model

图9. 温度场剖分模型

由计算结果可知两种材料定子最高温度在齿身靠近齿根处；各个位置非晶合金温度都低于硅钢片。由于有水冷散热，定子外表面温度相对低。

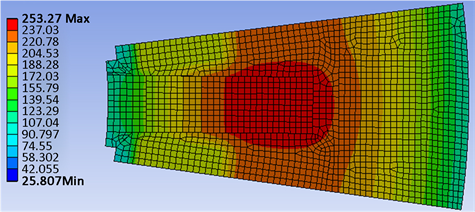
Figure 10. Temperature distribution of silicon steel sheet

图10. 硅钢片温度分布情况

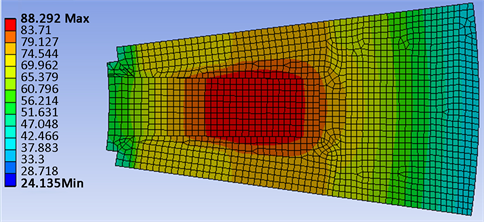
Figure 11. Temperature distribution of amorphous alloy

图11. 非晶合金温度分布情况

5. 结论

本文分别针对硅钢片与非晶合金电机进行了时步有限元的二维瞬态场的电磁场计算和二维稳态温度场的计算，并且为了得到更加确定的局部温度，不仅以定子不同区域作为提取热源的分块，而且以各位置的磁密幅值及其磁化程度进行分块，进行电磁场与温度场的耦合。经过耦合计算后，对两种材料热平衡下的局部温度有了一定的认识：

1) 由于高平硅钢片的铁损是非晶合金的4倍多，硅钢片定子的各个位置的温度都高于非晶合金。

2) 外加水冷散热效果明显。

3) 两种材料的最高温度都发生在齿顶部位，因此在实验时应更加关注定子齿部的温度变化；综上所述，在对定子温度进行检测时应关注定子齿根的温度变化。由于本文未搭建试验平台进行实验，无法计算结果的准确度。

同时，本文未搭建试验平台进行实验，无法计算结果的准确度；此外，由于二维电磁场没有考虑端部效应，二维温度场中也无法考虑到轴向的温差，因此存在着一定的误差，需要在今后的三维场中加以分析。