1. 奇合数体的表示法
设p是素数,Q与q是奇数,使
[1] ,若
,
,
,
,
,则有
,从而
。N称为奇合数体,可得定义1,奇合数体的表示法,
(1)
2. 命题证明
用反证法,假设存在奇完全数Q,
,
,p是奇完全数Q的素数因子,
,把Q分为两个奇数的乘积,
,根据奇完全数的定义,有
,
。
设,
,则有
。
即:
可得:
(2)
(2)式称为奇完全数的奇体表达式。由(2)可得推论一,N为偶数,t也是偶数。
证:若N为奇数,则
为奇数,而
为偶数,左右奇偶不合,故知
必为偶数,
是奇数,所以t必须是偶数。证明完。
,根据定义1,
,(
,
)。
在
中,设
是Q中最小的素数,把
及
分别表为
,
可以依据组合
的不同,形成不同表达式。
将各种组合代入(2),有
上式简化后得:
(3)
要使(3)成立,必须满足
[2] 。
我们可以得到推论二,在
中,
或
,两者必取其一。
证,
,即:
,其中
和
可以表示为
,
证明完。
我们讨论当
时,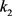 的取值。
的取值。
把
和
还原为Q,
,
,
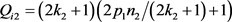 ,
是奇数,
应该是偶数,要使
,
是奇数,
应该是偶数,要使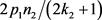 是偶数,必须满足以下条件:1)
,有
, 2)
有
,3)
有
:
是偶数,必须满足以下条件:1)
,有
, 2)
有
,3)
有
:
1)
,
不是整数,
当
时,
。
因此我们可以得到推论三,在
中,有
,即
。
证,如果
,则有
,使得
.,与推论三矛盾。证明完
2)
,即
,使等式成立。
t是偶数,设
,
,满足等式,
,这样的结果与
相同,
,
3) 在
中,
不是整数,
必须是整数。
是Q中最小的素数,
,
,
可以表示为
,
,
,
是Q中的素数。
,
,
,
设
,
,有
,显然
,
(3)有:
,即
,
不是整数,
必须是整数,如果.
是整数,即
,
(2)有:
使得
。
,即
,
不是整数
,即
。
,用Q中
逐个代入
,这使得
。
。
,
,
不是整数,
必须是整数,
在能整除
的同时,
还必须整除
。
,这样便造成
,
当
时,因
无法取值,原假设不成立,所以不存在奇完全数。证明完!
NOTES
作者简介:出生年月:1959年9月,籍贯:广东省始兴县,学历:本科,职称:工程师。