基于立方体网格插值算法的气象雷达数据的三维重建

3D Reconstruction of Meteorological Radar Data Based on Cubic Grid Interpolation Algorithm

摘要: 在气象领域中，气象目标在整个探测范围内具有数目多、区域散、面积小、形状不规则等特征，使用常规插值算法重构的三维云层图易造成图像信息准确性不高，离散或体积较小的目标信息丢失等问题，使得重建的三维图像常常不能满足实时业务的需求。本文根据雷达实际观测数据，提出并实现了一种立方体网格插值算法，将不规则的雷达锥面数据映射到规则的三维数据场中，并结合Marching Cubes算法对气象雷达数据进行三维重建实验。实验结果表明，使用本文提出的算法得到的三维重建云层图能较为准确地反映出气象目标的基本特征及其空间分布，满足气象业务需要，为气象目标实时跟踪和准确预报提供了参考依据。

Abstract: In the meteorological field, meteorological objects have many targets, scattered regions, small areas, and irregular shapes in the whole detection range. Using conventional interpolation algorithms to reconstruct three-dimensional cloud image may result in low accuracy of image information and discrete and small object image information loss which makes the reconstructed three-dimensional cloud image data often not to meet the needs of real-time business. Based on the actual observation data of radar, this paper proposes and implements a cubic grid interpolation algorithm, which maps the irregular radar cone data into the regular 3D data field, and combines the Marching Cubes algorithm to perform 3D reconstruction experiments on meteorological radar data. The experimental results show that the 3D reconstruction cloud map obtained by the proposed algorithm can accurately reflect the basic characteristics and spatial distribution of meteorological targets, which meet the meteorological service requirements, and provide a reference for real-time tracking and accurate prediction of meteorological targets.

1. 引言

在气象领域，常用多普勒气象雷达来探测降水的各项指标。气象雷达采集的数据为雷达回波的强度值，它在气象领域是一种常规的观测数据。气象雷达数据的三维成像是以气象雷达观测的回波强度数据为基础的三维重建，重建结果能使某一时刻气象目标的分布和形态变得形象直观，使气象工作者能深入理解和分析气象雷达数据，从而提升对复杂气象状况的预测能力。

三维成像在医学图像处理、计算机视觉等方面有着较为广泛和成熟的应用，但在气象领域，大多数研究都是集中在利用真实感技术对云层进行模拟绘制方面，而利用雷达数据进行云层重建的工作不多，主要原因是由于气象目标在整个探测范围内具有目标多、区域散、面积小、形状不规则等特征，造成重建图像准确性不高，容易使离散的、体积较小的目标信息丢失，或因人为增加数据点而导致计算量偏大等问题，所以我国大多数气象雷达回波产品都以二维形式展示。

近年来，国内外学者对气象雷达数据的三维重建都进行了较为深入的研究。就国外来说，Ernvik [1] 在其发表的文章中探讨了天气雷达利用三维可视化方法进行云层成像的初步研究结果。Ru [2] 对气象数据做了拼接处理后再对云层实现立体可视化。Denham [3] 使用了一种显卡并行处理技术对气象雷达数据进行处理，并对该方法其进行了优化，进一步提高了对气象雷达数据的处理速度。在国内，王轩 [4] 针对气象雷达基数据的空间特征，划分其为雷达投影面空间和雷达立体空间，对这两种雷达空间构建点阵模型，为气象雷达信息的多维表达和分析算法提供了模型支撑。刘岩 [5] 结合天气雷达数据三维空间定位公式与任意基线雷达反射率因子垂直剖面算法，提出了一种三维可视化的改进算法，并在此基础上研发了天气雷达数据三维显示系统。路明月 [6] 提出了一种新的面向web三维应用的气象雷达矢量剖面生成方法，使得对气象雷达矢量剖面的分析更加精确有效。

本文在前人研究的基础上，考虑气象雷达的探测角度一般在0.5˚至19.5˚之间，其观测数据分布不均匀且位于锥面上，为了使其与MC三维重建算法相匹配，必须采用适当的插值算法，将不规则的雷达锥面数据映射到规则的三维数据场中。常规的插值方法所处理的数据多为矩阵形式的规则数据，而锥面上的气象目标并非处在同一海拔高度上，若直接对锥面数据进行插值，其重构结果与真实云层之间就会形成较大偏差。

本文首先对锥面上的气象雷达回波数据分布特征进行分析，提出一种立方体网格插值算法，将锥体数据嵌入到预先定义的单位立方体中，建立三维数据场；之后使用Marching Cubes算法对气象雷达数据进行重建。重建结果表明，本文方法得到的三维回波图可以直观地展示云层的基本轮廓及其空间分布，有助于气象工作者对气象雷达回波强度信息进行分析，为气象预报及分析提供有力参考依据。

2. 方法描述

气象雷达扫描最主要的方式是体扫描。气象雷达在一个时次内对多个不同的仰角依次进行扫描，然后将不同观测仰角的数据排列在一起，构成一组气象雷达体扫数据。图1为雷达体扫描的示意图。

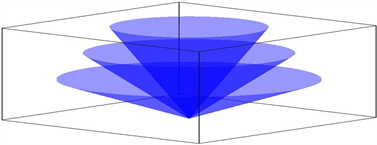
Figure 1. Volume scanning diagram of meteorological radar

图1. 气象雷达体扫描示意图

获取气象雷达的空间锥面数据后，首先需要对该数据进行空间的插值。由于常规插值方法无法实现将锥面数据映射到三维网格上，本文提出一种立方体网格插值算法。该算法首先将包含某一时次获取的雷达锥面数据嵌入到标准立体网格中，锥顶与网格底面中心对齐，使得每个单位立方体内都包含一定数量的锥面数据点，然后对每个立方体网格点的回波强度值与该顶点相邻的八个单位立方体内数据点的回波强度值进行加权计算。

(a) (b)

Figure 2. Radar echo intensity plane and the corresponding conical figure with a radar observation angle of 0.5 degree

图2. 某观测角为0.5˚的雷达回波强度平面图及其锥面图

2.1. 构建雷达锥体模型

为了直观地展示出雷达回波数据在实际空间中的分布，我们先利用纹理映射技术将雷达回波平面图映射到雷达锥体模型，即将多个气象雷达回波图作为纹理图像映射到同一个气象雷达锥体模型上。

我们选取昆明市某气象雷达站2014年6月6日0时0分采集的一个周期14个不同仰角的体扫描数据，单个仰角雷达体扫数据对应的回波强度图如图2(a)所示，图像中心就是雷达所在位置。采用纹理映射，将单个回波强度图映射到锥面，如图2(b)所示。

将所有仰角的锥面图叠加构成雷达锥体模型，如图3所示。从雷达锥体数据图看出，气象回波强度图的分布尺度不一致，并表现为明显的分层现象，且数据分布主要集中在靠近雷达中心的地方，远离雷达中心的地方，回波强度数据分布较少。随着仰角的增加，雷达所观测到的气象回波强度数据也逐渐减少。

Figure 3. Radar data cone model

图3. 雷达数据锥体模型

2.2. 立方体网格插值算法

采样数据在现实空间中是以14个锥面的形式分布的，数据样点的分布是不规则、不均匀的。为减少重构误差，本文提出以单位立方体为基础的空间插值与补盲方法，并将该方法命名为立方体网格插值算法(Cubic Grid Interpolation，简称CGI)。该算法的基本思想是：在锥面数据空间中构造一个包含该数据的标准网格，每个网格点的回波强度值用与该顶点相邻的八个单位立方体内采样点的回波强度值进行加权计算，如图4所示。

以图5单位立方体为例，需要求插值D点的回波强度值，只需确定以D点为球心、立方体边长为半径的球的内部所有原始数据，以这些数据到D点的距离函数来确定权值，如图6所示。

D点的回波强度来自于以该点为公共点的八个立方体内数据采样点的回波强度的加权值。实际上所有有效的数据采样点在以D点为球心、半径为R的球体内，D的回波强度值为计算该球体内所有采集点的气象回波强度值的加权平均值。

设d(x, y, z)为三维网格上顶点的回波强度值，则该顶点的值可用与该顶点相邻的八个单位立方体内采样点的回波强度进行加权计算得到。

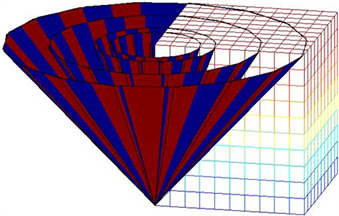
Figure 4. Embedding conical data into cube mesh figure

图4. 锥面数据嵌入立方体网格示意图

Figure 5. Interpolation point D and unit cube Diagram

图5. 插值点D与单位立方体示意图

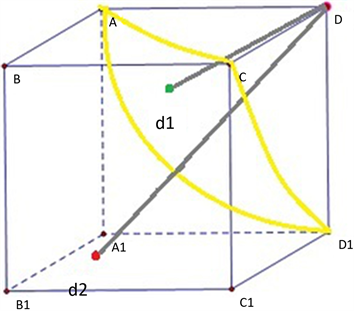
Figure 6. The relation between interpolation point D and sampling Points

图6. 插值点D与采样点的关系

$d\left(x,y,z\right)=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left[q\left(i\right)\times d_i\left(x_i,y_i,z_i\right)\right]}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}q\left(i\right)}}$ (1)

其中， $q\left(i\right)$ 表示赋予不同采样点的权值，最小值为0，当 $q\left(i\right)$ 计算结果为负数时，以0替代。而n表示D点相邻八个单位立方体中的数据采样点个数，n为非负整数。当n > 0时表示D点相邻八个单位立方体中存在数据采样点，可以通过取加权平均来计算 点的值；当n = 0时，公式(1)无意义，此时D处的值为空，可用一个非正常范围的数据常量进行填补，作为占位符，方便后面进行修补。

其中：

$q\left(i\right)=\frac{1}{\Delta l^{\lambda }}-1,\left(\lambda >0\right)$ (2)

λ是一个与权值分配有关的参数，Δl表示采样点与标准立方体顶点D之间的距离。λ决定了权值分配与Δl之间的联系。本文中取λ = 1，当λ = 1时，权值大小与Δl之间存在反比关系。

$\Delta l=\sqrt{\Delta x^2+\Delta y^2+\Delta z^2}$ (3)

通过 $x,y,z$ 分别向上和向下取整的排列组合，可以快速得到与该数据采样点相关的标准立方体的八个顶点的坐标，进而将该采样点d_i的回波强度按照权重规则赋予这八个顶点。

在上一步骤数据处理过程中，可能会出现以下两种情况：

一是在远离雷达处，数据样点稀疏，会出现公式(1)中n = 0的情况，存在无法进行数据估算的真空点；

二是靠近雷达处，数据样点密集，大量数据分摊权值，虽然有助于抵消异常值，但是关键数据的影响力被减弱，估算结果会被均衡化，无法充分体现特征。

为了解决以上两种情况所带来的问题，本文采用了改变估算网格点数据的球体半径的方法。我们在标准网格点构造中，以1 km作为D点的球体空间半径，增大球体半径，可降低出现情况一所带来的问题；减小球体半径，可以初步解决情况二所带来的问题。

具体操作方法是对 $d_i\left(x_i,y_i,z_i\right)$ 中现实空间的坐标轴做缩放操作，当坐标 $\left(x_i,y_i,z_i\right)$ 变成原来的一半时，所建立的网格节点间距变为2 km，此时D点的数据的球体半径也变为2 km，球体内数据样点增多，解决了出现情况一所带来的问题。虽然网格密度降低了一半，但可利用线性插值补足节点，恢复网格密度，这样得到的是精度为2 km的网格，将此种网格数据记作 $d_{2\text{km}}\left(x,y,z\right)$ ，而原来的标准网格记作 $d_{1\text{km}}\left(x,y,z\right)$ 。利用类似的方法，将坐标 $\left(x_i,y_i,z_i\right)$ 变成 $2\times \left(x_i,y_i,z_i\right)$ 时，网格节点间距离变为0.5 km，网格密度变成原来的2倍，此时只需提取处于偶数位置的网格节点作为目标网格即可恢复原来的网格密度，这样便解决了情况二所带来的问题。

因此修正后的网格数据是由 $d_{\text{0}\text{.5}\text{km}}\left(x,y,z\right)$ 先填充，剩余数据真空点由 $d_{1\text{km}}\left(x,y,z\right)$ 填充，再剩余的数据真空点由 $d_{2\text{km}}\left(x,y,z\right)$ 进一步填充，最终得到复合网格数据 $d\left(x,y,z\right)$ 。

综合上述，CGI算法流程如图7所示。

2.3. 结合MC算法实现三维重建

利用CGI方法可将14个锥面数据转换为20层等间距的平面数据，从而形成三维数据场，如图8所示。

在雷达数据三维重建过程中，我们选择Marching Cubes (MC)算法进行重建。MC算法是由William E. Lorensen和Harvey E. Cline提出，该算法的本质是对三维数据场中相同数值部分进行抽离，并通过三角面片拟合物体表面。

应用MC算法对雷达数据场进行三维重建，重建结果如图9所示。

Figure 7. CGI algorithm flow chart

图7. CGI算法流程示意图

Figure 8. Three-dimensional radar data field

图8. 雷达三维数据场示意图

Figure 9. 3-D reconstructed cloud results

图9. 三维重建云层结果示意图

3. 实验结果分析

为了验证本文方法的有效性，我们又以云南省气象台提供的昆明站2014年6月6日0时采集的气象雷达数据为例，分别进行了如下实验：利用CGI算法并结合MC对不同回波强度、不同剖面、不同时刻的气象雷达数据进行三维重建，并给出重建结果展示。

① 不同回波强度值的重建结果

回波强度是反映大气目标降水强弱的重要指标，数据单位以dBZ表示。我们取0时0分且高度为7 km时的云层数据，强度值分别为大于0、20、40、60的气象雷达数据进行三维重建，重建结果如图10所示。

(a) Echo intensity value ≥ 0 dBZ(b) Echo intensity value ≥ 20 dBZ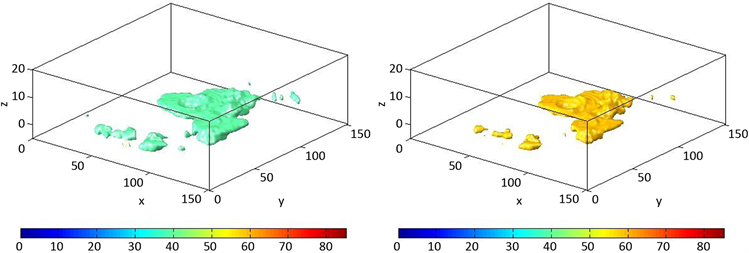(c) Echo intensity value ≥ 40 dB Z(d) Echo intensity value ≥ 60 dBZ

Figure 10. Reconstruction results of different echo intensity values

图10. 不同回波强度值的重建结果

② 不同剖面的重建结果

不同高度的水平剖面图可以看出降水区域大小，而垂直剖面图可以反映出降水云层的厚度和降水强弱。我们取0时0分且高度分别为2 km、4 km的数据进行重建，水平剖面重建结果如图11(a)，图11(b)所示，垂直剖分重建结果如图11(c)，图11(d)所示。

③ 不同时刻的重建结果

为表现重构后云图的真实感效果，我们选取00:00，00:59，01:59，02:58四个时刻的数据，并使用MATLAB三维渲染工具，对重构的云层进行真实感渲染，渲染结果如图12所示。

(a) Height =2 km (b) Height = 4 km(c) YOZ平面垂直剖分 (d) XOZ平面垂直剖分

Figure 11. Reconstruction results of different sections

图11. 不同剖面的重建结果

(a) 00:00时刻 (b) 00:59时刻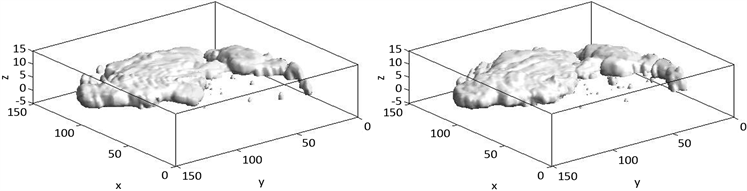(c) 01:59时刻 (d) 02:58时刻

Figure 12. Reconstruction and rendering results at different times

图12. 不同时刻的重建及渲染结果

由图可以看出重构后的云层图像能直观地展示出云层的基本轮廓，若将其与相关地理位置信息相结合，可以反映出该地区云层的空间分布，根据其位移变化可判断云层的运动方向，为气象预报及分析提供重要的参考依据。

4. 总结

本文首先利用纹理映射方法将气象回波强度数据映射到雷达锥面上，直观地展示出气象雷达回波数据的分布规律；再根据雷达锥面上气象回波数据的分布，采用一种基于立方体网格插值算法将锥体上的空间数据转换到三维规则网格上，建立了三维数据场；最后使用Marching Cubes算法实现了气象雷达数据的三维重建。重建结果表明，本文方法能够实现不同回波强度、不同剖面以及不同时刻的气象雷达数据的三维重建，为气象预测与分析奠定了基础。

致谢

感谢云南省气象台张杰高级工程师的精心指导。

基金项目

本文获得国家自然科学基金(11161055)资助。