1. 引言
在目前众多的研究领域中,经常会出现无回答的调查,这就不可避免的会带来数据缺失。数据缺失不仅会给分析数据带来一定的困扰,也会给分析结果带来偏差。
目前国内的大多数心理学期刊并没有对缺失数据如何处理给出明确的要求,但杂志社对文章质量的要求越来越高,当下一些国际性的心理学期刊对缺失数据的处理要求必须给出详细的说明,另外随着国内心理学研究与国际逐渐接轨融合,对于缺失数据的处理要求也会越来越严格,因此,如何减少或者消除缺失数据带来的偏差变得越来越重要,对缺失数据的研究也越来越受到研究者的重视。
2. 数据缺失机制
在处理缺失数据之前,我们需要知道数据缺失的机制,不同的缺失机制对应不同的分析方法,了解这些信息后才能选择恰当的方法来处理缺失数据。
在缺失数据的处理中,数据缺失机制的作用被研究者们长期的忽略,直到1976年Robin博士才给出明确的说明,他把缺失机制划分为三类(Rubin, 1976):随机缺失(Missing at Random, MAR)、完全随机缺失(Missing Completely at Radom, MCAR)、完全非随机缺失(Not Missing at Random, NMAR)。
我们用p表示概率分布,R代表缺失数据指标,Yobs和Ymiss分别表示数据集中实际观测到的部分以及缺失的部分,Φ是反映R与数据之间关系的一个参数。
1) 完全随机缺失。MCAR缺失要求变量Y上数据缺失的概率与其他观测变量无关,也与Y本身的值无关,用公式表示为p(R|φ) (Rubin, 1976)。这种缺失机制下数据缺失是完全随机的行为,其丢失的概率是未知的,换言之数据发生缺失与否与变量的取值没有任何关系。
2) 随机缺失。MAR缺失是指数据的缺失取决于数据集中其他变量,与自身取值没有关系,用公式表示为p(R|Yobs, φ) (Rubin, 1976)。
3) 完全非随机缺失。NMAR缺失是指数据是否缺失与数据集中其它变量的取值没有关系,只与缺失变量自身的取值有关,用公式表示为p(R|Yobs, Ymis, φ) (Rubin, 1976)。
不同的缺失值机制意味着需要采用不同的处理方法。NMAR与MAR和MCAR的情况不同,因此下面讨论的方法主要集中在MAR和MCAR两种条件下,NMAR的处理方法可参见Enders的文章(Enders, 2010)。
Enders曾以下面以一组数据对缺失数据的三种机制做了的介绍(Enders, 2010)。
例如在一次测试中,要求IQ达到88分以上才能参加随后的人格测验,这样IQ分数为78、84、84、85和87的数据便缺失了。这种数据缺失与人格变量自身无关,但却与IQ有关,称为随机缺失MAR。
完全随机缺失MCAR情况下数据缺失是随机的,不符合任何规律。换句话说,变量缺失值的出现完全是个随机事件,例如下表中IQ为78、84、96、112和134上数据的缺失,称为完全随机缺失MCAR。
完全非随机缺失NMAR数据缺失与其他变量无关,与自身表现得分相关。例如在表1中,公司新录用了14名员工,其中5名员工由于表现较差,在试用期内被辞退,年终表现评定中,被辞退的5名员工的表现分缺失了,这种情况下的数据缺失即为完全非随机缺失NMAR。

Table 1. Job performance evaluation for missing values of MCAR, MAR and NMAR
表1. MCAR、MAR和NMAR缺失值时的工作绩效评估
3. 针对缺失数据的处理方法
对于如何有效处理缺失数据,现有的方法大致分为以下几种。
3.1. 删除法
不考虑缺失数据的影响,直接在目前获取的数据基础之上进行分析。主要包括列表删除和成对删除。到目前为止,在社会和行为科学的许多领域中,列表删除和成对删除是最常见的缺失数据处理方法(Peugh & Enders, 2004)。
3.1.1. 列表删除(Listwise Deletion)
列表删除(也称为完全案例分析)把何缺少一个或多个值的案例的数据舍弃(Enders, 2010)。这种方法将分析限制在完整的案例中,不需要专门的软件和复杂的处理技术,最大的优点在于方便快捷。但是列表删除的主要问题是,它需要MCAR数据,当这个假设不成立时,会产生失真的参数估计(Enders, 2010)。此外,撇开参数估计失真不谈,采用列表删除会放弃相当数量的信息,带来大量有效资源的浪费。
对于如何评价列表删除,研究者们有不同的看法。也有研究者发现,如果缺失是预测变量而不是结果变量,那么列表删除可以在任何缺失数据机制下产生对回归斜率的无偏估计(Little, 1992)。Schafer和Graham认为很多场合下成列删除都是可取的,特别是当缺失比例很小的时候,个案剔除法拥有很高的效率(Schafer & Graham, 2002)。
3.1.2. 成对删除(Pairwise Deletion)
成对删除指如果配对的两个变量之一或者两个都是缺失值时,将其同时删除后再进行分析。与列表删除相一致,成对删除的主要问题是需要MCAR数据,当这个假设不成立时,也会产生失真的参数估计(Enders, 2010)。
所以可以发现,列表删除和成对删除不是不可取,如果缺失机制是完全随机MCAR,则删除后的数据计算的大部分统计量是无偏的。但是如果数据缺失不是完全随机的,是随机缺失MAR或者完全非随机缺失NMAR,删除后计算的所有估计值几乎都是有偏的。此外,如果数据缺失比例很小,列表删除和成对删除不会损失太多信息,在满足MCAR机制下对大部分统计量计算是无偏的,在这种情况下删除法也是一种可行的方法。
3.2. 基于插补的技术
很多情况下简单的将数据删除并不是好的方法,替换缺失数据,对缺失数据进行插补相比直接删除浪费更少的信息。插补的基本思想是对缺失值进行预测,用预测然后用这个预测值来代替缺失值,从而使缺失数据变得完整。
3.2.1. 单一插补
根据缺失值的插补值个数,插补方法可以分为单一插补和多重插补。单一插补是指为每一个缺失值只插入一个值。此外,根据插补模型的明确性,单一插补又可分为两类。第一类是基于明确的假设和模型进行插补,包含均值插补、回归插补、随机插补等。第二类在没有明确的假设和模型下进行插补,包含冷平台插补、热平台插补,最近邻插补等。
1) 均值插补(Mean Imputation)
均值插补用样本观测数据的均值去去填补该变量的缺失值。一般操作过程是当变量服从或近似服从正态分布时,可把此变量的平均值作为其所有缺失值的插补值;当变量服从偏态分布时,那么可考虑中位数或众数作为插补值(任志伟,2013)。均值插补不需要删除数据,保留了与缺失变量无关的其他信息,最大程度上的保证了数据的真实性与完整性。但是同一个变量中的缺失值都用同一个均值来替换,会严重扭曲了样本的分布。这种方法会产生估计误(Little & Rubin, 2014)。也最不为方法学者推荐(Allison, 2003)。
均值插补简单但缺乏吸引力,本质上给数据注入了与数据集中其他变量不相关的分数,这样在计算相关系数,协方差系数时便会受到削弱,即使数据是MCAR,这种方法也会扭曲结果参数估计。
2) 回归插补(Regression Imputation)
回归插补是用回归方程的预测值代替缺失值(Enders, 2010)。通过利用辅助变量Xk = (k = 1, 2, …, k)与目标变量Y的线性关系,建立回归模型,对目标变量的缺失值进行估计。回归插补操作起来比较简单,但是却容易忽略随机误差的影响,低估标准差和其他未知性质的测量值,同样会产生估计偏差(Enders, 2010)。
跟均值插补不同,回归插补带有一定的预测性,当我们用插补后的完整数据进行相关回归的时候,由于回归插补插入的是预测值,因此由其插补后数据计算的相关回归估计相较于均值插补会有明显的优势,就其效率而言,回归插补是一种更有效率的方法。但是回归插补也有局限性,最主要的一点,回归插补是基于明确是模型基础之上,这个模型可靠性很关键,如果该模型分布与总体分布相符,回归插补的效果可以保证,否则插补的效果会不理想。
3) 热平台插补(Hot-Deck Imputation)
热平台插补最早是美国人口统计学家为了处理公共缺失数据提出的一种方法(Scheuren, 2005)。热平台插补是从真实存在的未缺失数据中利用一定的规则和算法得出插补值(潘传快,2017)。相比与均值插补和回归插补,这种方法并不需要清晰的模型便能得出插补值。但是有研究者指出热平台插补不太适合估计相关性的统计量,并且可能产生对相关性和回归系数有很大偏差的估计(Brown, 1994; Schafer & Graham, 2002)。
热平台插补的优点是克服了均值插补和回归插补的虚拟感,也不会像回归插补会产生异常值。当然,热平台插补也有缺点,最主要的一点是其插补值来自观测值,这样插补后的数据中就会有很多的重复值,而且缺失值比例越大,插补值重复的概率就越高。
3.2.2. 多重插补(Multiple Imputation)
多重插补最早由Rubin (1987)提出,与上述单一插补方法相比较,多重插补方法充分地考虑了数据的不确定性。该方法是目前方法学家推荐的另一种最先进的缺失数据技术(Schafer & Graham, 2002)。多重插补的思想来源于贝叶斯推断,建立在贝叶斯理论的基础之上,用EM算法来实现对数据缺失值的处理(金勇进,邵军,2009)。多重插补的主要步骤可以分为三个步骤,综合起来即为:插补、分析、合并。第一步插补,这是最关键的一步,对每一个缺失数据插补m (m > 1)次,每次插补会产生一个完整的数据集,共m个数据集。第二步,对每一个完整数据集进行分析。第三步,将每次分析得到的结果进行综合,最后得出统计推断。其过程如图1所示。
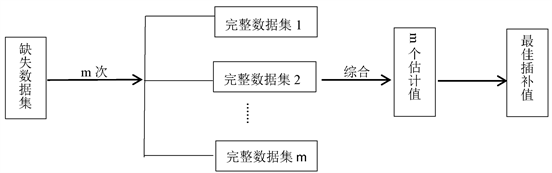
Figure 1. Principle of multiple imputation
图1. 多重插补原理
值得注意的是,多重插补要求数据缺失为MCAR机制,在MAR和NMAR机制下目前难以取得准确的估计值。其次在使用多重插补估计缺失值时需要考虑m的次数,有研究者认为当m取20时在多数情况下是比较合适(Graham, Olchowski, & Gilreath, 2007)。从理论上说m次数越大估计的结果就越精确,但是m次数越大带来的成本也就越高。
多重插补相比其他方法更有优势,首先,多重插补方法能够尽可能的利用其他辅助信息,给出多个替代值,保持了估计结果的不确定性(冯丽红,2014);其次,多重插补能够在接近真实情况下模拟缺失数据的分布情况,从而尽可能的保持变量之间的原始关系。
其他的插补法诸如k最近邻插补、决策树插补、支持向量机插补和神经网络插补等方法,由于文章篇幅有限,不做介绍,读者可以参考文献(廖祥超,2017)。
3.3. 基于模型的方法
基于模型的方法需要考虑缺失机制(MCAR、MAR和NMAR),在此基础上为缺失数据设定合适的模型,常用的方法有EM算法、极大似然估计、MCMC算法等。文章简单介绍EM算法在处理缺失值中的应用。
EM算法又叫期望值最大化法(Expectation Maximization),是由Dempster,Laird和Rubin所提出的一种专门用于求解参数极大似然估计的迭代算法(Dempster, Laird, & Rubin, 1977)。其最大的特点是通过数据扩张,将不完全数据的处理问题转化为对完全数据的处理问题(钱俊,舒宁,2004)。EM算法主要通过迭代实现,每一个迭代周期分别由两步组成:E步和M步。E步计算数学期望,即获得完全数据对似然函数关于缺失数据的期望;M步主要进行导数运算,即以E步求得的缺失数据的条件期望作为无回答的缺失值。最后经过多次E步和M步的迭代后,参数收敛后得到参数估计值。
图2是EM算法的具体步骤流程图。通过流程图可以清晰的看出算法的计算过程。
EM算法在计算缺失数据时,可以充分利用缺失数据的潜在信息,有效提高了数据处理的质量。但是,EM算法缺点在于,当缺失数据缺失量很大时,算法的收敛速度会减弱,且M步求得缺失数据的条件期望与真值偏差也会逐渐增大,结果求得的缺失值估计值便不理想。
4. 缺失数据处理方法比较评价
处理缺失值数据的方法有很多,但各有各的特点,每种处理方法都有其需要满足的要求。有研究者认为(庞新生,2010)大部分缺失值处理方法应满足如下假定:一是多元正态分布,二是所有变量独立同分布,三是数据随机缺失。在缺失数据处理之前,需要对上述条件做出判断。
一般而言,在使用缺失数据技术时,最需要考虑的是缺失数据处理方法所适用的数据缺失类型。如果缺失数据不是随机缺失的,数据分析可能将导致偏差;如果数据类型不是MCAR机制,将不适用与多重插补MI的方法;以模型为基础的方法如完全信息极大似然估计又需要数据类型满足MAR机制。因此,在对缺失数据处理前我们需要对样本分布是MCAR、MAR或是NMAR机制有一定的了解。
选择何种缺失数据的处理方法主要取决于数据的性质和质量、用途以及缺失数据的机制。据此,对文章上述各种缺失数据处理方法进行比较分析,主要内容见下表2。

Table 2. Missing data processing method comparison
表2. 缺失数据处理方法比较
根据上表,EM算法和多重插补适用范围广泛,处理缺失数据时,具有比其他方法更好的稳健性,其偏差也很小,不失为很好的选择,但是对于这些以模型为基础的方法操作起来存在困难,需要有一定的数学和计算机基础,适合具有处理缺失数据的专长和工具的研究者。
均值插补和回归插补虽然操作相比多重插补简单,但是其稳健性较差,常常会低估方差及抽样误差,在实际应用中并不是特别广泛。
最后,如果缺失数据非常少,数据缺失在5%之内,我们也可以采用列表删除的方法,而此时也不会引入大的误差,操作起来也比较容易简单。
5. 小结
综上所述,没有哪一种方法是既简单适用性又广误差又小的,每种方法都有各自的利弊,有着各自的适用的条件。因此,我们在选择方法时,应该注意了解调查数据的背景、特征等,尽可能地挖掘样本总体的各种辅助信息,此外对待缺失值处理方法也应该持一种科学谨慎的态度,毕竟方法在不断发展,现在的方法都不会一直是最优最好的方法,选择最合适的方法处理自己的数据才是最好的方法。