1. 引言
近年来,爆炸突发引起的灾害问题时有发生,在建筑结构上尤为常见。为了避免建筑物在突发爆炸事件中遭受重创,在结构设计时应当考虑爆炸冲击荷载,提出有效的抗爆设计方法 [1]。为此,有必要对炸药的爆炸特性进行研究。现阶段,对于爆炸冲击荷载在建筑物上的研究集中于小当量炸药,针对大当量炸药的研究较少。考虑到大当量炸药潜在的破坏威力,很有必要对其进行深入研究。目前对于爆炸冲击荷载的研究主要有实验和数值模拟两种方法。一般来说,TNT当量不小于1吨为大当量 [2]。大当量炸药下进行爆炸实验难度较大,所需设备以及实验条件复杂,实验数据难以获得。LS-DYNA软件可以模拟任何复杂结构计算问题,特别适合模拟碰撞、冲击、爆炸等各种非线性动力问题 [3]。本文利用LS-DYNA软件模拟大当量炸药在空气中自由爆炸现象,将数值模拟结果与多个经验公式进行对比,拟合成通用超压函数表达式,并对其合理修正。
2. 空气冲击波传播规律
炸药爆炸时,冲击波在空气中传播会形成双层球形的两个区域,外层为压缩区,内层为稀疏区 [4],如图1所示。压缩区的空气因受到压缩,压力远远超过正常大气压,也称为超压,超压是判断爆炸效应的重要参数之一。本文主要研究的就是超压峰值的变化。在空气冲击波向外传播的过程中,波阵面的压力迅速下降。原因如下:炸药爆炸过程中,产生的冲击波是球形的,随着传播距离的增大,波阵面的面积也在增加,这样就导致,即使在理想状态下,波阵面上单位面积分布的能量也会减小,再加上受空气环境因素的影响,会有不可逆的能量损失产生 [4],所以在波传播的过程中波阵面压力迅速减小,并且初始阶段衰减快,后期衰减速度变小,实验结果显示,衰减是按照指数规律衰减的,如图2所示。
3. 数值模拟和经验公式的对比
3.1. 建立爆炸模型和材料本构关系
本文采用ANSYS分别建立TNT当量为1,2,3,4,5 t时的空气爆炸模型,所有单元均采用solid164单元,炸药采用球体模型,尺寸如表1所示 [2],空气域采用立方体,尺寸为52 m × 52 m × 52 m,示意图如图3,网格尺寸都为0.4 m,采用kg-m-s单位制,为简化计算,考虑到对称性,可以采用部分建模的方式 [5],以1/8的模型进行计算,如图4,爆点设置在角点,在三个对称面设置对称约束,空气域所有边界面设置为无反射边界 [5]。
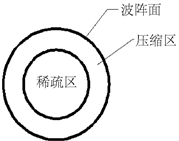
Figure 1. Spherical explosive shock wave propagation diagram
图1. 球形炸药冲击波传播图
空气采用NULL材料模型以及LINEAR_POLYNOMIAL状态方程 [6] [7],线性多项式状态方程为:
(1)
式中,P为爆轰压力;E为单位体积内能;V为相对体积。参数如表2所示 [2] :
炸药采用HIGH_EXPLOSIVE_BURN模型以及JWL状态方程 [8] [9] :
(2)
式中,P为爆轰压力,V为相对体积,E为单位体积内能,ω、A、B、R1、R2为材料常数。具体参数如表3 [2],其中E0为初始能量,V0为初始相对体积:

Table 2. Air material parameters and equation of state parameters
表2. 空气材料参数和状态方程参数

Table 3. Explosive material parameters and equation of state parameters
表3. 炸药材料参数和状态方程参数
图5为5 t炸药爆炸时,空气冲击波在不同时刻时波阵面的超压云图示例:
 (a) t = 0.005 s (b) t = 0.01 s (c) t = 0.015 s
(a) t = 0.005 s (b) t = 0.01 s (c) t = 0.015 s
Figure 5. Overpressure cloud example
图5. 超压云图示例
3.2. 经验公式
很多学者在理论指导的基础上,结合实验研究,对冲击波超压峰值提出了自己的见解,也总结出以下经验公式(单位:MPa):
1) M.A. Sadovskyi在1952年提出冲击波超压峰值计算公式 [10] :
(3)
2) Henrych公式在1979提出的计算超压峰值的表达式 [10] [11] :
(4)
3) Mills公式在1987年提出的计算TNT爆炸的超压峰值的方法 [11] [12] :
(5)
4) 我国国防工程设计规范(草案)中规定的空爆冲击波超压公式为 [4] :
(6)
5) 王儒策(1993)根据原子爆炸的经验装药提出在无限空气介质中爆炸的超压公式 [13] :
(7)
6) 人民防空地下室设计规范(GB50038-2005) [14] 中提到的公式为:
(8)
其中,Z为比例距离,
,R为测点与爆心的距离(m),W为炸药当量(kg)。
3.3. 结果误差对比
运用LS-DYNA软件计算数值模拟值,采用ALE算法,对经验公式值运用Matlab软件计算。考虑数值模拟的可行性,只针对1~5 t的TNT炸药进行模拟,研究
时各种工况下的超压峰值,结果如图6,图7所示。
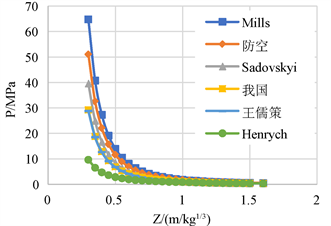
Figure 6. Six formula overpressure peak curve
图6. 六个公式超压峰值变化曲线图
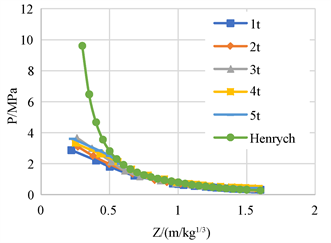
Figure 7. Overpressure peak curve of different equivalent TNT and Henrych formulas
图7. 不同当量TNT和Henrych公式超压峰值变化曲线图
由图6,图7可见:(1) Mills公式算值最大,Henrych公式算值最小,在
时,不同的经验公式之间及其与模拟值均相差较大。(2) 超压峰值随着炸药当量的增加有小幅度增加。(3) 无论是经验公式还是数值模拟结果,超压峰值变化均呈现先迅速下降再缓慢减小趋势,且在
时,他们之间结果基本吻合,说明计算模型和参数选取是合理的。
公式与数值模拟值之间出现差异有两个原因:(1) 经验公式是学者们通过实验研究得出来的,不同学者所处年代,实验设备以及环境条件不同,所得实验结果精确度不同,得出的经验公式有差异,尤其是在
时。(2) 数值模拟是基于理想环境条件建模分析的,而实际爆炸会受到周围环境的影响,比如反射波会对冲击波有加强作用,所以数值模拟值偏小。
3.4. 结果修正
综上可见:如果仅以数值模拟值预测实际爆炸状况,会低估爆炸的威力,存在安全风险。为了准确分析爆炸的威力,本文结合经验公式解,对数值模拟结果进行如下修正。
1) 根据最小二乘法,运用Matlab软件,取5种当量下的超压峰值平均值,拟合得到数值模拟通用超压函数表达式,如式(2.9):
(9)
由图8可得:拟合结果和各当量下的超压曲线吻合程度较大,拟合程度较高。
为了保证抗爆分析的可靠性,在数值模拟值基础上乘以一个修正系数,得到修正后的超压值
,如式(2.10):
(10)
依据数值模拟解与经验公式值可见,随着比例距离的增大,两者的差距越来越小,且其分布曲线与幂函数和指数函数相似,因此可用二者分别拟合修正系数。取以上六个经验公式的平均值
,将其作为参考值,使得
接近
,运用Matlab拟合得到以下两个公式:
幂函数
(11)
指数函数
(12)
对两个函数的拟合结果做误差分析如表4,可得:
的拟合误差控制在6.5%以内,但是
的拟合误差全部控制在2.5%以内,说明两者的拟合程度均较高,但指数函数更为恰当。
其中用到的符号:
为数值模拟解;
为经验公式平均值;
为修正超压值;
为修正系数;
为相对误差的绝对值。
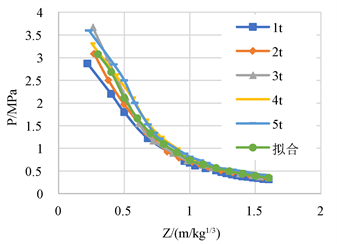
Figure 8. Comparison of simulation results and fitting results
图8. 模拟结果与拟合结果对比曲线
2) 为了验证式(2.9)和(2.12)的可靠性,建立6 t的炸药模型,拟合得到图9的对比曲线,结果可见:(a) 公式(2.9)可以很好的反映模拟结果,说明该函数具有普遍适用性;(b) 利用公式(2.12)修正后的结果与经验公式平均值吻合程度较高,说明了该修正系数函数是可靠的。
3) 为了验证式(2.9)和(2.12)的可靠性,建立6 t的炸药模型,拟合得到图9的对比曲线,结果可见:(a) 公式(2.9)可以很好的反映模拟结果,说明该函数具有普遍适用性;(b) 利用公式(2.12)修正后的结果与经验公式平均值吻合程度较高,说明了该修正系数函数是可靠的。
4) 综上所述,修正后的冲击波通用超压函数表达式可归纳如式(2.13)。为了在实际中应用方便,直接采用式(2.9)计算数值模拟值,避免繁琐的分析过程及对人员素质要求过高等问题;以式(2.13)计算修正后的超压值,避免采用不同经验公式计算引起的偏差。
(13)
4. 结论
通过上述对大当量TNT爆炸冲击波的超压分析,可得以下结论:
1) 不同的经验公式因为提出的背景、环境有差别,数据之间的差距较大,其中Mills公式值最大,Henrych公式值最小。
2) 运用LS-DYNA软件建立大当量TNT炸药在空气中爆炸的模型,得出数值模拟值比经验公式值小,如果仅以模拟解进行结构抗爆设计,存在低估爆炸威力的风险,但是可作为抗爆设计的下限参考值。
3) 通过不同工况的模拟值,拟合得到通用超压函数表达式(2.9),可以直接计算数值模拟结果,避免工程应用中繁琐的建模分析过程及对人员素质要求过高等问题;通过修正模拟值,归纳出通用修正超压函数表达式(2.13),该公式避免了不同经验公式计算引起的偏差,更好的指导结构针对大当量炸药的抗爆设计。
基金项目
国家自然科学科学基金资助项目(No. 11572235)与(No. 11702034)。