一种受径向载荷螺钉强度校核方法

Radial Load Screw Strength Check Method

摘要: 螺接是机械产品中使用最广泛的连接方式之一，对于受到复杂载荷特别是载荷量级较大的连接件，单个连接螺钉的断裂可能会导致其余螺钉依次断裂，最终损坏设备，甚至出现安全问题。本文针对受到径向载荷的螺接件进行受力分析，提出了该类型螺钉连接件的安全使用条件和校核公式，并针对某实例采用有限元法进行验证。结果表明：该计算方法可以得到螺钉危险位置的受力大小，可用于对受到复杂载荷的螺接件的螺钉进行校核。

Abstract: Screwing is one of the most widely used connection methods in mechanical products. For connectors that are subject to complex loads, especially those with large load levels, the breakage of a single connecting screw may cause the remaining screws to break in sequence, eventually damaging the equipment and even presenting safety issues. In this paper, the force analysis of screwed parts subjected to lateral load is carried out, and the safe use conditions and verification formulas of this type of screw connection are proposed. The finite element method is used to verify the example. The results show that the calculation method can obtain the force of the dangerous position of the screw, and can be used to check the screw of the screwed parts with complicated load.

1. 引言

工程上，螺栓若承受较大横向载荷，常常会选择铰制孔螺栓，其螺杆部分与孔之间过渡配合，依靠螺栓本身的抗剪作用防止被连接件的相对滑动。但是由于铰制孔螺栓具有强定位功能，配好后连接件位置不可调，对于夹具类等拆装反复性高的零件，或者在某些特殊的使用工况下，铰制孔螺栓并不适用，只能选择普通螺栓或螺钉，此时横向载荷主要靠预紧力带来的摩擦力承受。

机械设计过程中对螺钉连接强度进行校核是必不可少的环节。一般情况下，螺钉按照《机械设计手册》中的要求选型，使用通用或经验公式进行校核。螺钉正常的安装形式当如图1(a)所示，要求螺钉拧紧后，两零件不会发生相对滑动。

在实际情况下，由于打孔误差、装配误差，或者设备在使用中受到冲击或其它复杂载荷，可能会产生如图1(b)所示的螺接形式。此时，螺钉受到径向载荷作用，除了自身的预紧拉力，还可能受到剪力和弯矩。在这种情况下，螺钉不再是单向受拉。在多个螺钉共同作用时，由于“群体折减效应”，一旦发生破坏往往会在短时间内依次破坏。对于受力较大的承剪螺钉，必须考虑出现这种非正常情况下的安全性。

(a) (b)

Figure 1. Curve: screw connection mode: (a) Normal; (b) Abnormal

图1. 螺接形式：(a) 正常；(b) 非正常

2. 螺钉受力分析 [1]

非正常受力状况下的螺钉可以统一简化为如图2的计算模型。A端以下是被拧入螺孔的部分，B端代表螺钉头。AB段在被连接件的通孔内，长度为L。如此可视该螺钉为悬臂梁结构，在B端产生挠度ω和转角θ。螺钉头受到一个摩擦力F₁和力矩M，力矩由螺钉头和连接件表面的机械位置约束产生。螺钉杆存在初始的拧紧力P₀，同时螺钉杆上会受到零件滑移产生的剪力F₂。螺钉弯矩图见图2(c)。A点弯矩最大，同时还受到剪切和挤压应力，是上述状态中的薄弱点。

(a) (b) (c)

Figure 2. Curve: screw stress analysis

图2. 螺钉受力分析

螺钉头的挠度和转角由摩擦力F₁和力矩M引起：

$\{\begin{array}{l}\omega ={\omega }_F+{\omega }_M\\ \theta ={\theta }_F+{\theta }_M\end{array}$ (1)

其中：

$\begin{array}{l}{\omega }_F=-\frac{F_1{L}^2}{3EI},{\theta }_F=-\frac{F_1{L}^2}{2EI}\\ {\omega }_M=-\frac{M{L}^2}{2EI},{\theta }_M=-\frac{ML}{EI}\end{array}$

由图1，螺钉头的挠度和转角一般被机械结构约束，可以通过几何结构确定其最大值。F₁和M分别为：

$\{\begin{array}{l}{F}_1=\frac{6EI\left(2\omega -L\theta \right)}{\left(3L-4\right)L^2}\\ M=\frac{EI\left(-6\omega +4\theta \right)}{\left(3L-4\right)L}\end{array}$ (2)

其中，E是螺钉材料的弹性模量，I为螺钉截面的惯性矩， $I=\frac{\pi d_1^2}{64}$，d₁为螺钉的最小截面直径。

螺钉受到的弯矩见图2(c)，最大弯矩发生在A端，最大弯矩为：

$M_{\max }=M+F_{1}L=\frac{6EI\omega +EI\left(4-6L\right)\theta }{\left(3L-4\right)L}$ (3)

则螺钉受到的弯曲正应力为：

${\sigma }_M=\frac{M_{\max }}{\frac{\pi d_1^3}{32}}=\frac{E\left[6\omega +\left(4-6L\right)\theta \right]}{2d_{1}L\left(3L-4\right)}$ (4)

螺钉受到的预紧拉应力为：

${\sigma }_t=\frac{P_0}{A}=\frac{4P_0}{\pi d_1^2}$ (5)

其中P₀为螺钉预紧力，A为螺钉公称应力截面积。

则螺钉受到的轴向应力为：

${\sigma }_x={\sigma }_M+{\sigma }_t=\frac{E\left[6\omega +\left(4-6L\right)\theta \right]}{2d_{1}L\left(3L-4\right)}+\frac{4P_0}{\pi d_1^2}$ (6)

螺钉受到的剪切应力为：

$\tau =\frac{F_2}{A}=\frac{4F_2}{\pi d_1^2}$ (7)

螺钉杆受到的挤压应力：螺钉杆受到的挤压应力与挤压接触面积有关。理论上，接触面是一条无宽度的切线。但是由于材料一方面会产生弹性变形，另一方面表面粗糙度会导致“弱接触”情况下的接触刚度较小。而圣维南原理指出，荷载的具体分布只影响荷载作用区附近的应力分布。根据有限元计算中常用的边界设置方法，认为螺钉杆受剪后的接触面积如图3所示。螺杆径向的接触长度为1/3d₁，螺杆轴

向的接触长度为3倍螺距，即3P。接触面积 $A_p=\frac{1}{3}{d}_1\cdot 3P=d_{1}P$。

Figure 3. Contact area of the screw

图3. 螺钉的接触区域

则螺钉受到的挤压应力为：

${\sigma }_p=\frac{F_2}{A_p}=\frac{F_2}{d_{1}P}$ (8)

结合公式(6) (7) (8)，可以作出螺钉薄弱点的三向应力摩尔圆(图4)：

可以解得主应力为：

$\{\begin{array}{l}{\sigma }_1=\frac{{\sigma }_x+{\sigma }_p}{2}+\sqrt{{\left(\frac{{\sigma }_x-{\sigma }_p}{2}\right)}^2+{\tau }^2}\hfill \\ {\sigma }_2=0\hfill \\ {\sigma }_3=\frac{{\sigma }_x+{\sigma }_p}{2}-\sqrt{{\left(\frac{{\sigma }_x-{\sigma }_p}{2}\right)}^2+{\tau }^2}\hfill \end{array}$ (9)

螺钉薄弱点的最大正应力与最大切应力分别为：

$\{\begin{array}{l}{\sigma }_{\max }={\sigma }_1=\frac{{\sigma }_x+{\sigma }_p}{2}+\sqrt{{\left(\frac{{\sigma }_x-{\sigma }_p}{2}\right)}^2+{\tau }^2}\hfill \\ {\tau }_{\max }=\frac{{\sigma }_1-{\sigma }_3}{2}=\sqrt{{\left(\frac{{\sigma }_x-{\sigma }_p}{2}\right)}^2+{\tau }^2}\hfill \end{array}$ (10)

可以通过以上公式校核承受径向载荷螺钉的静强度。

Figure 4. Stress mole circle

图4. 应力摩尔圆

3. 实例计算

3.1. 离心场下静压轴承的螺钉连接方式

在某离心机上安装有四个全密封静压轴承，共同对某零件导向。这要求四个轴承运动轴线的平行度很高。而离心机由于体型较大，在不同温度和不同离心加速度情况下都会有比较明显的变形，从而破坏了轴承运动轴线的平行度。在工作中需要经常对轴承的位置进行微调，故轴承与离心机直接不能使用铰孔，只能用普通螺钉进行连接，从而留出调节余量，这就导致普通螺钉可能有受剪的风险。

图5所示为全密封静压轴承的外形图，底面有14个宽17 mm的马蹄槽，安装时，穿入14个M16的圆柱头内六角螺钉将轴承固定在基座上。底面的螺钉编号从1到14号。离心加速度的大小为100 g。

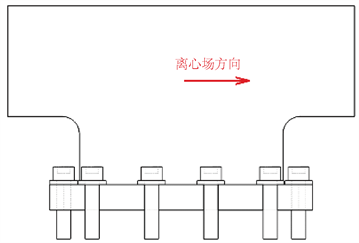
Figure 5. Curve: screw connection mode of fully sealed bearing

图5. 全密封轴承的螺接方式

在离心场下，轴承所受的离心力需要由底面摩擦力平衡。轴承被螺钉压紧在基座上，要求在离心场下轴承和基座不得有相对滑动。基于此，螺钉理论上仅受预紧力提供的拉力。

考虑到由于存在以下因素，给螺钉足够预紧力后，轴承仍可能发生滑动，导致螺钉受力：

1) 全密封轴承是精密的导向零件，对基座的平面度要求较高，精加工以后基座的粗糙度较小；

2) 安装调试轴承时，会在轴承底部垫铜箔，从而减小其摩擦系数。

因存在以上不确定因素，轴承的安装螺钉的选择要满足以下两个保证点：

1) 为满足轴承的正常使用条件，要求螺钉能提供足够预紧力，保证底面有足够摩擦力平衡轴承的离心力；

2) 为保证使用的安全性，要求一旦轴承发生侧滑，螺钉能承受由此引起的剪力，不会被剪断。

3.2. 螺钉预紧力计算

轴承被14个螺钉压紧在基座上，轴承的质量为45 kg，离心场下，产生Q = 45 kN的横向离心力。各螺栓预紧力P₀需要至少为：

$P_{0\min }=\frac{K_{n}Q}{zmf}=13.469\left(\text{kN}\right)$ (11)

其中：

Q为轴承受到的离心力，大小为45 kN；

K_n为可靠性系数，这里取1.1；

m为摩擦面数量，这里为1；

z为螺钉数量，这里为14；

f为摩擦系数，这里取为0.15 [2]。

为保证安全，选择12.9级的螺钉，该型螺钉的保证载荷为452 kN。初始拧紧力达到所需的5倍，设定为：

$P_0=67\left(\text{kN}\right)$ (12)

3.3. 螺钉受力计算

假设轴承由于某些特殊情况，摩擦系数f下降到0.02，产生的摩擦力不足以克服离心力，产生了滑移，对螺钉产生横向力。

每个螺钉头下的摩擦力大小变为：

$F_1=f\cdot P_0=1.29\left(\text{kN}\right)$ (13)

螺钉穿过的通孔直径为17 mm，螺钉上端直径为16 mm。考虑到打孔以及安装精度，各螺钉中心和孔中心会存在一个间距h，h_max = 0.5 mm；受到机械约束，螺钉帽与基座保持平行，其转角θ = 0。

根据公式(6)，可计算得出该离心场下螺钉的轴向应力，见公式(14)，位置在图1中的A点处：

${\sigma }_x=\frac{E\left[6\omega +\left(4-6L\right)\theta \right]}{2d_{1}L\left(3L-4\right)}+\frac{P_0}{A}=316\left(\text{MPa}\right)$ (14)

在连接交界面上，螺钉存在剪力。对于该全密封轴承，由于每个螺钉与孔的初始中心距h是不同的，故h最大的两个螺钉将最先与孔接触，接触点受到最大的集中力F₂。

$F_2=\frac{Q}{2}-12\times F_1=7\left(\text{kN}\right)$ (15)

根据公式(7)，螺钉受到的剪应力为：

$\tau =\frac{4F_2}{\pi d_1^2}=52.2\left(\text{MPa}\right)$ (16)

根据公式(8)，螺钉在接触面受到的挤压应力：

${\sigma }_p=\frac{F_2}{A_p}=\frac{F_2}{d_{1}P}=218\left(\text{MPa}\right)$ (17)

其中M16的螺距P = 2。

画出接触点的应力状态，作出其对应的摩尔圆(见图6)，根据公式(10)，得到螺钉的最大正应力与最大切应力为：

$\{\begin{array}{l}{\sigma }_{\max }={\sigma }_1=338.4\text{MPa}<\left[\sigma \right]\\ {\tau }_{\max }=\frac{{\sigma }_1-{\sigma }_3}{2}=71.4\text{MPa}<\frac{\left[\sigma \right]}{2}\end{array}$

说明螺钉满足受力条件，即便轴承发生滑动，系统仍是安全的。

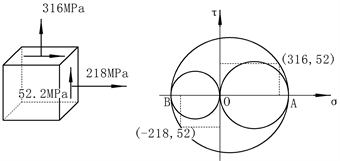
Figure 6. Curve: screw stress and Moore circle of maximum stress point

图6. 螺钉受力简图及最大受力点的摩尔圆

3.4. 有限元法验证

在一些复杂装配体的有限元仿真中，对于螺接关系的处理有时会直接用节点之间的耦合或者约束来代替，这样做通常不能够反映螺钉本身的受力特性。文献 [3] [4] 对螺钉的有限元建模及分析进行了研究，通过对螺钉及被连接件进行接触的定义、对螺钉施加预紧力等方式，可以得到较为准确的仿真结果。本文采用相似的方法，对静压轴承的螺钉进行有限元分析。模型的网格划分如图7所示，对螺钉、垫片以及底座连接面的网格划分较细，对非关注区域的网格划分较粗。

Figure 7. Curve: model meshing

图7. 模型网格划分

网格采用C3D8R (8节点六面体单元)，共89,358个单元，该单元克服了在线性完全积分单元中的剪切与自锁问题，在单元扭曲比较小的情况下，得到的位移和应力结果更精确；同时在弯曲问题中，厚度方向只需要很少的单元，就可以得到与二次单元相当的结果，而计算成本可以明显降低。

3.4.1. 边界条件与载荷设置

共设置两个分析步：第一个分析步仅施加40,000 N的螺钉预紧力，第二个分析步给轴承施加100 g的离心加速度。

螺钉头与垫片、垫片与轴承底座表面设置接触边界，摩擦系数与上文一样设置为0.02。约束轴承底座在垂直方向的自由度，约束螺钉下部拧入基座部分的水平自由度，如图8所示。

Figure 8. Curve: boundary conditions

图8. 边界条件

垫片选用型号：钢结构用高强度垫圈 [5]。厚3 mm，其中 ${\sigma }_b\ge 700\text{Mpa}$。

3.4.2. 仿真分析结果

仿真分析结果见图9：

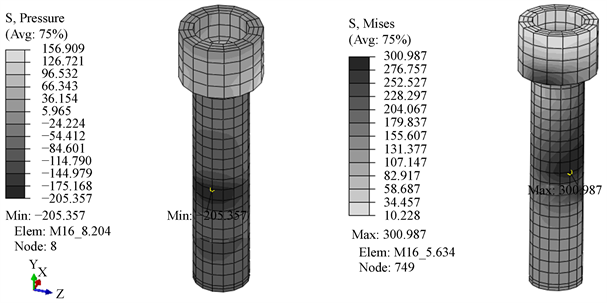
Figure 9. Surface pressure (left) and stress cloud map (right)

图9. 螺钉受到的表面压强(左)与螺钉应力云图(右)

将仿真分析计算结果与公式法计算结果进行比较，如表1所示：

Table 1. Comparison of formula calculation results and finite element calculation results

表1. 公式法和有限元法计算结果对比

4. 结束语

1) 公式法和有限元法的计算结果差别很小，其中公式法得到的结果比有限元法的结果略大，在实际应用中则更加安全，证明了公式法的正确性。螺钉的最大应力点出现在连接交界面位置。

2) 螺钉受到横向载荷，最好使用铰制孔螺栓；但如果只能使用普通螺钉时，须考虑螺钉在非正常工作状态下不被破坏。这种情况可以采用文中给出的计算方法进行校核，以便设计人员进行选型。

3) 如果螺钉还受到交变载荷的作用下，需要额外进行疲劳校核。