KinectV2传感器实时动态手势识别算法

KinectV2 Sensor Real-Time Dynamic Gesture Recognition Algorithm

摘要: 为解决动态手势动作识别算法提取的特征泛化程度低，识别实时性差和识别率不高的问题，本文提出了一种基于KinectV2传感器的模板匹配手势识别方法。该方法利用Kinect Studio和Visual Gesture Builder建立手势动作数据库，提取人体关键骨骼间的夹角作为随时间变化的一维特征向量，借助动态规划思想，在动态时间规整(DTW)算法的基础上提出了加权DTW手势动作识别算法。通过对DTW算法的改进，使其规整路径更快的收敛，提高了手势动作识别的实时性和准确性，并在Unity 3D虚拟仿真实验平台中进行了实时性和有效性的验证实验，同时实现了简单的人机交互。

Abstract: In order to solve the problems of low generalization of features extracted by the dynamic gesture action recognition algorithm, poor real-time recognition and low recognition rate, this paper proposes a template matching gesture recognition method based on KinectV2 sensor. This method uses Kinect Studio and Visual Gesture Builder to build a gesture action database, extracts the angle between key bones of the human body as a one-dimensional feature vector that changes with time, and proposes Weighted DTW gesture motion recognition algorithm based on the dynamic time warping (DTW) algorithm with the help of dynamic planning ideas. Through the improvement of the DTW algorithm, the regular path converges faster, the real-time and accuracy of gesture motion recognition is improved, and the real-time and validity verification experiments are carried out in the Unity 3D virtual simulation experiment platform for simple human-computer interaction.

1. 引言

现代石油工业发展迅猛，规模不断增大，人们对其工艺水平要求越来越严格。但在实际生产中，随着石油产业规模的加大，往往会带来爆炸、有毒物质泄露等安全因素，因此，可引入手势别技术，使用手势对单体化工设备进行放缩，旋转等操作，使一线生产工人对设备外观等有更直观的了解，此外，还可以在虚拟现实平台进行事故演习时控制灭火器，阀门旋转等来模拟事故现场应急方案。从而为石化装置生产一线人员提供一个真实感官效果、状态信息明确、操控方便的全新工作环境 [1]。

手势识别技术在半个世纪前就开始有所体现，在2010年11月，随着微软公司推出Kinect体感交互设备，手势交互技术迅速被众多研究人员视为研究热点，尤其是其在骨骼追踪，预测及人体定位有着非常好的准确度，可以说是人机交互的一个革命性产品，随着Kinect for Windows SDK的推出，研究人员可以更加方便的获取用户的骨骼位置信息等，可以更加理解使用者的手势意义，从而可以帮助用户完成更好的人机交互体验。

通过研究发现，语音识别算法和手势识别算法基本形同，主要有矢量量化，轨迹追踪和模板匹配三种方法 [2]，因为矢量化的识别算法识别效率比较低，现在已经基本不再研究，所以近年来的手势识别算法主要是以隐马尔科夫模型(HMM)为代表的轨迹追踪算法和以动态时间规整模型(DTW)为代表的模板匹配算法。郭晓利等人 [3] 提出了一种改进的HMM模型算法，该算法与模糊神经网络相结合，比原HMM模型要稳定，但是还没有应用到实际中，还有待在实际环境中进一步检测。Saha S等人 [4] 提出了一种特征描述子用来描叙单个时间序列的扭曲信息，结合HMM模型来进行手势识别，该方法对12种不同的手势进行了测试，虽然准确度较高，但由于该方法模型较为复杂，所以实时性较差。李凯等人 [5] 提出了一种改进的动态时间规整算法，该方法将获取到的Kinect的骨骼点坐标及手型数据结合，构造了矢量特征来描述手的运动轨迹，实现了手势的快速匹配，但未考虑到每个人因骨骼坐标位置不同而对识别结果带来的影响；Ruan X等人 [6] 提出了一种通过失真度阈值和路径约束来改进DTW的算法，该方法通过选取8个点作为手部特征建立手势的数学模型，实验结果表明，该方法无论是在识别率还是鲁棒性方便，都取得了很好的实验效果。综上所述，HMM和DTW算法在手势明显的情况下，分类效果差别不大，通常情况下，HMM算法的识别率是要稍高于DTW算法，但是HMM方法模型复杂，计算量较大，因此实时性不如DTW算法，很难在实际生活中应用。

本文针对提取骨骼坐标位置特征时，因个人骨骼坐标位置不同造成的识别效率低，实时性差的缺陷，提出了一种基于KinectV2传感器骨骼数据的改进DTW模板匹配手势识别算法。该算法通过提取人体关键骨骼间的夹角特征，改善了因每个人骨骼位置不同造成的对手势动作特征描述不准确的缺点；通过对DTW算法进行改进，提高了计算速率，使动态规整路径更快的收敛。本文的算法不受骨骼坐标位置差异影响，能够使路径更快的收敛，既满手势识别的准确性，又满足实时性。

2. Kinect骨骼跟踪技术

Kinect SDK 2.0中提供了人体的各个骨骼关节的空间坐标位置分布信息及相对位置的变化，骨骼节点的数据类型以骨骼帧的形式表示，每一帧都是由25个骨骼节点组成的JointType类型的集合 [7]，人体各部位节点位置标注图和编号如图1所示。根据KinectV2追踪骨骼数据的状态在Kinect SDK 2.0中定义了三种骨骼节点跟踪情况：能够进行跟踪(Tracked)、不能够进行跟踪(Not Tracked)、通过运动状态进行推断跟踪(Infered) [8]。

Figure 1. Contrast map of human skeleton node

图1. 人体骨架节点对照图

3. 建立手势样本库

本文在建立手势样本库过程中主要分为录取手势，制作手势正负样本和通过程序代码调用手势样本库三个步骤，具体步骤的工具和如图2所示：

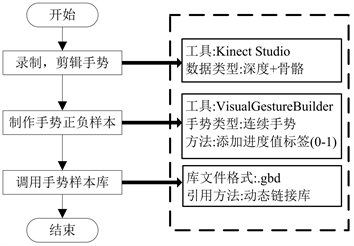
Figure 2. Gesture sample library building flowchart

图2. 手势样本库建立流程图

4. 手势运动特征提取

如何提取低计算量，低复杂度的特征并且找到统一的动作特征来对人体动作进行识别，是手势识别过程中的关键问题。以往的研究者们在进行骨骼动作的识别的时候，主要提取位置特征，角度特征或者速度特征来描述手势的运动 [9]，然而对于不同身高，不同体型的人做同一动作或者同一个人做不同动作的过程中，由于每个人的骨骼关节位置信息有一定的差异，运动速度也不尽相同 [10]，均不能统一而准确的描述手势的运动，但是即使每个人的骨骼坐标位置和运动速度不同，在运动过程中，关节间的夹角特征并没有发生明显变化，基于这种现状，本文中提出了将手势运动过程中的骨骼间的向量夹角作为手势特征描述，并结合动态时间规整(DTW)算法进行模板匹配，夹角特征提取过程如下。

4.1. 人体骨骼节点坐标获取

如图3所示，以求取右手手腕，右肩和颈下脊椎之间的夹角为例，其中，WR代表右手手腕关节点，SR代表右肩关节点，SS代表颈下脊椎关节点，要想求它们之间的空间向量的夹角，则需要求其关节点的空间坐标位置。

Figure 3. Diagram of joint angle

图3. 关节夹角示意图

虽然KinectV2能够得到人体各骨骼节点图像，但是却不能够直接获取其各个节点的空间坐标位置，所以我们需要通过编程的方式来采集需要的关节点坐标，如果将KinectV2捕捉的25个关节点全部用来做人体运动的特征分析，则会增加本系统的计算量和复杂度，从而影响系统的实时性，考虑到文中所识别的手势只用到了人体上半身的8个关键骨骼点，所以只对上半身的8个骨骼节点坐标进行提取，由于篇幅原因，表1中只列出了其中一组关键骨骼节点的空间位置坐标。

Table 1. Coordinate positions of key skeletal nodes

表1. 各关键骨骼节点坐标位置

4.2. 夹角特征提取

如图3，假设WR关节点的坐标为，SR关节点的坐标为 $\left(x_2,y_2,z_2\right)$，SS的关节点坐标为 $\left(x_3,y_3,z_3\right)$，则向量 $a=\left(x_2-x_1,y_2-y_1,z_2-z_1\right)$，向量 $b=\left(x_3-x_2,y_3-y_2,z_3-z_2\right)$，设 $\langle a,b\rangle$ 之间夹角为a，则有：

$\cos \alpha =\frac{a\cdot b}{\left|a\right|\left|b\right|}$ (1)

$a\cdot b=\left(x_2-x_1\right)\left(x_3-x_2\right)+\left(y_2-y_1\right)\left(y_3-y_2\right)+\left(z_2-z_1\right)\left(z_3-z_2\right)$ (2)

$\left|a\right|=\sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2+{\left(z_2-z_1\right)}^2}$ (3)

$\left|b\right|=\sqrt{{\left(x_3-x_2\right)}^2+{\left(y_3-y_2\right)}^2+{\left(z_3-z_2\right)}^2}$ (4)

将上述中的式(2)，(3)，(4)代入式(1) 即可求出三个关键骨骼关节点两两连成的向量的夹角。如图4所示，使用上述方法分别测出了某一帧右手手腕，右肘，右肩之间的夹角和颈下脊椎，右肩，右手肘之间的夹角。

Figure 4. The angle between skeletons: (a) Right wrist, right elbow and right shoulder; (b) Lower cervical spine, right shoulder and right elbow

图4. 不同骨骼间夹角角度：(a)右手手腕，右手肘和右肩的夹角；(b)颈下脊椎，右肩，右手肘的夹角

5. DTW算法原理介绍及实验分析

动态时间规整(DTW)算法是一种模板匹配方法，最开始用于处理语音序列长短不一的模式匹配问题，由于手势序列也是长短不一的，因此DTW算法也成为手势识别中常用的一种方法。

动态时间规整算法实际上是一个典型的优化问题，即利用距离函数计算出的距离值表示两个模板或者动作序列之间的相似度。如果两模板长度相等，则可以直接计算出这两个模板序列的距离来进行匹配识别；如果长度不相等，则需要将它们在时间轴上对齐，这时引入一个矩阵A，用该矩阵里面的每一个元素 $\left(i,j\right)$ 表示两模板元素之间的距离 $d\left(L_i,C_j\right)$，这个距离就代表模板L和模板C的相似度。

本次实验中使用的欧氏距离函数计算方法，因为它可以计算任何维度空间内的两个点之间的距离，如在二维平面空间里，两点之间的距离公式可以表示为：

$d=\sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2}$ (5)

在三维立体空间里，任意两点之间的距离公式可以表示为：

$d=\sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2+{\left(z_1-z_2\right)}^2}$ (6)

基于欧式距离的最短距离计算共有三个约束条件 [10]：

1) 边界性：规划的路径必须是从引入的矩阵的左下角开始，以右上角结束。

2) 连续性：路径上的点与相邻的点必须对齐，这样做的目的是为了保证计算到L和C中的每一个点。

3) 单调性：路径上的点相对时间轴必须呈递增状态。

按照上述约束条件可以推出，对于A中的每一个元素而言，有且只有三个元素与之相连，元素的节点分布图如图5所示：

Figure 5. Element node distribution map

图5. 元素节点分布图

这里我们定义一个累积距离s(i, j)，对L和C这两个模板序列从起点(1, 1)点进行计算，累计之前所有的点计算的距离，即累计点l_i与点g_j之间的距离，

再加上其周围与点(i, j)距离最小的那个点之间的距离，如式(7)所示。当匹配到达终点(m, n)的时候，距离值s(i, j)则代表这两个时间序列的相似度。

$s\left(i,j\right)=d\left(L_i,C_j\right)+\min \left\{\begin{array}{l}s\left(i-1,j\right)\\ s\left(i,j-1\right)\\ s\left(i-1,j-1\right)\end{array}\right\}$ (7)

累计距离和相似度成反比，累计距离越小，两个动作模板之间的相似度越高，累计距离越大，两个动作模板之间的相似度越低 [11]。在这里，为了更好的理解DTW算法，我们举例进行详细说明，如图9所示，分别为长度为5的标准模板{A, B, C, D, E}和长度为4的测试模板为{F, G, H, I}，模板中各元素距离已经给出，为了找出这两条模板最短的匹配路径，现在假设该模板满足下面的前提：点 $\left(i-\text{1},j\right)$ 、 $\left(i-\text{1},j-\text{1}\right)$ 、 $\left(i,j-1\right)$ 作为起点，点 $\left(i,j\right)$ 作为与之相连的点，如果从 $\left(i-\text{1},j\right)$ 到 $\left(i,j\right)$ 或者从 $\left(i,j-1\right)$ 到 $\left(i,j\right)$，则距离为 $d\left(i,j\right)$，如果是从 $\left(i-\text{1},j-\text{1}\right)$ 到 $\left(i,j\right)$，距离为 $\text{2}d\left(i,j\right)$，式(8)表示其前提条件为：

$g\left(i,j\right)=\min \left\{\begin{array}{l}g\left(i-1,j\right)+d\left(i,j\right)\\ g\left(i-1,j-1\right)+2d\left(i,j\right)\\ g\left(i,j-1\right)+d\left(i,j\right)\end{array}\right\}$ (8)

我们假设 $g\left(0,0\right)=0$，则 $g\left(1,1\right)=g\left(0,0\right)+2d\left(1,1\right)=4$ ；而 $g\left(\text{2},\text{2}\right)$ 的计算分三条路径比较：如果将 $g\left(1,\text{2}\right)$ 作为起点 $g\left(2,2\right)=g\left(1,2\right)+d\left(2,2\right)=9+3=12$ ；如果将 $g\left(1,\text{1}\right)$ 作为起点， $g\left(2,2\right)=g\left(1,1\right)+2d\left(2,2\right)=4+6=10$ ；如果将 $g\left(2,\text{1}\right)$ 作为起点， $g\left(2,2\right)=g\left(2,1\right)+d\left(2,2\right)=8+3=11$。

根据上述距离值计算，取最小值， $g\left(2,2\right)=10$ ；以此类推，矩阵A中两个模板的最优匹配路径经过的格点为(1, 1), (2, 1), (2, 2), (2, 3), (3, 4), (4, 4), (4, 5)，如图6红线所示：

Figure 6. Optimal matching path

图6. 最优匹配路径

本次实验中采用的动态时间规整算法对手势进行识别的具体设计步骤如图7所示：

Figure 7. DTW algorithm flow

图7. DTW算法流程

这里以左滑手势为例，利用Visual Studio和Matlab混合编程环境进行分析，这个手势主要是基于颈下脊椎，左肩，右肘这三个关键骨骼节点间的夹角进行判断，将这三个关键骨骼点每一帧形成的夹角作为一组关节角度向量来进行左滑动作的描述，测试者在做左滑手势时的关节角度变化的曲线如图8所示：

Figure 8. Angle change curve of left sliding gesture joint of tester

图8. 测试者左滑手势关节角度变化曲线

从图8中可以看出，关节间夹角的角度变化是一条随时间的变化而不断变化的曲线，可以反映出左滑这个动作的手势特征，角度的变化可以用关于时间的一维向量表示。

由于每个人的身高，体型，运动速度的不同导致手势完成的时间和每一帧的角度变化范围也不相同，虽然角度变化曲线的起伏程度不完全相同，但是从整体上来看，曲线的基本形状确是一样的，在进行模板匹配时，DTW会将长短不一的模板序列在时间轴上进行扭曲对齐，两模板序列关于时间轴的扭曲对齐实验仿真结果如图9所示。

Figure 9. Time distortion alignment experiment in template matching

图9. 模板匹配过程中时间扭曲对齐实验

经过上述实验步骤后，就可以寻找两模板之间的最优匹配路径，这里还是以左滑手势为例，samples为时间序列为128帧的标准模板，test为时间序列为100帧的测试模板，因为参考模板和测试模板的长度不一致，所以进行了时间序列的扭曲，将长短不一的时间序列特征进行了对齐，如图9所示。将时间序列进行对齐后，计算两模板的最优匹配路径和欧式距离，进而计算累计距离，当累计距离越小时，则表明两模板的相似度越高，左滑手势的测试模板和标准模板的最优路径匹配结果如图10所示：

Figure 10. Optimal matching path result of left-slip gesture

图10. 左滑手势最优匹配路径结果

6. DTW算法改进

由图11所示，左滑手势两模板的规整路径是弯曲上升的一条折线，而理想状态下的规整路径应该是一条接近对角线，接近直线的路径。变为图11所示路径的原因是随着样本数量和计算量的增加，识别精度随之降低，导致其动态时间规整路径无法趋向于对角线，为提高手势动作的识别精度和实时性，我们对DTW算法做出如下改进：

规整路径的累计值如式(7)可以计算得出，主要用来衡量和计算两条时间序列的相似度，为了使规整路径更加趋向于对角线，文中进行了如下改进：

$s\left(i,j\right)=d\left(L_i,C_j\right)+\min \left\{\begin{array}{l}{\sigma }_{1}s\left(i-1,j\right)\\ {\sigma }_{2}s\left(i,j-1\right)\\ {\sigma }_{3}s\left(i-1,j-1\right)\end{array}\right\}$ (9)

其中， ${\sigma }_1$， ${\sigma }_2$， ${\sigma }_3$ 为改进DTW算法的优化系数，根据图7所示，要想使路径趋近与对角线，则应使 $s\left(i-1,j-1\right)$ 大于 $s\left(i-1,j\right)$ 和 $s\left(i,j-1\right)$，理想状态下，假设当 $s\left(i-1,j\right)$ 和 $s\left(i,j-1\right)$ 均为1时，则 $s\left(i-1,j-1\right)$ 应为 $\sqrt{2}$，因此若想使路径尽可能的趋向对角线的概率变大，应使 $s\left(i-1,j\right)$ 和 $s\left(i,j-1\right)$ 中的最大值大于 $\sqrt{2}s\left(i-1,j-1\right)$，所以在无法比较 $s\left(i-1,j\right)$ 和 $s\left(i,j-1\right)$ 的前提下，分别对 ${\sigma }_1$ 和 ${\sigma }_2$ 取大于 $\sqrt{2}$ 小数倍，所以本文中的优化系数 ${\sigma }_1$， ${\sigma }_2$， ${\sigma }_3$ 的值分别为1.5，1.5，1。为验证改进DTW算法的有效性和准确性，文中针对左滑手势时间序列的规整路径进行了DTW算法改进前后的实验对比，如图11所示：

Figure 11. Comparisons of regular path before and after improvement of DTW left-sliding gesture

图11. 左滑手势DTW算法改进前后规整路径对比结果

由图11所示，改进后的DTW算法比改进前的DTW算法更接近于对角线，相对于改进前的DTW算法，改进后的DTW算法计算量较少，用来存储数据的空间需要的也更少，能够更快的收敛，有效的提升了识别算法的效率，提高了手势识别的准确性和实时性。

7. Unity3D虚拟现实平台实时交互实验验证及结果分析

7.1. Unity3D虚拟显示平台实时交互实验

实验中共定义了上滑，下滑，左滑，右滑，左转，右转，放大，缩小这8种手势，为了验证本文中手势的实时性和有效性，将定义和训练好的手势动作向虚拟现实中的单体设备发出控制命令，使单体设备响应动作，从而完成与虚拟现实场景的实时交互，手势控制指令与动作响应对照表如表2所示。

Table 2. Control instruction and action response table

表2. 控制指令与动作响应表

虚拟场景中的单体设备对手势控制指令的响应效果如图12所示：

(a) (b) (c) (d) (e) (f) (g) (h)

Figure 12. Comparisons of regular path before and after improvement of DTW left-sliding gesture. (a) Swipe up gesture response; (b) Swipe down gesture response; (c) Swipe left gesture response; (d) Swipe right gesture response; (e) Turn left gesture response; (f) Turn right gesture response; (g) Zoom out gesture response; (h) Zoom in gesture response

图12. 左滑手势DTW算法改进前后规整路径对比结果。(a) 上滑手势响应；(b) 下滑手势响应；(c) 左滑手势响应；(d) 右滑手势响应；(e) 左转手势响应；(f) 右转手势响应；(g) 缩小手势响应；(h) 放大手势响应

7.2. 实验结果分析

这种通过Kinect自己建立数据库的方法，能够训练多种复杂的连续手势，能满足用户的各种手势需求，使用户进行人机交互时更加方便，自然，本文通过提取关键骨骼点间的角度序列作为特征，利用提出的加权DTW算法进行分类和识别，提高了识别率的准确性和实时性，各个手势的识别率如表3所示，与黄东方等人 [12]，薛俊杰等人 [13] 和阮晓钢等人 [14] 的研究算法对比结果如图13所示。

Table 3. Gesture recognition rate

表3. 各手势识别率

Figure 13. Comparison of recognition rate with other literature algorithms

图13. 与其他文献算法识别率对比

为验证文中改进DTW算法的实时性，文中选择对其中6种手势分别采用了HMM算法，矢量特征+DTW算法和多项式时间算法+DTW算法进行手势处理时间的对比，每种手势测试50次，然后计算每种手势每次的平均处理时间，单位为ms/次，对比结果如表4所示：

Table 4. Real-time comparison of algorithms

表4. 各算法实时性对比

8. 结论

由表3和图13可知，本文中对定义的手势的平均识别率为92.5%，本文算法的平均识别率与黄东方等人的算法识别率相比高4.5个百分点，高于贺霄琛等人的算法2.7个百分点，高于阮晓钢等的算法2.2个百分点，由图13可知，本文中的算法识别率高于其他参考文献算法的识别率，由表4可以看出，本文中的改进DTW算法对每个手势的处理时间远远少于其他各算法，有较好的实时性。通过以上各项试验数据和交互实验结果可以看出本文中的研究方法能够取得良好的实验效果，实验方案有效可行。

基金项目

天津职业大学科学研究基金项目(20121101)；国家自然科学基金(F2012203111)资助项目；河北省高等学校科学技术研究青年基金项目(2011139)。