依赖随机选择与偶轮的广义Turán数

Dependent Random Choice and Generalized Turán Numbers of Even Wheels

摘要: 令G表示n个顶点的图，K₃表示图G中的三角形。W_2L^s 表示中心有s个顶点，外围是一个2l长的偶圈，且偶圈上的2l条边都与中心的s个点相连的一个图；P_L^s 表示中心有s个顶点，外围是一条l长的路，且路上的l条边都与中心的s个点相连的一个图。在本文中，我们主要利用依赖随机选择技术证明了下述广义Turán数：

Abstract: 1)。 2)。 Let G be a graph on n vertices, and K₃ be a triangle in graph G. We denoted by W_2L^s a graph with s vertices in the center, a 2l long even circle in the periphery, and 2l edges on the even circle are connected with s vertices in the center; and P_L^s represents a graph in which the center has s ver-tices, the periphery is an l-long road, and ledges of the road are connected with s vertices of the center. In this paper, we mainly proved that the following generalized Turán number by using the technique of dependent random choice: 1) . 2).

1. 引言

令 $\mathcal{F}$ 表示一些图组成的集族，如果对于任意的 $F\in \mathcal{F}$，图G都不包含F作为子图，那么称图G是不包含族 $\mathcal{F}$ 的。Turán数 $ex\left(n,\mathcal{F}\right)$ 定义为在n个顶点且不包含 $\mathcal{F}$ 的图G的最大边数。如果集族 $\mathcal{F}$ 仅包含一个简单图F，我们可以用 $ex\left(n,F\right)$ 代替 $ex\left(n,\left\{F\right\}\right)$。令 $P_l$ 表示l长的路，在1959年，Erdös和Gallai [1] 计算了图G中有关 $P_l$ 的Turán数。

定理1.1：(Erdős, Gallai [1] )令G是一个n个顶点的图， $P_l$ 表示l长的路，那么 $ex\left(n,P_l\right)\le \frac{1}{2}\left(l-1\right)n$。

随后在1965年，Erdős [2] 又计算了有关偶圈的Turán数，Bondy和Simonovits [3] 对此进行了证明。

定理1.2：(Erdös [2] )令G是一个n个顶点的图， $C_{2l}$ 表示2l长的偶圈，且 $l\ge 2$，那么存在正整数C，使得 $ex\left(n,C_{2l}\right)\le C{n}^{1+\frac{1}{l}}$。

现在，关于Turán数已经有大量的研究，详见综述文献 [4] [5]。

令T表示一个简单图，广义Turán数 $ex\left(n,T,\mathcal{F}\right)$ 定义为n个顶点的不包含 $\mathcal{F}$ 的图G中T复制的最大个数。如果 $T=K_2$，那么广义Turán数 $ex\left(n,T,\mathcal{F}\right)$ 就是经典的Turán数 $ex\left(n,\mathcal{F}\right)$。同样的，对于一个简单图F，我们通常用 $ex\left(n,T,F\right)$ 代替 $ex\left(n,T,\left\{F\right\}\right)$。最近，广义Turán数问题的研究也受到了广泛的关注，详见文献 [6] [7] [8] [9]。

$K_t$ 表示t个顶点的完全图。在1962年，Erdős [10] 首先计算了完全图的广义Turán数：

$ex\left(n,K_t,K_r\right)=\underset{0\le i_1\le \cdots \le i_t\le k-2}{{\displaystyle \sum }}\underset{r=1}{\overset{t}{{\displaystyle \prod }}}\frac{n+i_r}{k-1}.$

与Erdös-Stone定理相类似，Alon-Shikhelman [6] 证明了：对任意的图H，如果图H的色数 $\chi \left(H\right)=k$，并且当 $k>t$ 时，那么 $ex\left(n,K_t,H\right)=\left(1+o\left(1\right)\right)\left(\begin{array}{c}k-1\\ t\end{array}\right){\left(\frac{n}{k-1}\right)}^t$ ；当 $k\le t$ 时，那么 $ex\left(n,K_t,H\right)=o\left(n^t\right)$。Bollobás和Győri [7] 证明了在n个顶点的图G中不包含 $C_5$ 时， $K_3$ 的个数为： $\left(1+o\left(1\right)\right)\frac{1}{3\sqrt{3}}{n}^{\frac{2}{3}}\le ex\left(n,K_3,C_5\right)\le \left(1+o\left(1\right)\right)\frac{5}{4}{n}^{\frac{2}{3}}$。Győri和Li [11] 证明了在n个顶点的图G中不包含 $C_{2l+1}$ 时， $K_3$ 的个数为： $\left(\begin{array}{c}k\\ 2\end{array}\right)e{x}_{bip}\left(\frac{2n}{k+1},C_4,C_6,\cdots ,C_{2k}\right)\le ex\left(n,K_3,C_{2l+1}\right)\le \frac{\left(2k-1\right)\left(16k-2\right)}{3}ex\left(n,C_{2k}\right)$。Alon-Shikhelman [6] 又对上述两个结果的上界进行了改进，得到：1) $ex\left(n,K_3,C_5\right)\le \left(1+o\left(1\right)\right)\frac{\sqrt{3}}{2}{n}^{\frac{2}{3}}$ ； 2) $ex\left(n,K_3,C_{2l+1}\right)\le \frac{16\left(k-1\right)}{3}ex\left(\frac{n}{2},C_{2k}\right)$。

依赖随机选择是图论中一种简单而且有用的方法。早期，这种技术是被Rödl，Gowers，Kostochka以及Sudakovd等人 [12] [13] [14] 证明而且应用推广的。这个基本方法，也是一个著名的概率办法，详见文献 [15]。现在，依赖随机选择技术已经被应用到更多方面，比如：极值图论、拉姆齐理论、可加组合数学、组合几何等。

引理1.3：(依赖随机选择引理)令a，m，r，n都是正整数，d是一个正实数。G表示n个顶点的图，其平均密度为d。如果存在正实数t，使得

$\frac{d^t}{n^{t-1}}-\left(\begin{array}{c}n\\ r\end{array}\right){\left(\frac{m}{n}\right)}^t\ge a,$

那么图G中存在一个大小至少是a的子集U，使得U中任意r个顶点在图G中至少有m个公共邻点。

并且利用依赖随机选择技术，可以计算出有关二部图H的Turán数。

定理1.4：(Alon et al. [16] )令s是一个正整数， $H=\left(A,B\right)$ 是一个二部图，且B中顶点的度 $d_B\le s$。那么存在一个常数 $c=c\left(H\right)$，使得

$ex\left(n,H\right)\le c{n}^{2-\frac{1}{s}}.$

在n个顶点的图G中，令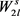表示中心有s个顶点，外围是一个2l长的偶圈，且偶圈上的2l条边都与中心的s个顶点相连接的一个图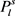；表示中心有s个顶点，外围是一条l长的路，且路上的l条边都与中心的s个顶点相连接的一个图。本文中，我们主要利用依赖随机选择技术得到下述两个结果：

定理1.5：假设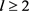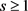，，且C和c是两个正数。令G是n个顶点的图，且边数为e，那么

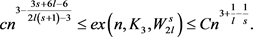
定理1.6：假设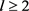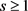，。令G是n个顶点的图，且边数为e，那么存在正数C，使得

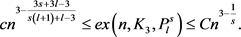
本文主要内容安排如下：第二节主要利用依赖随机选择技术证明一个相关引理；第三节证明主要定理。

2. 引理的证明

我们先利用依赖随机选择技术证明下述引理。

引理2.1：令a，m，r，n都是正整数。G是一个n个顶点的图，且图G中的边数为e，将图G中三角形的个数记为k，如果存在正整数t，使得

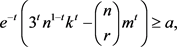
那么图G中存在一个大小至少是a的子集U，使得集合U中任意r个顶点在图G中至少含有m条公共邻边。

证明：令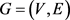是一个n个顶点，边数为e的简单图，且图G中有k个三角形。我们将图G的顶点集记为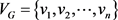：，边集记为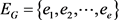：。首先，我们将从图G的边集中依均匀分布的可重复的选择t条边组成集合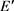，记为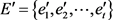。令X表示这t条边的所有公共邻点的集合，个数记为。

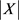我们做如下标记：

，

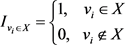那么，的期望值为：

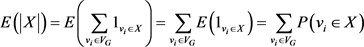
又因为

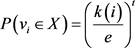
其中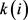，表示包含点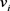的所有三角形的个数。

所以，

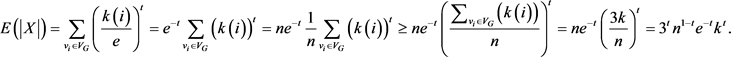
令R表示集合X中由r个顶点构成的r元-子集。如果R在图G中的公共邻边小于m条，就称R是“坏”的r元-子集。令Y表示集合X中所有“坏”的r元-子集，个数记为。令Z表示图G中的所有“坏”的r元-子集。

同样地，我们也做如下标记：

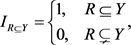
那么，可以得到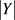的期望值为：

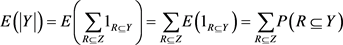
又因为R是Y中的r元-子集，且R在图G中的公共邻边小于m条，那么

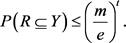
所以，

我们利用期望的线性，就可以得到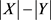的期望值为：

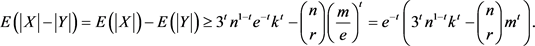
那么根据引理的条件得到：。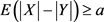

所以在图G中必定存在一种边集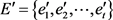的选择，使得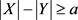成立。那么令U是从X中的每个“坏”的r元-子集中删除一个顶点得到的集合，那么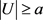，并且U中任意r个点在图G中至少有 条公共邻边。

3. 主要定理的证明

引理3.1：假设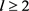，。令G是n个顶点的图，且边数为e，那么存在足够大的正数C，使得

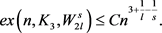
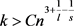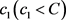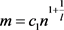证明：假设图G中三角形的个数，那么根据引理2.1，令，，，并且存在足够大的正整数，使得。又因为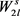的色数为3，根据Erdős-Stone定理，所以图G的边数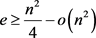。通过计算，我们可以得到：

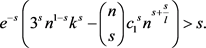(1)

(1)式的推导过程详见附录。所以在图G中存在一个大小至少是s的子集U，使得U中任意s个点在

图G中至少含有条公共邻边。又根据定理1.2，那么在U的一个s集的公共邻边中一定存在一个2l

长的偶圈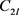，并且这2l条边都与这s个顶点相连。所以在图G中就可以找到一个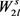的复制，与图G中不包含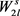矛盾。

引理3.2：假设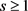，。令G是n个顶点的图，那么存在正数c，使得

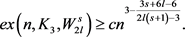
证明：从图G中按概率p随机地选择一条边，其中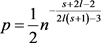。用X表示图G中的所有三角形构成的集合，个数记为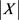。那么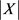的期望值为：

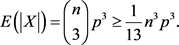
令Y表示图G中所有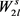构成的集合，个数记为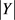，同样的，的期望值为：

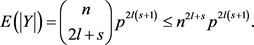
接下来，从图G中的一个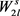中删除一条边，至多删除个三角形，那么将图G中所有的都删除一条边，至多就删除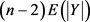个三角形，所以，

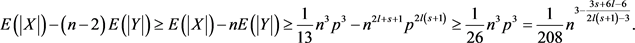(2)

(2)式中不等式成立是因为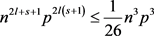，即：

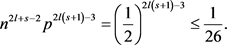
所以存在一个n个顶点的图G，使得图G中没有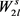的复制，但三角形的个数为。

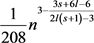我们利用引理3.1和引理3.2就完成了定理1.5的证明。

引理3.3：假设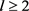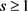，。令G是n个顶点的图，且边数为e，那么存在足够大的正数C，使得

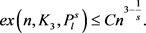
证明：与定理3.1的证明类似，假设图G中三角形的个数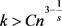，根据引理2.1，令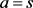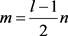，，，。同样的，因为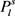的色数为3，所以图G的边数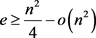。通过验证，可以得到：

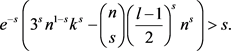(3)

(3)式的推导过程详见附录。所以在图G中可以找见一个大小至少是s的子集U，使得U中任意s个

点在图G中至少含有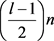条公共邻边。又根据定理1.1，那么在U的一个s集的公共邻边中一定存在

着一条l长的路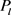，使得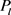上的边都与这s个点相连。所以在图G中一定可以找到一个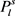的复制，与图G中不包含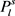矛盾。

引理3.4：假设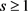，。令G是n个顶点的图，那么存在正数c，使得

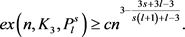
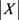证明：从图G中按概率p随机地选择一条边，其中，用X表示图G中的所有三角形构成的集合，个数记为。那么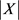的期望值为：

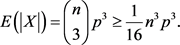
令Y表示图G中所有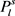构成的集合，个数记为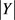，同理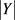，的期望值为：

同样地，从图G中的一个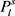中删除一条边，至多删除个三角形，那么将图G中所有的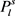都删除一条边，至多删除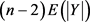个三角形，所以，

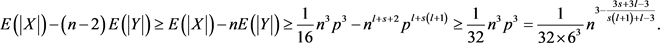(4)

(4)式中不等式成立是因为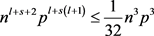，即：

所以可以找到一个n个顶点的图G，使得图G中没有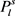的复制，但三角形的个数为。

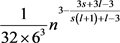同样的，利用引理3.3和引理3.4完成定理1.6的证明。

基金项目

本文得到了中国自然科学基金(11671296)和山西省优青青年学术带头人项目支持。