1. 引言
本文在一维有界区间上研究了如下可压缩变指数增长非牛顿流体模型的初边值问题,
(1)
带有初边值条件:
(2)
其中
分别表示密度,速度和压力。
为已知函数,
为定常数。
此类变指数增长流体模型通常用来描述电粘性流体的流动。1949年Winslow [1] 发现电粘性流体的特性是能够根据提供的电场强度来改变流体的粘性,作为一种新功能材料,广泛运用于可变减震器、喷墨印刷机、消振装置、离合器、阀、密封等,特别倾向于振动控制方面的应用。
当p(x)是常数,模型为带有Carreau’s Law结构的可压缩非牛顿流模型,关于强解的存在唯一性有很多结果见 [2] [3] [4]。当p(x)为函数时,Rajagopal,Růzǐčka [5] 首先得到了不可压缩流体模型,该模型由质量、线动量、角动量、能量的一般平衡定律、克劳修斯–杜赫不等式形式的热力学第二定律和Minkowskian形式的麦克斯韦方程导出。Růzǐčka在 [6] 中对其强解进行了进一步的研究。Diening [7] 对于不可压电粘性流体的理论和数值结果做了研究。还有很多关于变指数增长抛物型方程的结果可以在 [8] [9] [10] 中找到。由于模型强的非线性性和奇异性,对于变指数增长模型的研究,特别是,可压缩变指数非牛顿流体的研究还比较单薄,需要我们进一步探索。
本文研究的主要结论如下:
定理1:假设
满足
(
为常数),且具有一阶连续导数,初值条件
满足
(3)
和相容性条件:
(4)
则存在
,使得问题(1)~(2)存在唯一强解
满足
(5)
本文共有三节,在第二节中,我们将通过迭代的方法构造逼近方程,得到逼近解的先验估计,得到初值远离真空时,模型强解的存在性。应用第二节得到的与密度下界无关的一致先验估计,定理一的证明在第三节完成。
2. 先验估计
在这一部分,我们将考虑初值远离真空的情形。假设初始密度具有正的下界,通过迭代的方法构造了初边值问题(1)~(2)的逼近问题,并得到逼近解与密度下界无关的一致能量估计。
2.1. 逼近解的构造
首先,我们假设
足够光滑具有正的下界,即存在一个正数
使得
。接下来,我们运用文献 [11] 中迭代方法构造逼近方程并得到逼近解,
• 定义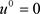 。
。
• 对
,给定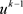 ,则根据一阶双曲守恒律(见 [12])和p(x)-Laplace抛物型方程(见 [8])的存在性理论,得到如下初边值问题具有唯一的强解
:
,则根据一阶双曲守恒律(见 [12])和p(x)-Laplace抛物型方程(见 [8])的存在性理论,得到如下初边值问题具有唯一的强解
:
(6)
(7)
满足如下初边值条件
(8)
其中
且满足相容性条件(4)。
2.2. 一致能量估计
本小节中,我们将对问题(6)~(8)的解
进行一致先验估计。
为了得到
的估计,我们定义函数
:
(9)
其中
是一个足够大的正整数。为了表述方便,定义下文中C为与
以及
有关常数。
下面,我们将估计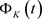 中的每一项。
中的每一项。
引理1 假设
是方程(6)~(7)的光滑解,存在
使得
对任意
成立。
证明:用
乘以(7)式两端,然后关于变量x在[0,1]上积分有
(10)
对于(10)关于变量t在
上积分,我们可以得到,
(11)
应使用Sobolev不等式和Young’s不等式,有
(12)
接下来依次估计
。应用Sobolev不等式和Young’s不等式,我们可以计算
将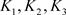 的估计代入(12),有
的估计代入(12),有
(13)
引理1的证明完成。
引理2:若 是(6)~(7)的解,那么存在
,使得
是(6)~(7)的解,那么存在
,使得
证明:对(7)关于t求导有
(14)
将方程(14)两端同乘以
然后在(0,1)上关于x积分,可以得到
(15)
因为
,我们可以计算
 (16)
(16)
另一方面,应用质量守恒方程(6)有
(17)
由(15)、(16)和(17),得到如下不等式,
(18)
应用Sobolev不等式,Hȍlder不等式和Young’s不等式,我们可以估计
。
其中
为与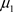 有关的足够小的常数。将上述估计代入(18)中有:
有关的足够小的常数。将上述估计代入(18)中有:
(19)
接下来,我们估计
。将方程(7)两端同乘以
,然后在
上关于x积分,由方程
(6)和分部积分,我们得到
(20)
我们首先计算方程(20)左端的第三项,
将上式代入(20),有
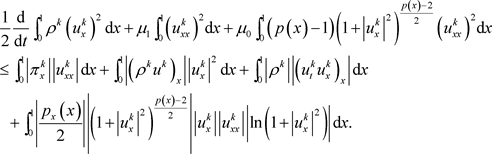 (21)
(21)
为了估计(21),我们需要仔细计算上式右端第四项。应用Hȍlder不等式和Young’s不等式,我们可以得到
 (22)
(22)
其中
和
。把(22)代入(21),应用方程(6)有
(23)
应用Sobolev不等式和Young’s不等式,有
对于
和
,在Sobolev不等式的帮助下,我们可以推出
应用Sobolev嵌入定理和
,下式成立,
 (24)
(24)
类似(22)中的估计,我们可以得到
(25)
因此,联立(24)和(25),因为
,
,选取足够小的
,我们可以得到
的估计,
收集 的估计,带入(23),可以得到
的估计,带入(23),可以得到
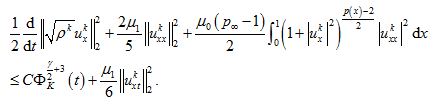 (26)
(26)
将(19)和(26)相加,可以得到
(27)
将上述不等式在
上积分,同时选取足够小的 ,对正整数
,我们有
,对正整数
,我们有
由相容性条件(4)、方程(7)和
的正则性,可以得到

由此,令
,我们可以得到
引理2证明完成。
引理3:假设
是方程(6)~(7)的解,存在
,对任意的
,
证明:用
乘以方程(6)两端,并关于x在
上积分,可以得到如下不等式
(28)
另一方面,(6)关于x求导后两边乘以
并关于x在
上积分,得
(29)
综合(28)和(29)式,有
(30)
由Gronwall’s不等式和引理1,上式可推得
(31)
引理3得证。
应用引理1~3和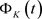 的定义可得
的定义可得
(32)
容易证明存在
,使得
因此,我们得到逼近解
的能量估计:对
,下式成立
3. 定理1的证明
在第二节中得到了逼近解的与密度下界无关的能量估计,应用 [2] 的方法,我们可以证明当
时,逼近解
强收敛,进一步可以证明极限
为问题(1)~(2)的唯一解,至此,我们完成了定理1的证明。
基金项目
由国家自然科学基金项目资助(No.11901379)。