1. 引言
1973年,Chvátal [1] 首次提出坚韧度的概念,用于研究图的哈密尔顿性。后来,坚韧度成为一个重要的网络抗毁性参数。
定义1 [1] 设G是一个非完全连通图,其坚韧度定义为
。
如果
,则称
为G的一个坚韧集,简称t-集。
定义2 [1] 设G是一个图,
为G的连通分支数。若对于G的任意点割集S,有
,其中t是正实数,则称图G是t-坚韧的。
Chvátal同时研究了图的坚韧度和哈密尔顿性的关系,提出了一个关于坚韧度的著名猜想:存在一个确定的正数
,任何
-坚韧图都是哈密尔顿图 [1]。2006年,Bauer在文献 [2] 中综述了坚韧度和周长的关系、2-坚韧猜想的反证明、因子、特殊图类、计算复杂度,以及与坚韧度相关的各种结果。
Broersm于1999年首次提出极小t-坚韧图的概念 [3]。
定义3 [3] 若图G的坚韧度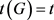 ,且每一个支撑真子图H的坚韧度
,则称G是极小t-坚韧的。
,且每一个支撑真子图H的坚韧度
,则称G是极小t-坚韧的。
换言之,删除G中任意一条边e,图G的坚韧度减小,就说这个图G是极小t-坚韧的。
Katona给出了一些极小t-坚韧图顶点度的上界,并证明了每个极小1-坚韧图的无爪图是一个圈 [4]。2018年,Katona等构造出几类特殊的极小t-坚韧图,并证明了,对于任意正整数t以及任意正有理数
,极小t-坚韧图的判定问题是DP-完备的 [5] [6]。
极小t-坚韧图具有重要的结构特性与研究意义,然而目前得到的极小t-坚韧图研究成果并不多。因此本文对极小t-坚韧图进行了研究,主要研究了几类笛卡尔积图和线图的极小t-坚韧性,并构造了一类k-正则的极小k/2-坚韧图。文中提及的图均为简单无向图,未加说明的概念和术语见文献 [7]。
2. 几类特殊的极小t-坚韧图
2.1. 笛卡尔积图的极小t-坚韧性
本节主要研究几类常见的笛卡儿积图,证明了完全图与完全图,路与圈的笛卡儿积图是极小t-坚韧的。
定义4设
和
是两个点不交的简单图,
和
的笛卡尔积
是一个简单图,其中
,并且对
,
,
,且
或者
且
。
引理1 [8] 设
是两个完全图的笛卡尔积,则
。
引理2 [9] 设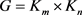 ,其中
,则
,其中
,则
1) G是
-正则的;
2) G是
-连通的。
定理1设
是两个完全图,则
是极小
-坚韧的。
证明由引理1知,
。再由引理2,容易知道,对
的任意一点
w,其邻点集即为
的一个t-集,且
,
。设
是
的任意一条边,记 ,则有
。令S为u在H中的邻点集,则有
,
。
,则有
。令S为u在H中的邻点集,则有
,
。
这表明
由定义3即得,
是极小
-坚韧的。
定理2设
,
分别表示路和圈,其中m为奇数,则
是极小
-坚韧的。
证明明显地,
是3-正则图。设
,
,且在
中,点i的邻点是
和
,其中
,并且关于模m同余。记
,则由
坚韧度的定义,易知
是
的一个t-集,
。设
是
的任意一条边,则在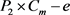 中,
均为2度点。因为
,
,所以有
。故结论成立。
中,
均为2度点。因为
,
,所以有
。故结论成立。
当
或m为偶数时,
,所以
不一定是极小t-坚韧图。
2.2. 轮形图的极小t-坚韧性
定义5设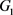 和
是两个点不交的图,
和
的联图,记为
和
是两个点不交的图,
和
的联图,记为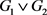 ,是指在
中将
的每个顶点与
的每个顶点之间用一条边连接起来所得到的图。
,是指在
中将
的每个顶点与
的每个顶点之间用一条边连接起来所得到的图。
定义6称
和
的联图
为轮形图,记为
。
中的点称为
的中心,与该点关联的边称为辐条。
定理3轮形图
是极小3/2-坚韧的。
证明由轮形图的结构易知,其中心和
上任意两个不相邻的点构成一个t-集,故有
。
对于任意的
,考虑以下两种情形。
情形1
。设
,则在
中,
均为2度点。因为
,所以
。
情形2
。用v表示e在圈
上的任一端点,v为2度点。与情形1同理,可知
。
综上所述,结论成立。
2.3. 线图的极小t-坚韧性
本节主要讨论三类线图的极小t-坚韧性,证明了路,圈,完全二部图的线图是极小t-坚韧的。
定义7一个图G的线图用
来表示,它的顶点集是G的边集,
中任意两点之间是相邻的,当且仅当G中对应的边是相邻的。
引理3 [5] 树T是极小
-坚韧的弦图。
定理4设
是n阶路,则其线图
是极小1/2-坚韧的。
证明由线图的定义,
是
阶的路。由引理3,
是极小1/2-坚韧的。
定理5设
是n阶圈,则其线图
是极小1-坚韧的。
证明由圈的结构和坚韧度的定义易知,n阶圈
是极小1-坚韧的。又因为
,所以
是极小1-坚韧的。
完全二部分图的线图
是两个完全图的笛卡尔积,因此有如下结论:
定理6设
是完全二部分图,则其线图
是极小
-坚韧的。
3. 一类极小t-坚韧正则图的构造
本节以轮形图为基础,构造了一类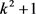 阶的k-正则的极小k/2-坚韧图。
阶的k-正则的极小k/2-坚韧图。
定义8设
是轮形图,将中心点之外的每个顶点都用一个k阶团替换,记这些团为
,任意两个团
和
之间恰有一条边相连,每个团中的每个顶点有且仅有一个邻点不在这个团中。将所得到的图记为
,则
是
阶的k-正则图。图1给出的是一个例子
。
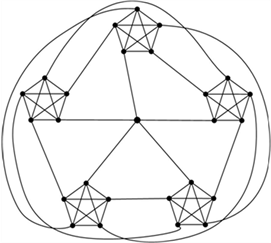
Figure 1. A 5-regular graph
with order 26
图1. 一个26阶的5-正则图
定理7由定义8所构造的图
是
阶k-正则的极小k/2-坚韧图,其中
。
证明因为
是
阶k-正则图,则对
的任意一点u,其邻点集
为
的一个t-集,且
,
,即
。设
是
的任意一条边,则在
中,
。令S为u在
中的邻点集,则
,
。易知S是
的一个t-集,从而
。
所以,
是极小k/2-坚韧的。
4. 总结
坚韧度是用来刻画网络抗毁性的一个重要参数。坚韧度与图的结构、哈密尔顿性结合的研究一直是图论中的热点问题。本文证明了几类笛卡尔积图和线图是极小t-坚韧的,并且构造出一类k-正则的极小k/2-坚韧图。极小t-坚韧图是大量存在的,但是找到这些图比较困难。有关极小t-坚韧图的构造与分类,仍有很多问题值得深入研究。