1. 引言
由Cahn和Hilliard在1958年提出的Cahn-Hilliard方程,常用于描述二元合金在某种不稳定状态时相的分离和粗化现象 [1]。粘性Cahn-Hilliard方程是由Novick Cohen等人 [2] [3] 在研究带粘性的二物质相互扩时提出,主要描述在冷却两种溶液如合金、玻璃及聚合物的混合体时出现的粘性相变。
关于Cahn-Hilliard方程的建模,算法,推导和计算方法已经被广泛研究。值得注意的是,设计高效、准确的数值方案是必须的。其中,显式格式通常会导致严重的时间步长限制,而且通常不满足能量衰减特性;隐显格式的优点是是求解常系数代数方程,能使得求解更容易实现 [4] [5] [6]。然而,半隐式格式通常具有较大的截断误差,因此需要较小的时间步骤来保证精度和能量稳定性。另一方面,满足能量稳定性和较小截断误差的隐式格式,主要缺点是需要在每个时间步长上求解非线性系统。
针对粘性Cahn-Hilliard方程的四阶导数和非线性特点,基于文 [7] [8] 提出的稳定的二阶隐显格式,我们研究了混合有限元的Crank-Nicolson/Adams-Bashforth (CN/AB)格式。本文要研究的粘性Cahn-Hilliard方程如下:
(1.1)
其中
是有界区域且具有光滑边界
,n表示边界上
的单位外法向量,u是两
相物质之一的浓度,参数
是一个与界面厚度有关的参数,
是粘性系数。其中函数
满足如下条件 [9]:即存在一个常数L,有
(1.2)
其中,
是双势阱函数。该方程的自由能被定义为
(1.3)
2. 预备知识
首先我们引入一些记号。
表示标准的Sobolev空间并且范数定义为
。
和
分别表示
上的内积和范数。定义
。
式(1.1)的混合变分形式为:
(2.1)
令
为
的拟一致三角剖分,h为空间网格大小,
为定义在
上的分段多项式空间:
,其中
是次数不超过r的多项式空间。
我们引入Ritz投影算子
,满足:
(2.2)
并且算子满足如下不等式 [10]:
(2.3)
定义截断误差
,其中
(2.4)
(2.5)
并且满足如下不等式 [11]:
(2.6)
(2.7)
3. 二阶Crank-Nicolson/Adams-Bashforth格式
将时间区间
剖为:
,
,N是一个正整数。全离散格式逼近问题(2.1)可以表述为下述方程,给定
,求
,有
其中
,
,
是时间步长。
定理3.1 设
是格式(3.1)-(3.2)的解,在
条件下,该格式是稳定的并且满足下面的能量法则:
证明 在(3.1)中取
,有
(3.3)
在(3.2)中取
,有
接下来我们对
进行估计,
利用公式
,则
利用泰勒公式,则
结合(3.3)和以及对的估计,有
(3.4)
利用Cauchy-Schwarz不等式和(1.2),即等式(3.4)的右边项有:
(3.5)
根据能量函数(1.3)的定义,结合(3.4)和(3.5),该定理得证。
定理3.2 设
和
分别是方程(2.1)和方程(3.1),(3.2)的解。且假设
,
,
,
,则满足下述估计式
证明:首先给一些符号
然后全离散格式利用上面的关系可以写成下面的等价式:
(3.6)
(3.7)
在(3.6)中分别取
以及在(3.7)中取
得到三个等式,对其求和有,
(3.8)
接下来,我们对
进行估计,其中
利用Cauchy-Schwarz不等式,Young不等式有,
利用截断误差(2.6)和(2.7),Cauchy-Schwarz不等式,Young不等式有,
对于
的估计,利用泰勒展示,Young不等式有,Cauchy-Schwarz不等式,有
综上,将
不等式带入(3.8)可以得到,
(3.9)
将(3.9)式两端n从0到
求和,可得
限制
,利用离散Gronwall引理和
定义,可得
利用三角不等式和Ritze投影算子(2.3),有
最终,则可得
,即
,定理得证。
4. 数值实验
在本部分,采用数值实例验证理论分析的正确性和有效性。在下面的算例中,用
元构建有限元空间,选择参数
,
,
,
,计算区域为
,初始条件为:
表1~3列出了全离散格式在范数
和范数
下的误差估计和收敛阶,可以观察到空间收敛阶在
范数下趋向于2.0,在
范数下趋向于1.0,与理论结果一致。其次,为了证明格式的稳定性,我们假设最
终时间
,时间步长
,
,
,图1观察到能量是随时间递减的。最终,我们分别刻画了图2~4在时间
时数值解的等值线
,
,观察数值解的变化过程,随着时间的推移,最终等值线会达到一个稳定。

Table 1. Numerial results for the spatial discretization for time step τ = 0.0001 , ( P 1 , P 1 ) mixed finite
表1. 固定时间步长
,
混合有限元空间收敛阶

Table 2. Numerial results for the spatial discretization for time step τ = 0.0001 , ( P 1 , P 1 ) mixed finite
表2. 固定时间步长
,
混合有限元空间收敛阶

Table 3. Numerial results for the spatial discretization for time step τ = 0.0001 , ( P 1 , P 1 ) mixed finite
表3. 固定时间步长
,
混合有限元空间收敛阶
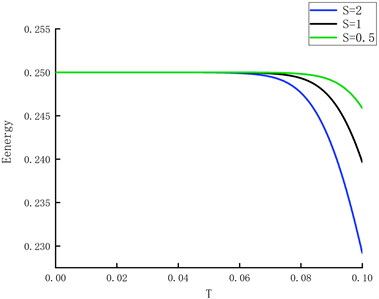
Figure 1. The evolution of the discrete energy for the viscous Cahn-Hilliard equation for
, s = 0.5, 1, 2
图1.
, s = 0.5, 1, 2时,粘性Cahn-Hilliard方程的能量演变
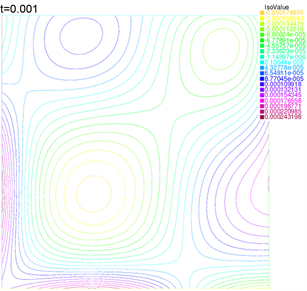
Figure 2. The contour lines at
图2. 当
时的等值线

Figure 3. The contour lines at
图3. 当
时的等值线
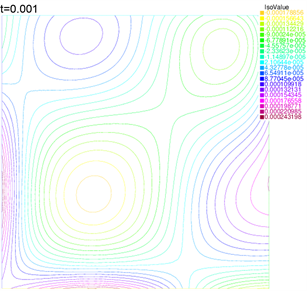
Figure 4. The contour lines at
图4. 当
时的等值线
5. 结论
本文研究了粘性的Cahn-Hilliard方程线性CN/AB格式混合有限元方法,达到了二阶收敛阶。最后,通过数值算例对理论分析进行验证,算例结果与理论分析的结果相一致。
基金项目
国家自然科学基金项目(NO. 11172194);山西省自然科学基金(NO. 201801D121016)。