意杨旋切板胶合木箱型梁受弯性能试验研究

Experimental Study on Flexural Performance of Poplar Laminated Veneer Lumber Box Beam

摘要: 箱型梁具有强度高、自重轻和受力性能良好等特点。本文将新型工程木意杨LVL与箱型截面形式相结合，研究意杨旋切板胶合木箱型梁受弯性能。通过八组意杨LVL箱型梁和一组实心梁的试验，以翼缘、腹板厚度、梁跨度为变量，对其力学性能、破坏形态等展开研究。分析不同因素对箱型梁承载力的影响，试验结果表明腹板和翼缘厚度对箱型梁受弯性能影响最大，LVL箱型梁出现底部受拉区拉断、腹板翼缘错层和腹板与翼缘拉断等三种破坏形式；经对比数据分析，推算出的箱型梁极限弯矩值与试验实测值较为吻合；旋切板胶合木箱型梁拥有较好的受力性能及较高的利用率，是一种能够适用于建筑结构的工程构件。

Abstract: Box girder has the characteristics of high strength, light weight and good mechanical performance. This paper combines LVL of new engineering Poplar with box section form to study flexural performance of poplar veneer box girder. Eight groups of Yiyang LVL box girders and one group of solid beams were tested. The mechanical properties and failure modes of flange, web thickness and beam span were studied. The influence of different factors on the bearing capacity of box girders is analyzed. The test results show that the thickness of web and flange has the greatest influence on the flexural performance of box girders. LVL box girders have three failure modes, i.e. bottom tension zone rupture, web flange staggered layer and web and flange rupture. Through comparative analysis, the ultimate bending moment of box girders is calculated. The results are in good agreement with the measured values. The plywood box girder with rotary cutting board has better mechanical performance and higher utilization ratio, and it is a kind of engineering component which can be applied to building structures.

1. 引言

21世纪，国家追求经济发展的同时更注重环境保护，国务院先后出台多项政策推行绿色建筑 [1]，为木结构的发展带来了新的机遇 [2]。旋切板胶合木是新型工程材的一种，是利用小径级原木旋切胶合而成，具有出材率高、强度高、变异性小、尺寸不受限制等优点，而意杨山东等地资源丰富，为意杨LVL的生产和应用提供了持续和可靠地保障 [3]。

目前国内外针对木材实心构件或工字型构件的研究较多。刘伟庆 [4] [5] 等以LVL为原材料，研究了复合木梁的受弯性能，得出LVL梁的结构性能远超出锯材构件；肖岩、官亚鹏 [6] [7] 对胶合竹工字梁进行抗弯性能试验，发现其强度一般由腹板的性能控制，翼缘竹材应变未能达到极限值。吕博 [8] 将两根U型钢与四块竹胶合板通过粘合剂粘接成一种箱型梁的形式，通过试验研究不同参数情况下组合箱型梁受弯性能；李卓霖 [9] 使用ABAQUS有限元分析软件，建立了三维非线性有限元模型利用正交分析原理，分析了不同参数对梁性能的影响大小，推算出优化组合箱型梁受弯性能的最佳参数；尚澎、孙友富 [10] 通过3根实心梁和15根空心梁胶合木梁对胶合木空心梁进行了抗弯性能试验研究，得出空心胶合木梁具有三种破坏模式，特点是梁底部受拉面产生拉伸破坏，具有脆性破坏特征的结论。而箱型构件作为一种强重比较高且基于工程木的构件，却鲜有学者对其进行研究。

相较于传统实心截面，当梁采用箱型截面时由于剔除了中间受力较小的部分，梁材料整体的利用率得到了很大的提高。LVL作为一种新型的工程木材，具有强度高、规格灵活、稳定性好等优点。大量的意杨资源以及稳固的政策支持，给意杨LVL在国内的发展带来了新的机遇和可靠地保障。

本课题将受力性能良好的箱型梁和材料性能良好的LVL材料结合在一起，设计出了八组LVL箱型梁和一组LVL实心梁，通过对LVL物理力学试验的研究、LVL箱型梁受弯试验的研究、理论分析和有限元模拟来分析其受力性能，建立一套LVL箱型梁的设计理论。此项研究成果将为意杨LVL箱型梁在木结构建筑中的应用提供理论依据。

2. 试件与方法

2.1. 试件设计

本试验试件参照《木结构设计规范》(GB50005-2003) [11]、《工程木结构设计规范》(DG/TJ 08-2192-2016) [12]、《木结构试验方法标准》(GBT 50329-2012) [13]、《木结构设计手册(第三版)》 [14] 及其他相关国内外规范进行设计并制作了9组试件，本试验试件生产加工全过程在江苏泗阳久和木业公司完成，其中包括8组箱型梁试件(以下简称XL1~XL8)和一组实心梁试件(以下简称SXL)。箱型梁部分主要设计了三种变量：腹板厚度d、翼缘厚度δ、梁跨度l。试件参数见表1，试件截面形式见图1。箱型梁中翼缘处LVL单板方向均为水平方向，腹板处LVL单板方向均为竖直方向。

2.2. 材料性能

本试验前期进行了材料物理力学性能试验 [15] - [23] 研究，所得参数见表2。

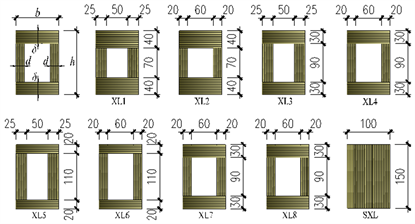
Figure 1. Section diagram of LVL box girder

图1. LVL箱型梁截面示意图

Table 1. Specimen parameters

表1. 试件参数

Table 2. Physical and mechanical parameters of specimens

表2. 试件物理力学参数

Figure 2. Layout of test components

图2. 试验构件测点布置图

2.3. 加载方案及测点布置

试验采用小型反力架作为试验加载装置，梁采用简支形式，加载点为试件的三分点处，在加载点下方垫有刚性垫块以防止局部受压破坏；使用液压千斤顶手动分级加载，每级荷载为2 kN，5~10 min之内达到最大荷载 [13]。试验分别在梁支座处、加载处和跨中处设置了五个位移计，用以量测梁的挠度；在梁侧面跨中截面处沿高度均匀设置了5片应变片，用以量测梁弯曲应变并验证平截面假定；在梁底面跨中截面出设置了1片应变片，用以量测梁极限拉应变。试验开始前需要对梁进行预加载，以确保各仪器均能正常使用，试验装置及测点布置见图2。

3. 试验结果及分析

3.1. 试验现象

构件在加载初期，材料基本处于弹性状态，荷载–位移曲线基本呈直线上升；当荷载加至15~20 kN时，构件开始发出较为明显的开裂声音，同时荷载–位移曲线不再保持直线变化；最终箱型梁构件主要呈现三种破坏形态，第一种为梁底受拉破坏，图3(a)，典型试件为XL3、XL4、XL7；第二种为腹板和翼缘均发生受拉破坏，图3(b)，典型试件为XL5、XL6、XL8，这些试件的主要特征为翼缘板较薄且同时腹板也较薄，当试件承受荷载时，胶缝连接处有较大的正应力，且随着荷载的增加，挠度逐渐增大，试件梁下部线条被不断拉长产生较大形变，从而导致腹板被拉裂；第三种为腹板与翼缘交界处错层，图3(c)，典型试件为XL1、XL2，这两个试件的主要特征为翼缘较厚，当试件承受荷载时胶缝连接处产生较大的剪应力，从而导致胶结失效，出现错层；图3(d)，实心梁构件的破坏形态则为脆性受拉破坏。

(a) 箱型梁底部受拉破坏 (b) 箱型梁腹板、翼缘受拉破坏 (c) 腹板、翼缘错层破坏 (d) 脆性受拉破坏

Figure 3. Failure modes of components

图3. 构件破坏形态

3.2. 试验结果

试验结果列于表3。其中包括构件开裂荷载，极限荷载，极限挠度与计算所得的抗弯弹性模量。所有试件的荷载–位移曲线见图4。

从图4中可以分析，试件的破坏可以分为二个阶段，第一阶段内试验梁基本呈现出完全线弹性工作状态，挠度增长速率稳定。到达第二阶段时，梁表现在为弹塑性工作状态直至破坏。随着荷载的增长，试验梁刚度逐渐退化，挠度增长明显，此时梁内部木纤维已经逐步产生损伤，发出细碎的撕裂声。随着外荷载的增加，裂缝持续发展，试验观察分析，一旦木纤维拉断声响变得密集，梁很快便形成肉眼可见的裂缝，并迅速贯穿受拉区跨中底板，造成脆性破坏。对于大部分梁试件而言，完全弹性工作阶段可以持续达到破坏荷载的80%左右，且梁进入第二阶段时虽然荷载–位移曲线斜率有所减小，但是并不十分明显，可见其刚度退化不多，典型代表有XL3、XL4、XL5、XL6、XL8。对于少数梁而言，由于存在初始缺陷，在进入第二破坏阶段之后曲线斜率明显减小，挠度增长速度快，刚度大幅度退化，典型代表有XL1、XL2、XL7。

Table 3. Test results

表3. 试验结果

注：I—试件截面惯性矩，P_cr—开裂荷载，P_u—破坏荷载，ω—挠度，E—弹性模量。

Figure 4. Load deflection curve

图4. 荷载挠度曲线

3.3. 腹板厚度对抗弯性能的影响

通过XL1与XL2、XL3与XL4、XL5与XL6的试验结果进行腹板厚度对于箱型梁抗弯承载能力影响的分析见图5。

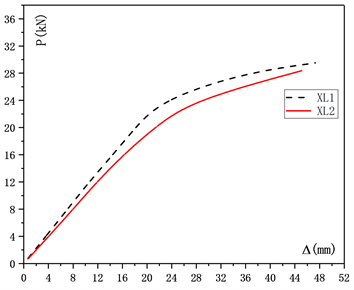
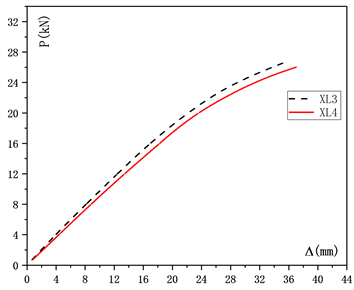
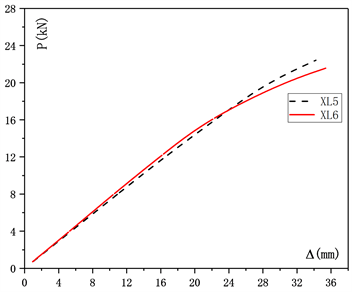
Figure 5. Load-curve contrast diagram of components with different web thickness

图5. 不同腹板厚度构件荷载–位移曲线对比图

相同翼缘厚度、不同腹板厚度的箱型梁构件的荷载位移曲线形状以及平滑程度基本相同，且LVL箱型梁抗弯刚度随着腹板厚度的减小而减小，随着箱型梁腹板厚度的减小，试验梁的极限承载能力减小，其减小幅度较小，对比XL1与XL2、XL3与XL4、XL5与XL6，其减小幅度分别为：3.9%、3.0%、3.8%。抗弯刚度在初期基本维持稳定不变，随着荷载的增加逐渐减小。

3.4. 翼缘厚度对抗弯性能的影响

通过XL1、3、5与XL2、4、6的试验结果进行翼缘厚度对于箱型梁抗弯承载能力影响的分析见图6。

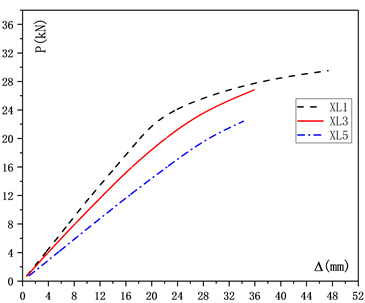
Figure 6. Load curve comparison of different flange thickness members

图6. 不同翼缘厚度构件荷载–位移曲线对比图

相同腹板厚度、不同翼缘厚度的箱型梁构件的荷载应变曲线形状以及平滑程度基本相同。随着箱型梁翼缘厚度的减小，试验梁的极限承载能力减小，其减小幅度相对较大，对比XL1与XL3与XL5、XL2与XL4与XL6，其减小幅度分别为9.0%与14.9%、8.3%与15.7%，从整体趋势而言，箱型梁的抗弯刚度会随着翼缘厚度的减小而减小；抗弯刚度在试验初期基本维持稳定，随着荷载的增加逐步出现刚度退化的情况。对于XL2而言，在试验初期其抗弯刚度就与XL4的抗弯刚度相差不多，这是由于XL2节点处存在初始缺陷，导致其抗弯刚度的退化。

3.5. 跨度对抗弯性能的影响

通过XL4、7、8的试验结果进行不同跨度对于箱型梁抗弯承载能力影响的分析见图7。

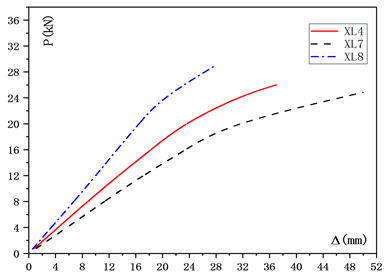
Figure 7. Load curve comparison of different flange thickness members

图7. 不同跨度构件荷载–位移曲线对比图

相同空心率、不同跨度的箱型梁构件的荷载位移曲线形状基本相同，但抗弯刚度有着明显的区别。从上图可以看出，随着箱型梁跨度的增大，试验梁的抗弯刚度将减小，对比XL8、XL4、XL7，其减小幅度分别为4.0%和2.9%；XL7的抗弯刚度最小，XL4次之，XL8最大。由此可见，箱型梁的抗弯刚度会随着跨度的增大而减小，相较于XL8，XL7的抗弯刚度减小53.3%，XL4的抗弯刚度减小33.4%。

3.6. 箱型梁的平截面假定

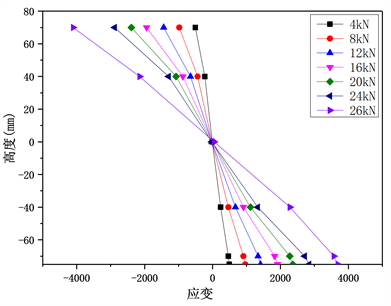
Figure 8. The relationship between load and strain of middle span of typical box girders (XL4)

图8. 典型箱型梁跨中截面承受荷载与应变的变化关系图(XL4)

随着外荷载的逐渐增加，LVL箱型梁跨中的挠度变形逐渐增加，梁截面的应变同样逐渐增大。各级荷载作用下的LVL箱型梁跨中截面上应变沿截面高度的分布示意图如图8所示。由图可知，在加载过程中，随着荷载的增加，LVL箱型梁跨中截面上的应变沿高度基本保持线性比例关系，符合平截面假定。图中可知，试件接近破坏时，受拉区木纤维的最大拉应变达到了4000 με左右，受压区木纤维的最大压应变达到了4300 με左右。

4. 理论分析与讨论

4.1. 挠度计算

挠度是结构正常使用极限设计的重要参考指标。木材由于其抗弯刚度较其他材小，往往当其达到限定挠度时其极限承载力还远未达到，因此在进行箱型梁结构设计的时候，挠度变形控制应作为重要设计要点。

LVL箱型梁挠度计算公式为：

${\omega }_x=\frac{23P{a}^3}{48EI}$ (1)

式中： ${\omega }_x$ ——理论挠度；P——弹性阶段的承载力；a——加载点到支座的距离，本文中为1/3；EI——构件抗弯刚度。

根据木结构设计规范中表4.2.7的规定，木结构中受弯构件的挠度限值为1/250。表4中， $\omega$ 表示挠度实测值， ${\omega }_x$ 表示理论挠度。根据式(1)推算出正常使用极限状态下构件的承载力P，并从荷载—挠度曲线中找到P所对应的挠度值即为在正常使用阶段的试验挠度值 $\omega$，得到 ${\omega }_x/\omega$ 的值。

表4为箱型梁挠度规范允许值与实测值对比，从表4可以看出，箱型梁的试验挠度与理论挠度吻合良好，其误差控制良好均在10%以内，能够满足实际工程的需要。

Table 4. Deflection measured values and allowable values of specifications

表4. 挠度实测值与规范允许值

4.2. 极限承载力计算

LVL箱型梁的破坏形式呈现为脆性破坏，主要由木纤维拉断所导致，因此本文中LVL箱型梁极限承载力采用极限应变法进行计算分析。在计算中假定构件符合平截面假定，且假定木材受拉时为理想的弹性体，受压时为理想的弹塑性体，采用的胶合木材本构模型 [24] 见图9，则其应力应变关系如式2、3所示。

受压区：

${\sigma }_{\text{c}}=\{\begin{array}{l}E{\epsilon }_{\text{c}},0\le {\epsilon }_{\text{c}}\le {\epsilon }_{\text{ce}}\\ f_{\text{ce}},{\epsilon }_{\text{ce}}\le {\epsilon }_{\text{c}}\le {\epsilon }_{\text{cu}}\end{array}$ (2)

受拉区：

${\sigma }_{\text{t}}=E{\epsilon }_{\text{t}}$ (3)

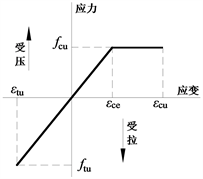
Figure 9. Stress-strain curve of glued wood

图9. 胶合木材应力–应变曲线

箱型梁受弯时，若其到达破坏时一直保持在线弹性状态，受压区高度 $h_{\text{c}}=\frac{h}{2}$，则极限弯矩：

$M_{\text{u}}=W{f}_{\text{tu}}$ (4)

若箱型梁破坏时已经进入塑性状态，则其截面的应力应变分布见图10。

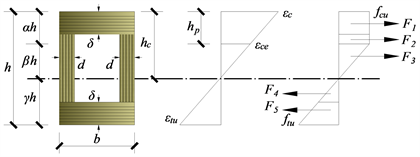
Figure 10. Diagram of Stress-Strain Distribution of Solid Beam section

图10. 实心梁截面的应力应变分布示意图

图中：h_c为梁受压区高度、h_p为梁塑性受压区高度。将梁截面划分为塑性受压区、弹性受压区、受拉区三段，并引入高度系数，分别为 $\alpha$ 、 $\beta$ 、 $\gamma$，则塑性受压区高度为 $\alpha h$，所产生的拉力为F₁；弹性

受压区高度为 $\beta h$，所产生的压力为F₂；受拉区高度为 $\gamma h$，所产生的压力为F₃。令 $m=\frac{{\epsilon }_{\text{tu}}}{{\epsilon }_{\text{cu}}}=\frac{f_{\text{tu}}}{f_{\text{cu}}}=\frac{\gamma h}{\beta h}$。

$\{\begin{array}{l}{F}_1=f_{\text{cu}}\cdot \delta \cdot b\\ F_2=f_{\text{cu}}\cdot \left(\alpha h-\delta \right)\cdot 2d\\ F_3=\frac{1}{2}\cdot f_{\text{cu}}\cdot \beta h\cdot 2d\\ F_4=\left(\gamma h-2\delta +\frac{{\delta }^2}{\gamma h}\right)\cdot f_{\text{tu}}\cdot d\\ F_5=f_{\text{tu}}\cdot \delta \cdot b-\frac{f_{\text{tu}}\cdot b\cdot {\delta }^2}{2\gamma h}\end{array}$ (5)

由力及截面力矩的平衡求得箱型梁极限弯矩为：

$\begin{array}{c}{M}_{\text{u}}=F_{\text{1}}\cdot \left(\alpha h+\beta h-\frac{1}{2}\delta \right)+F_{\text{2}}\left[\beta h+\frac{1}{2}\left(\alpha h-\delta \right)\right]+F_{\text{3}}\cdot \frac{2}{3}\cdot \beta h\\ +F_{\text{4}}\cdot \frac{2}{3}\left(\gamma h-\delta \right)+F_{\text{5}}\cdot \left[\gamma h-\frac{3\gamma h\cdot \delta -2{\delta }^2}{3\left(2\gamma h-\delta \right)}\right]\end{array}$ (6)

将LVL箱型梁极限弯矩计算值M_u与试验实测值M相比较(表5)，可以看出，梁极限弯矩计算值与实测值较为吻合，误差范围为仅有2.3%~4.8%，证明此理论公式适用于LVL箱型梁的设计模型。

Table 5. Comparisons between calculated and measured ultimate bending moments

表5. 极限弯矩计算值与实测值对比

5. 结论

本文通过控制箱型梁腹板厚度、翼缘厚度、跨度的变化设计了八根箱型梁和一根实心LVL梁，并对其进行试验研究和理论分析。从试验结果分析，得出以下主要结论：

1) 各箱型梁试件在加载过程中出现响声的荷载相差不多，基本都处于15 kN~20 kN之间，箱型梁出现响声之后不久试验梁即将破坏；实心梁达到响声荷载之后试验梁仍然能够持续承载一段时间才至破坏荷载。对于箱型梁而言，其翼缘厚度对于承载力的影响比腹板厚度对于承载力的影响更大；当箱型梁截面尺寸固定时，随着箱型梁跨度的增大，试验梁的抗弯刚度将减小；

2) 从试验结果可以看出当其达到受弯极限承载能力，出现梁底受拉破坏时，其挠度已经远远超出了规范所规定的允许挠度值，达到了允许值的3~5倍。分析了正常使用极限状态破坏值与承载力极限状态破坏值的比值P/P_u，对比不同跨度的箱型梁，发现跨度越大，P/P_u值越大；对比箱型梁和实心梁，发现同跨度下实心梁的P/P_u值远大于箱型梁，说明箱型梁较实心梁而言能够更大限度的利用材料的性能。

3) 结合试验现象和荷载位移曲线，发现箱型梁设计中，腹板和翼缘厚度取值非常重要，合理的取值范围将大大提高箱型梁受弯性能；试验发现，当翼缘厚度取为1/5h、腹板厚度取为1/3~5/6δ时，箱型梁的抗弯弹性模量较大，破坏形态也更符合常规木构件的破坏形态，具有较好的受弯性能。

4) 在计算中发现，抗拉强度与抗压强度的比值m大致会随着空心率的增大而减小，可见空心率的大小会影响着箱型梁内部的应力分布。

从以上研究可以看出，旋切板胶合木箱型梁拥有较好的受力性能及较高的利用率，是一种能够适用于建筑结构的工程构件。

基金项目

多重荷载下意杨旋切板胶合木新型楼盖受力性能(51878590)。

NOTES

^*通讯作者。