1. 引言
随着世界油气资源的日渐枯竭,深水领域已成为油气资源主要采集区 [1]。作为油气田运输生命线的海底管道,其铺设安装技术是亟待解决的难题。其中能否使船与管线触地点间的有效距离能够得到合理控制是铺管作业成功与否的关键。因此,对动力定位条件下船舶在波浪中的时域运动进行仿真分析是有必要的。
船舶在波浪中的运动作为船舶与海洋工程领域的经典问题,国内外很多学者都对其进行了深入研究。国外学者Cummins [2] 最早提出时域理论,把船舶运动在各时刻的响应看做相互叠加的脉冲相应作用,并由Ogilvie [3] 对时域理论进行了推广并将其应用于有航速船舶的计算中。此后,国内外大量学者将时域理论与仿真分析相结合进行研究,如国外的Debabrata等 [4] 三维有航速船舶大幅运动进行了时域仿真研究并对以往线性计算进行了优化。国内的陈京普 [5] 等也采用了计及非线性项影响的时域数值仿真方法对船舶的运动进行了仿真分析。同时大量学者对基于动力定位的海洋结构物运动进行了深入研究,如国外的Holvik和Morgan [6] 等研究了动力定位系统在深海半潜式平台的应用。国内的林峰 [7] 等采用了简易的PID动力定位系统,对S型铺管船的铺管工况进行了耦合运动分析。
本文基于船舶时域运动方程,采用应用最为广泛的PID及Kalman滤波相结合的动力定位系统,对铺管船在波浪中的运动与控制进行分析与研究。
2. 铺管船时域运动方程
基于最经典的Cummins时域理论 [2],即把船舶的六自由度运动看成连续的脉冲响应相互叠加的结果,时域方程的计算过程就是在频域下计算得到船舶的附加质量和阻尼系数,然后通过傅里叶变换将其转换为船舶时域运动方程的基本参数,建立船舶的时域运动响应分析方程。本文以海洋石油201船为研究对象,根据卡明斯理论在考虑波浪载荷的情况下,建立海洋石油201船的时域运动方程:
(1)
上式中M为船舶质量矩阵,
表示频率为无穷大时的附加质量,t为船舶运动时间,
为时延函数,
为船舶运动位移矩阵,B为粘性阻尼系数矩阵,
和t为时刻之间的任意运动时间,C为恢复力系数矩阵;F(t)为外环境载荷矩阵。
3. 铺管船波浪力计算
波浪力包括一阶波浪力和二阶漂移力。一阶波浪力是由入射波引起的,包括由未受干扰的波浪场引起的傅汝德–克雷洛夫力和由与船体结构有关的修正波场引起的绕射力。二阶波浪力由于其频率易与船体低频响应运动发生共振,因此会对船体运动产生很大影响。船体在波浪中运动受到的波浪载荷的水平分量即为二阶漂移力,在二阶漂移力的作用下,无约束的漂浮船体会随波浪作低频漂移运动。本文中将利用衍射分析和已定义的波谱密度函数求得频率传递函数,进而计算一阶和二阶总波浪力及力矩。
为验证不规则波对铺管船运动的影响,本文采用“北海联合海浪计划”中提出的Jonswap谱作为不规则波浪输入 [8]。由系数A、系数B、谱峰周期Tp和有义波高Hs定义的Jonswap波谱密度可以表示为:
(2)
式中指数q的计算公式为:
(3)
式(2)中S(ω)为谱密度函数,A为广义菲利普斯常数,ω为波浪分量的圆频率,ωp为谱峰处的圆频率。
菲利普斯常数A可以表示为:
(4)
参数σ可以表示为:
(5)
峰值参数B可以定义为:
(6)
本文选取了包括不同有义波高和谱峰周期在内的四种海况,这四种海况与Jonswap谱的对应关系如图1所示。
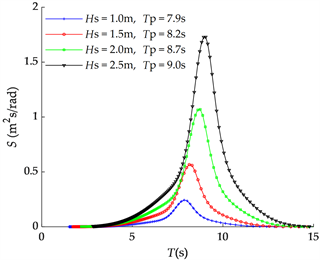
Figure 1. Jonswap spectrumfor four sea states.
图1. 四种海况对应的Jonswap谱
不规则海况可以通过叠加原理来建立(叠加原理是一个问题可以分解成有各自解的不同子问题,且整个问题的解是各个子问题的解的总和),即不规则波可以通过将多个频率
和波幅
的波分量叠加得到。当波浪的整体运动具有n个波分量时,波浪的速度势可以表示为:
(7)
式中h为水深,ki代表波数,βi代表主波浪的传播方向,ɛi代表波浪的相位角。
通过谱密度函数S(ω)和波浪的传播函数D(βi)能够求得波浪的波幅:
(8)
则一阶波浪力在时域内的表达式为:
(9)
式中
为波高和激振力之间的一阶传递函数,在本文中使用WAMIT软件进行计算 [9]。
二阶传递函数(QTF)用于计算线性波浪漂移力,其表达式为:
(10)
上式中的
即为二阶传递函数(QTF),同样由WAMIT软件求得。
4. 铺管船控制模型
PID (比例–积分–微分)控制器在工程中广泛应于模拟铺管船的位置。在动力定位的过程中,PID控制器读取位置信号,将其与目标值作比较,通过运算,得到抵消位置偏差和外界干扰力所需要的推力,然后对推力器发出指令,以产生能够使船尽可能靠近预期位置的推力。PID控制器的非线性水平位置反馈控制器为:
(11)
式中
代表推进器所需推力,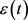 表示位置误差,
为位置反馈增益,
为所需积分反馈增益,
为速度反馈增益,
为前馈风力,
为目标位置,
为所需滤波位置。
表示位置误差,
为位置反馈增益,
为所需积分反馈增益,
为速度反馈增益,
为前馈风力,
为目标位置,
为所需滤波位置。
当船舶在波浪中运动时,其运动成分中含有低频分量(LF)和高频分量(HF),推进器控制的是其中的低频分量部分。在实际中由于高频成分会经过放大并传到推进器,因此DP系统对速度和位置信号中的高频分量很敏感。为解决这一问题,使用卡尔曼滤波器对位置和速度进行修改。首先基于位置参考系对船舶运动进行定位并与目标位置进行比较,然后使用卡尔曼增益矩阵对先前预测的位置进行修改。其中卡尔曼增益矩阵与截止频率有关,截止频率是由运动的自然持续时间和波频运动决定的 [10]。
5. 铺管船控制模型
5.1. 模型参数
本文的研究对象是海洋石油201船主要参数如表1所示。

Table 1. The parameters of the HYSY201
表1. 海洋石油201船主要参数
5.2. 不同有义波高下铺管船时域运动仿真分析
为了仅探讨不同有义波高对船体运动的影响,本文忽略海流对船体运动的影响并采用Jonswap谱模拟随机波浪载荷,本节中所用的波浪与船舶横剖面夹角为45˚,谱峰周期5 s。考虑到可以进行作业的浪级,有义波高分别取1 m,1.5 m,2 m和2.5 m。本节四种工况下铺管船运动与推力曲线如图2所示。
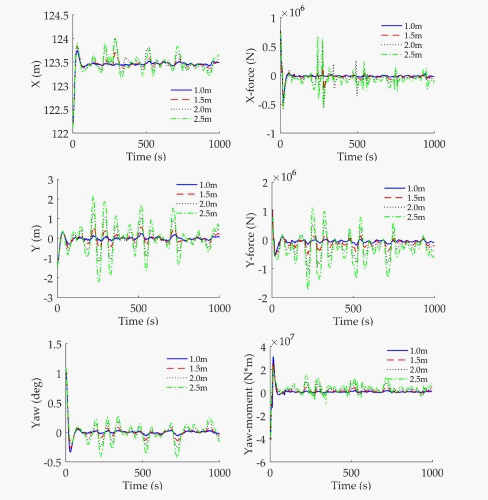
Figure 2. Dynamic response and thruster force of HYSY201
图2. 海洋石油201船运动与推力曲线
计算结果表明,在动力定位条件下,铺管船在到达目标位置过程中的运动和推进器输出的推力会瞬间增大,在经过一段时间运动后趋于动态的稳定状态,并且在较小的范围内运动,可以看出船舶在稳定后能够保持较好的定位;船舶的运动趋于动态的稳定时,动力定位系统对船舶的推力(矩)也趋于稳定。达到动态稳定后,当有义波高分别为1.0 m,1.5 m,2.0 m和2.5 m时,纵荡运动最大值分别为123.52 m,123.7 m,124.01 m和123.98 m;横荡运动绝对值最大值分别为0.3437 m,0.5796 m,1.32 m和2.147 m;首摇运动绝对值最大值分别为0.0584 deg,0.1433 deg,0.2633 deg和0.4199 deg。达到稳定状态后,纵向推力绝对值分别为6.94 × 104 N,2.28 × 105 N,5.65 × 105 N和6.64 × 105 N;横向推力绝对值分别为1.82 × 105 N,5.02 × 105 N,1.05 × 106 N和1.72 × 106 N。结合图像能够看出达到动态稳定状态后,有义波高的改变对铺管船运动的动态平衡位置没有影响,但会影响铺管船在平衡位置附近的振动幅度且随着有义波高的增大运动会更为剧烈。推进器输出推力会随着有义波高的增大而增大,且在同一工况下推进器输出推力的变化趋势与船舶运动响应变化趋势大体相符。
5.3. 不同谱峰周期下铺管船时域运动仿真分析
本节中采用的波浪与船舶横剖面夹角为45˚,有义波高2 m。考虑到可以进行作业的浪级,分别选取谱峰周期为5 s,6 s,7 s和8 s。本节四种工况下铺管船运动与推力曲线如图3所示。
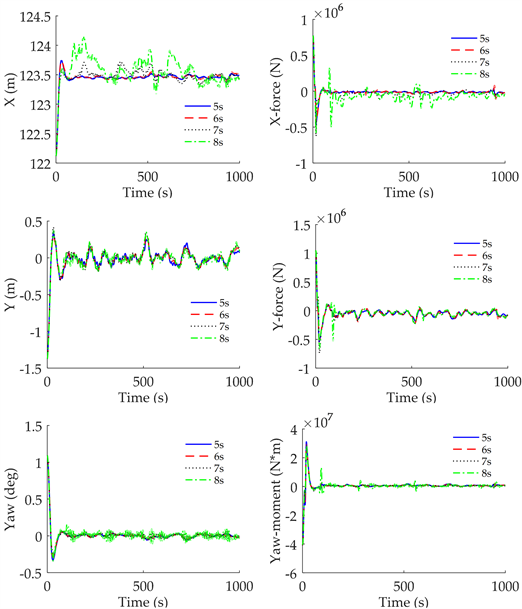
Figure 3. Dynamic response and thruster force of HYSY201
图3. 海洋石油201船运动与推力曲线
从图中能够看出,不同周期下铺管船的运动在到达目标位置后,均有趋于动态稳定的趋势。达到动态稳定后,当谱峰周期分别为5 s,6 s,7 s和8 s时,纵荡运动最大值分别为123.52 m,123.55 m,123.711 m和154.6 m;横荡运动绝对值最大值分别为0.23 m,0.3087 m,0.344 m和0.352 m;首摇运动绝对值最大值分别为0.0341 deg,0.0409 deg,0.0744 deg和0.1505 deg。达到稳定状态后,纵向推力绝对值分别为3.2 × 104 N,5.33 × 104 N,9.31 × 104 N和1.08 × 105 N;横向推力绝对值分别为1.82 × 105 N,2.15 × 105 N,2.22 × 106 N和2.33 × 106 N。可见在本节四种工况下随着谱峰周期的增大,铺管船在平衡位置附近的振荡幅度和推进器输出的推力均会变大。需要注意的是铺管船的纵荡运动,在波浪方向为45˚的情况下,从图中能够看出当周期增大到一定程度时,铺管船的纵荡运动会稍微偏离正常轨迹,推进器输出的推力也会大幅增加,因此在实际作业中应尽量规避在谱峰周期过大的海况下作业。
6. 结论
针对铺管船在波浪中的时域运动,建立了由状态空间模型来近似代替卷积分项的铺管船时域运动方程,并采用PID及Kalman滤波相结合的动力定位系统,对铺管船在波浪中的时域动力定位进行仿真模拟。分别对不同有义波高和不同谱峰周期下的铺管船运动响应及推力分配进行了计算分析,得到结论:1) 在本文工况下,动力定位系统对船舶的运动能起到很好的控制作用,铺管船在稳定位置附近振动幅度很小,有较好的作业工况适应性;2) 在动力定位条件下,一定范围内有义波高的改变不会影响铺管船的平衡位置,但铺管船在平衡位置的振荡幅度和推进器输出的推力会随有义波高的增大而增大;3) 谱峰周期对铺管船运动的影响与有义波高相似,但当谱峰周期增大到一定程度时,会对船舶纵荡运动的平衡位置产生一定影响。
基金项目
国家科技重大专项(2016ZX05057020),深圳市“十三五”海洋经济创新发展示范项目(3818),中国海洋石油集团有限公司科技项目(CNOOC-KJ 135 GJJS 07 GC 2020-02)。