基于数据预处理和支持向量回归的PM_2.5、NO₂和SO₂组合预测研究

Research on Combined Forecasting of PM_2.5, NO₂and SO₂ Based on Data Preprocessing Technology and Support Vector Regression

摘要: 由于空气污染能够引起多种呼吸道非传染性疾病，甚至造成生命质量受损或者过早死亡，所以空气污染已经成为全球死亡人数增加的第二大原因，因此，制定合理且有效的空气污染治理措施已经迫在眉睫。预测在空气污染预警过程中扮演着重要的角色，准确且科学的预测能够帮助人们有效规避空气污染的危害，因此，提高预测的精度与科学性也成为众多学者关心的问题之一。本研究为了提高空气污染预测的准确性，采用了数据预处理互补集合经验模式分解(complementary ensemble empirical mode decomposition, CEEMD)技术、支持向量回归(support vector regression, SVR)、广义回归神经网络(general regression neural network, GRNN)和粒子群优化(particle swarm optimization, PSO)算法建立组合模型。通过PM_2.5、NO₂和SO₂时间序列数据检验建立的组合预测模型的有效性，根据平均绝对百分比误差(mean absolute percentage error, MAPE)发现：组合预测模型能够提高PM_2.5、NO₂和SO₂指标的预测精度，如西安市的SO₂指标，最优单项模型的MAPE值为6.13%，而组合模型的MAPE值为5.86%。总之，组合预测模型能够为空气污染治理提供更准确的预测信息，为空气污染的防控提供理论支持。

Abstract: Because air pollution can cause a variety of respiratory non-communicable diseases, and even lead to impaired quality of life or premature death, the air pollution has become the second leading cause of the increase in deaths worldwide. Therefore, it is extremely urgent to formulate reasonable and effective air pollution control measures. Prediction plays an important role in the early warning process of air pollution. Accurate and scientific predictions can help people avoid the hazards of air pollution effectively. Therefore, how to improve the accuracy and scientificity of prediction has become one of the concerns of many scholars. To improve the accuracy of air pollution prediction, this study adopts data preprocessing technology complementary ensemble empirical mode decomposition (CEEMD), support vector regression (SVR), general regression neural network (GRNN), and particle swarm optimization (PSO) algorithms to establish a combined model. By PM_2.5, NO₂ and SO₂ index time-series data set checking the validity of combined forecasting model, according to the mean absolute percentage error (MAPE), it is found that the combined model can improve the prediction accuracy of PM_2.5, NO₂ and SO₂ index. For example, the MAPE of the optimal individual model and the combined model of the SO₂ index is 6.13% and 5.86% respectively in Xi’an. In short, the combined prediction model can provide more accurate prediction information for air pollution control and provide theoretical support for air pollution prevention and control.

1. 引言

空气污染是由能够改变空气自然特性的化学性、物理性的气体或者固体组成的混合物对室内外环境造成的污染，其主要污染物包括：颗粒物(细颗粒物，PM_2.5和粗颗粒物，PM₁₀)、臭氧(O₃)、二氧化硫(SO₂)、一氧化碳(CO)和二氧化氮(NO₂) [1]。根据世界卫生组织报道，城市、郊区和农村的空气污染每年大约导致全球500万人死亡，仅次于吸烟 [2]。Wang Y.等 [3] 研究了31个城市的空气污染状况，结果发现绝大多数城市中占比最大的空气污染成分都是PM_2.5。此外，PM_2.5暴露是慢性阻塞性肺疾病(COPD)、下呼吸道感染、脑血管等疾病的重要影响因素 [4]。NO₂进入人体后能形成硝酸和亚硝酸，并对肺组织产生剧烈的刺激从而引起肺炎、COPD等疾病 [5]。Khaniabadi Y.等 [6] 研究了霍拉马巴德地区的SO₂发现SO₂的浓度与急性心梗和COPD住院人数的增加呈正相关。

空气污染对人类健康的危害越来越严重，其中主要是由于空气污染物浓度的增加，如PM_2.5、NO₂和SO₂，所以降低空气污染物水平已经成为改善人类健康的重要措施。根据中国环境空气质量标准的规定，PM_2.5、NO₂和SO₂一级标准的年平均限值分别为15 μg/m³、40 μg/m³和20 μg/m³，二级标准分别为35μg/m³、40 μg/m³和60 μg/m³；PM_2.5、NO₂和SO₂平均24小时的一级标准为35 μg/m³、80 μg/m³和50 μg/m³，二级标准为75 μg/m³、80 μg/m³和150 μg/m³ [7]。为了有效地降低空气污染物水平，减少过早死亡的发生，因此相关部门需要尽快制定更合理的环境管理措施，而空气污染预测作为一种科学的空气质量预警技术，其预测信息能够指导相关部门制定改善空气质量的措施。王建州等的研究指出：组合预测模型结合了不同单项预测模型的优点，能够更准确地预测空气污染趋势 [8]。因此本文基于互补集合经验模式分解(complementary ensemble empirical mode decomposition, CEEMD)、支持向量回归(support vector regression, SVR)和广义回归神经网络(general regression neural network, GRNN)建立组合模型，该模型的权重由粒子群优化算法(particle swarm optimization, PSO)搜索获得。PM_2.5、NO₂和SO₂数据的预测结果表明，所建立的组合模型优于单项模型。

2. 方法

2.1. 互补集合经验模式分解

基于EMD在分解非线性、不平稳信号的优势和EEMD解决“模式混合”问题的特点提出了CEEMD方法 [9]。以兰州市的NO₂为例，用CEEMD分解图如图1所示，具体过程如下：

第一步，在原始信号x的基础上添加一对相反的白噪声信号 $n_t$，得到具有正负信号的噪声序列 $x_t^{+}$ 和 $x_t^{-}$，

$\left[\begin{array}{c}{x}_t^{+}\\ x_t^{-}\end{array}\right]=\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]\left[\begin{array}{c}x\\ n_t\end{array}\right]$

第二步，将噪声信号用CEEMD分解为 $IM{F}_{d,t}^{+}$ 和 $IM{F}_{d,t}^{-}$，重复κ次，其中 $IM{F}_{d,t}$ 是第t次的第d个本征模态函数(intrinsic mode function, IMF)。

第三步，计算由正负信号分解的IMFs的均值，其中 $\overline{T_{\kappa }}$ 是指CEEMD分解的IMFs的均值，

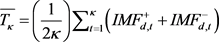
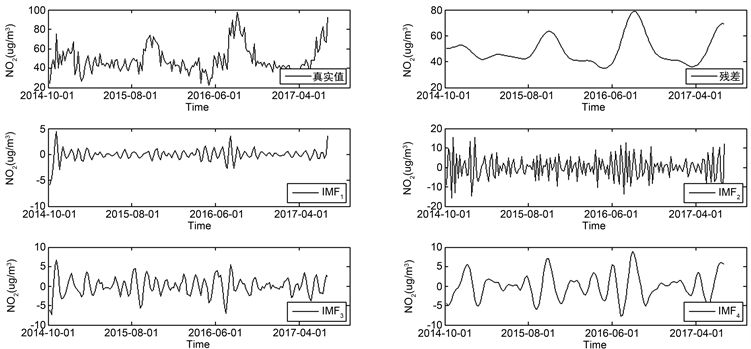
Figure 1. The true series and decomposition series of NO₂ indicator in Lanzhou

图1. 兰州市NO₂的真实序列和分解序列

2.2. 支持向量回归

回归的基本思想是指给定训练样本，使得样本的拟合值与真实值尽可能接近。由于样本的不规则性和非线性，传统的回归方法使得拟合值与真实值之间存在较大误差，因此，本文运用优化算法优化SVR拟合由CEEMD分解的IMF和残差序列。支持向量回归的基本思想是将样本数据通过一个非线性映射 $\varphi$ 映射到高维特征空间，并在这个高维特征空间中进行线性回归 [10]，即

$f\left(X\right)=\omega \varphi \left(X\right)+b$

$\varphi :R^l\to R$

其中b是阈值， $\omega$ 是权向量，l是维数，X是影响因素矩阵。 $ϵ$ 支持向量回归机与传统回归的区别是：当模型输出的 $f\left(X\right)$ 与真实y之间的损失大于偏差 $ϵ$ 时计算损失。

$\varphi (·)$ 定义之后，采用 $ϵ$ 不敏感损失函数并引入松弛变量 ${\xi }_i$ 和 ${\xi }_i^{\text{*}}$，于是SVR问题就转换为:

$\underset{\omega }{\min }1/2{\Vert \omega \Vert }^2+C\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\left({\xi }_i+{\xi }_i^{*}\right)$

$\text{s}\text{.t}\text{.}f\left(X_i\right)-y_i\le ϵ+{\xi }_i^{*}$

$y_i-f\left(X_i\right)\le ϵ+{\xi }_i$

${\xi }_i,{\xi }_i^{*}\ge 0$

其中C是误差惩罚参数，它的作用是平衡模型复杂性和经验风险，其对SVR的性能也有很大影响。解决上述凸优化问题可以引入拉格朗日函数将其转化为对偶问题解决，即

$f\left(X\right)=\underset{i=1}{\overset{n}{{\displaystyle \sum }}}\left({\hat{\alpha }}_i-{\alpha }_i\right)\kappa \left(X,X_i\right)+b$

其中 ${\alpha }_i$ 和 ${\hat{\alpha }}_i$ 是拉格朗日乘子， $\kappa \left(X,X_i\right)$ 为核函数，本研究中采用高斯核函数：

$\kappa \left(X,X_i\right)=\exp \left(-g{\Vert X-X_i\Vert }^2\right)$

其中g为核参数。由于核参数(g)与误差惩罚参数(C)对于预测结果存在一定影响，因此我们引入优化算法寻得最优的参数 [11]。

Mirjalili S.和Hashim S. [12] 基于鸟群的觅食行为提出PSO，该算法的基本思想是在搜索空间中通过更新fitness寻得最优全局解。Sarafrazi S.和Nezamabadi-pour H. [13] 基于万有引力定律，即搜索空间中质量越大的粒子具有更大的吸引力，提出重力搜索算法(gravitational search algorithm, GSA)。本研究主要运用PSO和GSA算法的快速局部收敛优势和开发能力寻得SVR模型的最优核参数(g)与误差惩罚参数(C)，并利用PSO算法搜索组合预测中单项模型的最优权重。

2.3. 广义回归神经网络

Specht D. [14] 在1991年提出一种具有非线性映射能力且学习收敛速度快的GRNN模型，其简单的网络结构同时具有较好的容错性和鲁棒性。GRNN由输入层、模式层、求和层和输出层构成，如图2所示，其中输入层用来输入训练的样本数据，根据样本向量的维数确定神经元的个数；模式层的神经元相互独立且传递函数为径向基函数；求和层是对模式层各单元输出和各单元输出的加权值进行求和。

Figure 2. The structure of GRNN

图2. GRNN神经网络结构

2.4. 组合预测模型

将2014年10月1日~2017年12月31日的PM_2.5、NO₂和SO₂浓度的167个周数据分为训练集(1-122，122个周数据)、验证集(123-137，15个周数据)和测试集(138-167，30个周数据)。训练集数据用来优化IMF和lag的个数以获得高精度的单项模型，基于验证集数据用PSO算法搜索组合模型的权重，测试集数据用来测试组合模型的预测能力。

第一步，分解。CEEMD预处理方法将PM_2.5、NO₂和SO₂浓度的122个周数据分别分解为不同的低频 $IM{F}_i^{低}$ 、高频序列 $IM{F}_i^{高}$ 和残差序列。根据试错法选择合适的IMF个数和滞后阶数(lag)，

$y=IM{F}_i^{高}+IM{F}_i^{低}+残{差}_i$

第二步，拟合。高频和低频序列用PSO-SVR算法拟合获得 $\widehat{IMF}{}_i^{高}$ 和 $\widehat{IMF}{}_i^{低}$，残差序列分别用GRNN、PSOGSA-SVR、PSO-SVR、GSA-SVR算法进行拟合。将高频、低频和残差的拟合结果相加获得单项模型的预测值，

${\hat{y}}_M=\widehat{IMF}{}^{高}+\widehat{IMF}{}^{低}+\widehat{残差},M=1,2,\cdots ,48$

第三步，搜索权重。通过第一步和第二步为每个污染物选择三个精度最高的单项模型 ${\hat{x}}_1$ 、 ${\hat{x}}_2$ 和 ${\hat{x}}_3$，基于验证集数据(15个周数据)使用PSO优化算法在搜寻三个单项模型的最优权重 ${\hat{W}}^1$ 、 ${\hat{W}}^2$ 和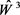。因此我们可以得到组合预测为：

$\hat{y}={\hat{W}}^1\cdot {\hat{x}}_1+{\hat{W}}^2\cdot {\hat{x}}_2+{\hat{W}}^3\cdot {\hat{x}}_3$

第四步，通过30个周数据测试建立的组合模型的效果。组合模型的建模过程如图3所示，以PM_2.5为例。

3. 结果

3.1. 预测评估指标

对建立的组合模型和单项模型用平均绝对百分比误差(mean absolute percentage error, MAPE)、均方误差(mean square error, MSE)、平均绝对误差(mean absolute error, MAE)和一致性指标(index of agreement, IA)进行评价。MAPE、MAE和MSE值越小，说明预测效果越好，IA是一种评价不同模型之间预测能力的无量纲指标，IA越接近1，模型的预测能力越好。分别定义如下：

$\text{MAPE}=\frac{1}{i}{\displaystyle {\sum }_{i=138}^{167}\left|\frac{y_i-{\hat{y}}_i}{y_i}\right|}$,

$\text{MSE}=\frac{1}{i}{\displaystyle {\sum }_{i=138}^{167}{\left(y_i-{\hat{y}}_i\right)}^2}$,

$\text{MAE}=\frac{1}{i}{\displaystyle {\sum }_{i=138}^{167}\left|y_i-{\hat{y}}_i\right|}$,

$\text{IA}=1-\frac{{\displaystyle {\sum }_{i=138}^{167}{\left(y_i-{\hat{y}}_i\right)}^2}}{{\displaystyle {\sum }_{i=138}^{167}{\left(\left|{\hat{y}}_i-\bar{y}\right|+\left|y_i-\bar{y}\right|\right)}^2}}$

其中 $y_i$ 是真实的浓度值，而 $y_i$ 分别表示预测值， $\bar{y}$ 是真实浓度的平均值。

Figure 3. The flow chart of the combined model

图3. 组合模型的流程图

3.2. 模型选择

本研究中IMF的个数(d)分别设置为2、3、4和5，滞后的阶数(lag)分别设置为3、4和5，对每个污染序列来说总共获得 $4\times 3\times 4=48$ 个单项模型。根据模型评价指标MAPE从48个单项模型中选择三个精度最高的模型，此外，由于气候条件、经济状况等方面的原因，最优单项模型的lag和IMF个数在不同城市的不同污染指标中表现不同，具体信息见表1，如兰州市PM_2.5的滞后的阶数为3，IMF的个数为5，而西安市滞后的阶数为3，IMF的个数为3。

Table 1. The number of Lag, IMF and the residuals of the three individual models

表1. 三个单项模型的lag、IMF个数和残差拟合的模型

注释：第一个参数是滞后的阶数，第二个参数表示分解的IMF的个数，第三个参数表示残差序列的预测模型，其中NN、P、G和PG分别表示GRNN、PSO-SVR、GSA-SVR和PSOGSA-SVR模型。

根据原始数据的特点与内在的价值，通过MAPE、MAE、MSE和IA值选择三个最优的单项预测模型；然后，基于三个最优单项模型用PSO算法寻得三个模型的权重值，见表2。从表2中可以看出单项模型的预测精度越高，PSO算法寻得权重值越大，如兰州市PM_2.5最优模型的MAPE值为4.44%，其权重为0.6372。

Table 2. The weights of three optimal individual model

表2. 三个最优单项模型的权重

3.3. 预测结果分析

组合模型与单项模型的MAPE值如表3所示，从表中可以发现：各城市不同指标的组合预测模型优于其最优的单项预测模型，说明组合模型不仅泛化性能较高，而且稳定性较高。此外，组合模型可以显著提高空气污染指标的预测精度，如西安市SO₂指标中最优单项模型是6.13%，组合模型为5.86%。表4是组合模型的MAE、MSE和IA值，从中可以看出组合模型的IA值都在0.95之上，说明组合模型总体预测效果较好。

Table 3. The MAPE of combined model and individual model

表3. 组合模型和单项模型的MAPE值

Table 4. The MSE, MAE and IA of combined model

表4. 组合模型的MSE、MAE和IA值

4. 结论

本研究提出组合预测模型对大气污染进行建模分析，并使用兰州市和西安市的PM_2.5、NO₂和SO₂浓度数据进行了验证和测试。为了提高组合模型的预测精度，使用了CEEMD方法对数据进行分解处理，即将原始数据分解为不同的低频和高频数据，这种处理方法显著提高了模型预测的准确性。此外，将机器学习方法(SVR)的参数用三种不同的算法进行了优化，结果发现不同城市不同指标的数据结构适用不同的优化算法。最后，基于所选择的最优单项模型，使用了PSO算法搜索出适合的权重值。数据分析结果表明组合模型的预测精度高于最优的单项模型。因此，组合预测模型能够为空气污染治理提供更准确的预测信息，为空气污染的防控提供理论支持。

基金项目

本研究在全国统计科学研究项目(2018LZ30)和2018年度教育部春晖计划项目资助下完成。

NOTES

^*通讯作者。