强n-Gorenstein FC-投射模

doi:10.12677/PM.2020.1010114

期刊菜单

强n-Gorenstein FC-投射模
Strongly n-Gorenstein FC-Projective Modules

DOI: 10.12677/PM.2020.1010114, PDF, HTML, XML, 国家自然科学基金支持
作者: 杨富霞^*, 张翠萍^#：西北师范大学数学与统计学院，甘肃兰州
关键词: FC-投射维数；Gorenstein FC-投射维数；强n-Gorenstein FC-投射模；FC-Projective Dimensions； Gorenstein FC-Projective Dimensions； Strongly n-Gorenstein FC-Projective Modules

摘要: 引入了强n-Gorenstein FC-投射模，给出了强n-Gorenstein FC-投射模的一些性质，证明了对任意模M和非负整数n，R-模M的Gorenstein FC-投射维数不超过n当且仅当M是强n-Gorenstein FC-投射模的直和因子时。

Abstract: In this paper, strongly n-Gorenstein FC-projective modules are introduced, some properties of them are presented. For arbitrary module M and nonnegative integral number n, the Gorenstein FC-projective dimensions of M are not larger than n if and only if M is direct summand of a strongly n-Gorenstein FC-Projective module.

文章引用：杨富霞, 张翠萍. 强n-Gorenstein FC-投射模[J]. 理论数学, 2020, 10(10): 974-979. https://doi.org/10.12677/PM.2020.1010114

1. 引言

1969年，在双边Noether环上，Auslander等在 [1] 中对有限生成模M引入了G-维数的概念(记为 $G {-dim}_{R} (M)$ )，证明了 $G {-dim}_{R} (M) \leq p d_{R} (M)$ 。1995年，Enochs等在 [2] 中证明了在双边Noether环上，G-维数为0的有限生成模与Gorenstein投射模等价，从此Gorenstein同调代数得到了广泛关注。2004年，Holm在 [3] 中对任意环，讨论了Gorenstein投射模和Gorenstein内射模及其维数，使得Gorenstein同调代数得到了极大的发展。2009年，Mahdou等在 [4] 中引入了强n-Gorenstein投射，内射，平坦模，给出了它们的基本性质和等价刻画，并证明了对任意模M和非负整数n，R-模M的Gorenstein投射维数不超过n当且仅当M是某个强n-Gorenstein投射模的直和项时。2013年，刘仲奎等人在 [5] 中将该结论做到了半对偶化模上。2013年，高等人在 [6] 中引入了强Gorenstein FP-内射模的概念，并研究了其相关同调性质，对偶于上述概念，2020年，王玉等人在 [7] 中引入了Gorenstein FC-投射模，2018年，他们又研究了强Gorenstein FC-投射模，得到了许多对偶的结论。

受以上工作的启发，本文主要研究强n-Gorenstein FC-投射模。证明了对任意模M和非负整数n，R-模M的Gorenstein FC-投射维数不超过n当且仅当M是某个强n-Gorenstein FC-投射模的直和项时。

本文所指的环R均指有单位元的结合环，模均指左R-模， $p d_{R} (M)$ 指M的投射维数， $i d_{R} (M)$ 指M的内射维数。

2. 预备知识

首先回顾一些基本概念。设n是非负整数，在 [8] 中，称R-模Q是n-余表现模，如果存在R-模的正合序列 $0 \to Q \to Q_{0} \to Q_{1} \to \dots \to Q_{n}$ ，其中每个 $Q_{i} (0 \leq i \leq n)$ 是有限余生成内射模。R-模Q是0-余表现模(1-余表现模)当且仅当Q是有限余生成的(有限余表现的)，每个 $(n + 1)$ -余表现模是n-余表现的，反之不一定成立。

定义2.1 [7] 设M是R-模，称M是FC-投射的，如果对任意的有限余表现左R-模Q，有 $E x t_{R}^{1} (M, Q) = 0$ 。

定义2.2 [7] 设M是R-模，称M是Gorenstein FC-投射的，如果存在FC-投射R-模的正合序列

$X = \dots \to P_{1} \to P_{0} \to P^{0} \to P^{1} \to \dots$

使得 $M ≅ K e r (P^{0} \to P^{1})$ ，且对任意内射维数有限的有限余表现R-模Q， $H o m_{R} (X, Q)$ 是正合的。

定义2.3 [9] 设M是R-模，称M是强Gorenstein FC-投射的，如果存在FC-投射R-模的正合序列

$X = \dots \overset{}{\to} P \overset{f}{\to} P \overset{f}{\to} P \overset{f}{\to} \dots$

使得 $M ≅ K e r f$ ，且对任意内射维数有限的有限余表现R-模Q， $H o m_{R} (X, Q)$ 是正合的。

对R-模M，记M的FC-投射维数为 $F C - p d_{R} (M)$ [7]，定义如下：

$F C - p d_{R} (M) = inf {n |$ 存在R-模的正合序列 $0 \to P_{n} \to P_{n - 1} \to \dots \to P_{0} \to M \to 0$ ，其中 $P_{i}$ 是FC-投射模， $0 \leq i \leq n}$ 。

如果这样的n不存在，记 $F C - p d_{R} (M) = \infty$ 。

记M的Gorenstein FC-投射维数为 $G F C - p d_{R} (M)$ [7]，定义如下：

$G F C - p d_{R} (M) = inf {n |$ 存在R-模的正合序 $0 \to G_{n} \to G_{n - 1} \to \dots \to G_{0} \to M \to 0$ ，其中， $G_{i}$ 是Gorenstein FC-投射模， $0 \leq i \leq n}$ 。

如果这样的n不存在，记 $G F C - p d_{R} (M) = \infty$ 。

下面我们引入强n-Gorenstein FC-投射模的概念。

定义2.4 设M是R-模，n是非负整数。称M是强n-Gorenstein FC-投射的，如果存在R-模的正合序列 $0 \to M \to P \to M \to 0$ ，其中 $F C - p d_{R} (P) \leq n$ 。且对任意内射维数有限的有限余表现R-模Q，有 $E x t_{R}^{n + 1} (M, Q) = 0$ 。显然，强Gorenstein FC-投射R-模是强0-Gorenstein FC-投射的。

3. 主要结果

称环R是左余凝聚的，如果每个1-余表现R-模是2-余表现的。以下R均是左余凝聚环。

命题3.1 设n是非负整数， $M_{i} (i \in I)$ 是R-模。如果对任意的 $i \in I$ ， $M_{i}$ 是强n-Gorenstein FC-投射的，那么 $\oplus_{i \in I} M_{i}$ 是强n-Gorenstein FC-投射的。

证明已知对任意的 $i \in I$ ， $M_{i}$ 是强n-Gorenstein FC-投射模，所以存在R-模的正合序列 $0 \to M_{i} \to Q_{i} \to M_{i} \to 0$ ，其中 $F C - p d (Q_{i}) \leq n$ ，且对任意内射维数有限的有限余表现R-模L，有 $E x t_{R}^{n + 1} (M_{i}, L) = 0$ ，因此有正合列 $0 \to \oplus_{i \in I} M_{i} \to \oplus_{i \in I} Q_{i} \to \oplus_{i \in I} M_{i} \to 0$ ，由( [7] 命题2.2)和( [7] 命题2.7)易得， $F C - p d (\oplus_{i \in I} Q_{i}) \leq n$ ，有 $E x t_{R}^{n + 1} (\oplus_{i \in I} M_{i}, L) ≅ \prod_{i \in I} E x t_{R}^{n + 1} (M_{i}, L) = 0$ 。故 $\oplus_{i \in I} M_{i}$ 是强n-Gorenstein FC-投射的。

命题3.2 设n是非负整数，M是R-模，如果M是强n-Gorenstein FC-投射的，那么M是强m-Gorenstein FC-投射的，其中 $m (\geq n)$ 是整数。

证明由已知存在正合序列 $0 \to M \to P \to M \to 0$ (1)，其中 $F C - p d_{R} (P) \leq n$ ，且对任意内射维数有限的有限余表现R-模L，有 $E x t_{R}^{n + 1} (M, L) = 0$ ，显然 $F C - p d_{R} (P) \leq m$ ，用 $H o m_{R} (-, L)$ 作用在(1)上，由( [7] 命题2.7)可得， $0 = E x t_{R}^{n + 1} (M, L) ≅ E x t_{R}^{n + 2} (M, L) ≅ \dots ≅ E x t_{R}^{m + 1} (M, L)$ ，故M是强m-Gorenstein FC-投射的。

命题3.3 设n是非负整数，M是R-模，如果M的FC-投射维数不超过n，那么M是强n-Gorenstein FC-投射的。

证明取正合序列 $0 \to M \to M \oplus M \to M \to 0$ ，由( [7] 命题2.2)和( [7] 命题2.7)得， $F C - p d_{R} (M \oplus M) \leq n$ ，且对任意内射维数有限的有限余表现R-模L， $E x t_{R}^{n + 1} (M, L) = 0$ 。

故M是强n-Gorenstein FC-投射的。

引理3.4 设n是正整数，M是强n-Gorenstein FC-投射模R-模，如果存在正合序列 $0 \to N \to P_{n} \to \dots \to P_{1} \to M \to 0$ ，其中 $P_{i}$ 是投射的 $(1 \leq i \leq n)$ ，那么N是强Gorenstein FC-投射的。

证明由已知存在R-模的正合序列 $0 \to M \to P \to M \to 0$ ，其中 $F C - p d_{R} (P) \leq n$ ，且对任意有限余表现R-模L，有 $E x t_{R}^{n + 1} (M, L) = 0$ ，考虑R-模的正合交换图：

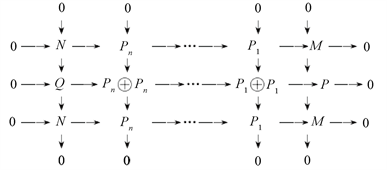
因为 $F C - p d_{R} (P) \leq n$ ，由( [7] 命题2.7)得，Q是FC-投射R-模，用 $H o m_{R} (-, L)$ 作用在正合序列 $0 \to N \to P_{n} \to \dots \to P_{1} \to M \to 0$ 上，可得 $E x t_{R}^{1} (N, L) ≅ E x t_{R}^{n + 1} (M, L) = 0$ 。由 [9] 推论3和以上交换图的第一列可得，N是强Gorenstein FC-投射的。

命题3.5 设n是非负整数，M是R-模，如果M是强n-Gorenstein FC-投射的，那么 $G F C - p d_{R} (M) \leq n$ 。

证明取R-模的正合列 $0 \to N \to P_{n} \to \dots \to P_{1} \to M \to 0$ ，其中 $P_{i}$ 是投射模， $1 \leq i \leq n$ 。由引理2.4知，N是强Gorenstein FC-投射的，从而N是Gorenstein FC-投射的，故 $G F C - p d_{R} (M) \leq n$ 。

称环R [7] 是左GFCP-闭的，如果Gorenstein FC-投射R-模对扩张是封闭的，即R-模的正合列 $0 \to N \to M \to Q \to 0$ ，如果N，Q是Gorenstein FC-投射的，那么M是Gorenstein FC-投射的。

设X是R-模的类， $y \subseteq X$ 。称y是X的生成子，如果对任意的 $x \in X$ ，存在R-模的正合列 $0 \to x^{1} \to y \to x \to 0$ ，其中 $y \in Y$ ， $x^{1} \in X$ 。

对偶地，可以定义X的余生成子。

显然，FC-投模类是Gorenstein FC-投射模类的生成子和余生成子。

由( [10] 定理5.5)可得以下结论。

引理3.6 设R是GFCP-闭左余凝聚环，M是R-模，n是非负整数，则以下条件等价：

(1) $G F C - p d_{R} (M) \leq n$ ；

(2) 存在R-模的正合列 $0 \to G_{n} \to G_{n - 1} \to \dots \to G_{1} \to G_{0} \to M \to 0$ ，其中 $G_{n}$ 是GFC-投射模， $G_{i} (0 \leq i \leq n - 1)$ 是FC-投射模；

(3) 存在R-模的正合列 $0 \to G_{n} \to G_{n - 1} \to \dots \to G_{1} \to G_{0} \to M \to 0$ ，其中 $G_{0}$ 是GFC-投射模， $G_{i} (1 \leq i \leq n)$ 是FC-投射模；

(4) 对任意的非负整数t， $0 \leq t \leq n$ ，存在R-模的正合列 $0 \to G_{n} \to G_{n - 1} \to \dots \to G_{1} \to G_{0} \to M \to 0$ ，其中 $G_{t}$ 是GFC-投射模，当 $i \neq t$ 时， $G_{t}$ 是FC-投射模。

引理3.7 设n是非负整数，M是R-模，如果 $G F C - p d (M) \leq n$ ，那么对任意的 $i > n$ 和任意内射维数有限的有限余表现模L，有 $E x t_{R}^{i} (M, L) = 0$ 。

证明由( [7] 引理2.3)和维数转移易得结论。

定理3.8 设R是左GFCP-闭环，n是非负整数，M是R-模。 $G F C - p d_{R} (M) \leq n$ 当且仅当M是某个强n-Gorenstein FC-投射模的直和项。

证明当 $n = 0$ 时，即证明M是Gorenstein FC-投射的当且仅当M是某个强Gorenstein FC-投射R-模的直和项。

( $\Rightarrow$ ) 设M是Gorenstein FC-投射R-模，则存在FC-投射R-模的正合序列

$X = \dots \overset{}{\to} P_{0} \overset{f_{0}}{\to} P_{1} \overset{f_{1}}{\to} P_{2} \overset{f_{2}}{\to} P_{3} \overset{}{\to} \dots$

使 $M ≅ K e r f_{0}$ ，且对任意内射维数有限的有限余表现R-模Q， $H o m_{R} (X, Q)$ 是正合的。记复形 $X$ 的m次平移为 $Σ^{m} (X)$ 。

$X = \dots \overset{}{\to} P_{0} \overset{f_{0}}{\to} P_{1} \overset{f_{1}}{\to} P_{2} \overset{f_{2}}{\to} P_{3} \overset{}{\to} \dots$

$Σ^{1} (X) = \dots \overset{}{\to} P_{1} \overset{f_{1}}{\to} P_{2} \overset{f_{2}}{\to} P_{3} \overset{f_{3}}{\to} P_{4} \overset{}{\to} \dots$

$Σ^{2} (X) = \dots \overset{}{\to} P_{2} \overset{f_{2}}{\to} P_{3} \overset{f_{3}}{\to} P_{4} \overset{f_{4}}{\to} P_{5} \overset{}{\to} \dots$

$\dots$

$Σ^{m} (X) = \dots \overset{}{\to} P_{m} \overset{f_{m}}{\to} P_{m + 1} \overset{f_{m + 1}}{\to} P_{m + 2} \overset{f_{m + 2}}{\to} P_{m + 3} \overset{}{\to} \dots$

对上述正合列作直和得正合列

$\oplus_{i \in I} Σ^{i} (X) = \dots \overset{}{\to} \oplus_{i \in I} P_{i} \overset{\oplus_{i \in I} f_{i}}{\to} \oplus_{i \in I} P_{i} \overset{\oplus_{i \in I} f_{i}}{\to} \oplus_{i \in I} P_{i} \overset{}{\to} \dots$

令 $N = K e r (\oplus_{i \in I} f_{i}) = \oplus_{i \in I} K e r (f_{i})$ ，则M是N的直和项， $H o m_{R} (\oplus_{i \in I} Σ^{i} (X), Q)$ $≅ \prod_{i \in I} H o m_{R} (Σ^{i} (X), Q)$ 是正合的，由( [7] 命题2.2)可得， $\oplus_{i \in I} P_{i}$ 是FC-投射的，从而N是强Gorenstein FC-投射模。

( $\Leftarrow$ ) 设N是强Gorenstein FC-投射R-模，M是N的直和项，则N是Gorenstein FC-投射的，由( [7] 推论4.5)可得，M是Gorenstein FC-投射的。

假设 $G F C - p d_{R} (M) \leq n \neq 0$ 。

( $\Rightarrow$ ) 由引理3.6知，存在R-模的正合列 $0 \to K \to G \to M \to 0$ ，其中G是Gorenstein FC-投射模， $F C - p d_{R} (K) \leq n - 1$ ，从而有R-模的正合列 $0 \to G \to P \to G^{0} \to 0$ ，其中P是FC-投射R-模， $G^{0}$ 是Gorenstein FC-投射R-模，考虑 $G \to M$ 和 $G \to P$ 的推出图 [11]：

由正合列 $0 \to K \to P \to D \to 0$ 知， $F C - p d_{R} (D) \leq n$ ，设M的Gorenstein FC-投射分解为 $0 \to G_{n} \to P_{n} \to \dots \to P_{1} \to M \to 0$ ，其中 $P_{i}$ 是FC-投射模 $(1 \leq i \leq n)$ ， $G_{n}$ 是Gorenstein FC-投射的，令 $G_{i} = K e r (P_{i} \to P_{i - 1})$ ，其中 $P_{0} = M$ ， $i \geq 1$ ，则有

$0 \to G_{1} \to P_{1} \to M \to 0$

$0 \to G_{2} \to P_{2} \to G_{1} \to 0$

$\dots$

$0 \to G_{n} \to P_{n} \to G_{n - 1} \to 0$

且 $G F C - p d_{R} (G_{i}) \leq n - 1$ ， $1 \leq i \leq n$ 。

设 $G_{n}$ 的FC-投射分解为 $\dots \to P_{n + 2} \to P_{n + 1} \to G_{n} \to 0$ ，从而得正合列 $0 \to G_{i + 1} \to P_{i + 1} \to G_{i} \to 0$ ，其中 $G_{i}$ 是Gorenstein FC-投射的， $i \geq n$ ，在正合列 $0 \to M \to D \to G^{0} \to 0$ 中， $G^{0}$ 是Gorenstein FC-投射的，所以存在R-模的正合列 $0 \to G^{0} \to P^{1} \to P^{2} \to \dots$ ，其中 $P^{i}$ 是 FC-投射的，令 $G^{i} = I m (P^{i} \to P^{i + 1})$ ，进而有正合列 $0 \to G^{i} \to P^{i + 1} \to G^{i + 1} \to 0$ ， $i \geq 0$ 。从而有正合列

$\dots$

$0 \to G^{1} \to P^{2} \to G^{2} \to 0$

$0 \to G^{0} \to P^{1} \to G^{1} \to 0$

$0 \to M \to D \to G^{0} \to 0$

$0 \to G_{1} \to P_{1} \to M \to 0$

$0 \to G_{2} \to P_{2} \to G_{1} \to 0$

$\dots$

将上述序列作直和得到正合列

$0 \to N \to Q \to N \to 0$ ，

其中 $N = \oplus_{i \geq 1} G_{i} \oplus M \oplus_{i \geq 0} G^{i}$ ， $Q = \oplus_{i \geq 1} P_{i} \oplus D \oplus_{i \geq 1} P^{i}$ ，则M是N的直和项，由( [7] 命题5.5)知， $G F C - p d_{R} (N)$ $= S u p {G F C - p d_{R} (G_{i}), G F C - p d_{R} (G^{i}), G F C - p d_{R} (M) | i \in I} \leq n$ ， $F C - p d_{R} (Q) = S u p {F C - p d_{R} (P_{i}), F C - p d_{R}$ $(P^{i}), F C - p d_{R} (D) | i \in I} \leq n$ ，由引理3.7知，对任意内射维数有限的有限余表现模Q，都有 $E x t_{R}^{n + 1} (N, Q) = 0$ ，因此N是强n-Gorenstein FC-投射模。

( $\Leftarrow$ ) 设N是强n-Gorenstein FC-投射R-模，且 $N = M \oplus Q$ ，由命题3.5可得， $G F C - p d_{R} (N) \leq n$ 。又由( [7] 命题5.5)可得， $G F C - p d_{R} (N) = S u p {G F C - p d_{R} (M), G F C - p d_{R} (Q)}$ ，所以 $G F C - p d_{R} (M) \leq n$ 。

基金项目

国家自然科学基金项目(11361051)。

NOTES

^*第一作者。

^#通讯作者。

参考文献

[1]	Auslander, M. and Bridger, M. (1969) Stable Module Theory. In: Memoirs of the American Mathematical Societyc, Amer. Math. Soc, Providence, RI, Vol. 94. https://doi.org/10.1090/memo/0094
[2]	Enochs, E.E. and Jenda, O.M.G. (1995) Gorenstein Injective and Projective Modules. Mathematische Zeitschrift, 220, 611-633. https://doi.org/10.1007/BF02572634
[3]	Holm, H. (2004) Gorenstein Homological Dimensions. Journal of Pure and Applied Algebra, 189, 167-193. https://doi.org/10.1016/j.jpaa.2003.11.007
[4]	Mahdou, N. and Tamekkante, M. (2009) Strongly n-Gorenstein Projective, Injective and Flat Modules. Proceedings of the American Mathematical Society, 143, 235-251.
[5]	刘仲奎, 刘妍平. 强n-Gorenstein C-投射模和内射模[J]. 西北师范大学学报(自然科学版), 2013, 49(4): 1.
[6]	Gao, Z. and Jenda, H. (2013) On Strongly Gorenstein FP-Injective Modules. Communications in Algebra, 25, 3035-3044. https://doi.org/10.1080/00927872.2012.672601
[7]	Wang, Y. and Zhou, D.X. (2020) Gorenstein FC-Projective Modules. Journal of Algebra and Its Applications, 19, Article ID 2050066. https://doi.org/10.1142/S0219498820500668
[8]	Xue, W.M. (1999) On N-Presented Modulesand Almost Ex-cellent Extensions. Communications in Algebra, 27, 1091-1102. https://doi.org/10.1080/00927879908826483
[9]	王玉, 周德旭. 关于强Gorenstein FC-投射模[J]. 福建师范大学学报(自然科学版), 2018, 34(5): 18-24.
[10]	Huang, Z.Y. (2013) Proper Resolutions and Gorenstein Categories. Journal of Algebra, 393, 142-169. https://doi.org/10.1016/j.jalgebra.2013.07.008
[11]	Enochs, E.E. and Jenda, O.M.G. (2000) Relative Homological Algebra. In: de Gruyter Expositions Mathematics, Vol. 30, Walter de Gruyter, Berlin.

为你推荐

友情链接