Lamb波在抛物线型声黑洞薄板结构中的传播特性

Study the Propagation Characteristics of Lamb Waves on Parabolic Acoustic Black Hole Thin Plate Structures

摘要: 本文利用激光激发的超声Lamb波，对抛物线型声黑洞结构薄板上Lamb波的传播特性及轨迹进行了研究。基于在金属材料中激发超声的热弹机制，建立了激光在抛物线型声黑洞结构薄板上激发Lamb波的三维有限元模型。声波以激发区域为中心向外扩散传播，且大部分的声波能量形成平行于激光线源的波振面，并沿垂直于激光线源方向向外传播。当声波开始进入声黑洞的结构中时，向着厚度减小的方向传播，同时波束宽度会变小，振幅逐渐变大。最后，研究声黑洞底部中心点的位移变化，结果表明峰值位移随着时间稳步上升，具有比较明显的声波聚焦现象。本论文研究成果可用于声黑洞薄板结构的检测与评估。

Abstract: In this paper, the propagation characteristics of Lamb waves on thin plate structure with parabolic acoustic black hole are studied by using laser ultrasonic technology. Based on the thermoelastic mechanism, a three-dimensional finite element model of laser excitation of Lamb wave in thin plate structure with parabolic acoustic black hole is established. Then, the acoustic wave propagates outward as the excitation region is the centre; the wave is parallel to the laser line source; and its propagation direction is perpendicular to the laser line source. When the sound wave encounters the acoustic black hole, it will propagate along the thickness decreasing direction. Meanwhile, the acoustic beam width decreases, and the amplitude gradually increases. Finally, the acoustic amplitude at the lowest point of the acoustic black hole increases gradually, which present the sound wave focusing phenomenon. The results of this paper can be used to detect and evaluate the thin plate structure with acoustic black hole.

1. 引言

Lamb波是平板按自由边界条件解波动方程时得到的一种特殊的波动解 [1]，被广泛应用于两个平行表面结构中的无损检测。利用其能量集中在薄板结构的上、下两个平面内，传播过程中衰减，可以实现非接触式激发，对于大规模薄板结构的无损检测具有极其重要的意义 [2]。

早期，Johnson利用脉冲激光在薄板上激发Lamb波，并用激光干涉仪对波信号进行接收，分析了激光总能量、能量密度及其光斑大小对最低阶模态Lamb波S₀模态和A₀模态的影响 [3]。Charles利用叠加激光线源在薄铝板中激发窄带Lamb波，降低信号的复杂性。从实验和数值模拟两个方面，对S₀模态和A₀模态波在缺陷处的反射系数分析，得到缺陷的尺寸信息 [4]。孙宏祥利用有限元方法研究了激光激发Lamb波在粘弹性薄板中的传播，发现材料的粘弹特性会引起不同模式Lamb波的不同程度的振幅衰减 [5]。许伯强基于有限元法和模态展开法对各向异性板中激光Lamb波的传播特性进行了研究，得到材料的各向异性性质与Lamb波的不同方向的色散特性密切相关 [6]。根据Lamb波在薄板中传播的频散特性，赵振宁采用双重时间尺度对比的方式对超声检测中获取的信号进行分析 [7]。对几何结构不均匀的薄板，弯曲波在其中的传播速度随着厚度变化而改变。当薄板厚度变化满足幂律分布h(r) = εr^m，2 ≤ m，ε为常数时，声波会出现零反射且永远无法达到边界，类似于光黑洞吸收周围光线与能量，这样的结构会吸收周围的声波及能量，因此也被称之为声黑洞 [8]。颜士玲采用全光学激光超声激发与探测系统对Lamb波在含声黑洞结构的薄板中的传播进行了实验研究，实验结果验证了该结构对声波的聚焦作用；同时建立A₀模态Lamb波在声黑洞结构中传播的3D有限元模型，从能量角度计算分析了声黑洞结构对声波的局域作用 [9]。相比于一维声黑洞结构，二维声黑洞结构在实际生活与工业加工中更加实用 [10]。黄薇对二维声黑洞对于弯曲波的能量聚集效应进行过探讨 [11]。

本文对抛物线型声黑洞结构薄板上Lamb波的传播特性及轨迹进行了研究。基于热弹机制，建立激光在抛物线型声黑洞结构上激发Lamb波的三维有限元模型。首先，研究了声波以激发区域为中心向外扩散传播的轨迹；当声波遇到声黑洞时，研究了声波的传播轨迹、振幅变化；最后对声黑洞底部中心点的位移变化进行分析，研究了声波聚焦现象。本论文研究成果可用于声黑洞薄板结构的检测与评估。

2. 理论研究

基于热弹性理论，建立激光线源作用于薄板，激发产生Lamb波的理论模型。考虑到激光作用于薄板的热扩散和声波的传播特性，建立三维模型，其示意图如图1所示。建立厚度变化满足三维抛物线型声黑洞结构的模型，模型主要通过三维参数化曲面与16 × 16 × 0.5 mm的光滑均匀铝制薄板做布尔操作构建而成，模型中抛物线面的开口为一个半径为2 mm的圆，薄板厚度为0.5 mm，抛物线型坑的厚度变化满足z = 0.0625 × (x² + y²)，−2 mm ≤ x ≤ 2 mm，−2 mm ≤ y ≤ 2 mm。

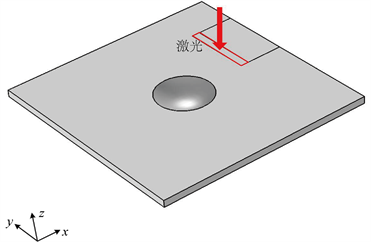
Figure 1. Schematic diagram of laser irradiation two-dimensional parabolic acoustic black hole structures

图1. 激光辐照三维抛物线型声黑洞结构示意图

脉冲激光垂直辐照到薄板表面后，其能量被表层迅速吸收。根据能量守恒的原理，材料表面吸收激光能量后，将引起表层温度的升高及表层局部的体积膨胀，从而产生瞬态位移场 [12]。当薄板厚度与超声波波长具有相同数量级时，在薄板表面生成的横波和纵波耦合形成Lamb波。根据板中质点位移起震的分布方向将Lamb波分为两类模态，对称模态与反对称模态，其传播方向如图2所示。除了拥有多种模态的特点之外，Lamb波主要还存在着频散特性，也因此导致了Lamb波的复杂的传播特性。

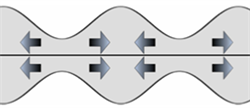(a) 对称模态的Lamb波 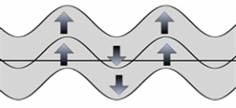(b) 反对称模态的Lamb波

Figure 2. Schematic diagram of symmetry and antisymmetry Lamb wave mode

图2. 对称与反对称模态的Lamb波示意图

在对厚度线性变化的薄板进行研究时，采用脉冲激光线光源。激光作为热通量作用于薄板，非激光辐照区域按绝热条件处理。假设薄板表面存在一个随时间变化的外部热源，激光辐照区的边界条件满足

$-k\frac{\partial T\left(x,y,z,t\right)}{\partial n}=I_{0}A\left(T\right)f\left(x\right)g\left(t\right)$ (1)

其中，A(T)是材料表面的吸收率，I₀是脉冲激光的峰值功率密度，g(t)为时间分布函数，f(x)为激光的空间分布函数，表达式为

$g\left(t\right)=\frac{8t^3}{t_0^4}\exp \left(\frac{-2t^2}{t_0^2}\right)$ (2)

$f\left(x\right)=\frac{1}{\sqrt{2\pi }}\frac{2}{R_G}\exp \left(\frac{-2{\left(x-x_0\right)}^2}{R_G^2}\right)$ (3)

式中，R_G为线源半宽，x₀定义了线光源位置，t₀为激光一个脉冲的宽度。为了避免边界反射对声波传播特性的影响，对模型的四个侧面设置低反射边界条件，其余为自由边界。模型初始温度为室温，初始的位移为零。

Figure 3. The meshing of three-dimensional parabolic acoustic black hole structure

图3. 三维抛物线型声黑洞结构网格划分

为了满足超声波传播精度的要求，对于空间分布为高斯型的脉冲激光，网格单元的最大尺寸选择120 μm，激光辐照区和抛物线底部区域网格划分更密，大小为5 μm，选取自由剖分四面体网格对模型进行划分，如图3所示。时间步长的选择可以决定计算结果中结构响应最高频率和解的精确度，在此时间步长取值为4e−9 s，总计算时间t取值为5 μs。忽略铝材料参数对温度的依赖性，常温下使用的铝板材料的参数如表1所示。

Table 1. Parameters of aluminum

表1. 铝板材料的参数

3. 结果与讨论

根据上文所述理论建立激光线源作用于抛物线型声黑洞薄板结构的模型。激光线源沿z轴负方向垂直作用于模型，确保Lamb波在薄板中的激发与传播。激光线源中心位于x₀ = 2 mm，y方向0 mm~5 mm区域(线源长度约为5 mm)，线源半宽为R_G = 0.15 mm，激光脉冲的上升时间是t₀ = 10 ns，激光脉冲中心辐射能量I₀为 1 × 10¹¹ W/m²。

(a) t = 0 μs (b) t = 0.5 μs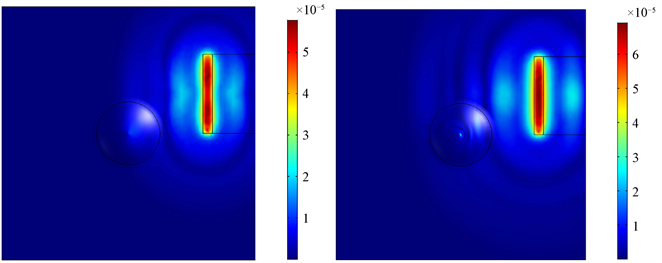(c) t = 1 μs (d) t = 1.5 μs

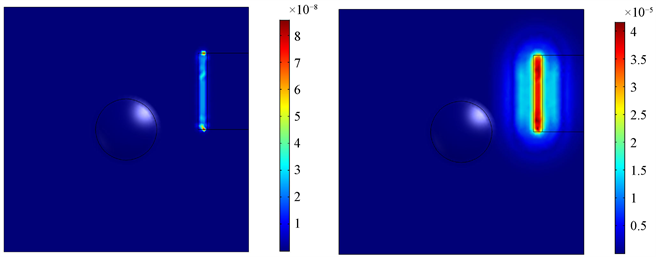
Figure 4. The displacement field of Lamb wave at 0 μs, 0.5 μs, 1 μs, 1.5 μs

图4. 不同时刻(t = 0 μs, 0.5 μs, 1 μs, 1.5 μs)时Lamb波传播的位移场

图4给出了激光激发产生的Lamb波在0.1 μs、0.5 μs、1.0 μs、1.5 μs时刻的位移场分布。其中，颜色代表了位移场大小，红色表示位移场最大，蓝色表示位移场为零。在t = 0 μs，激光作用于如模型所示的长方形区域，激光与薄板进行热交换形成温度梯度，进而形成向外传播的Lamb波。t = 0.5 μs，声波以激发区域为中心向外扩散传播，且大部分的声波能量形成平行于激光线源的波振面，并沿垂直于激光线源方向向外传播。根据所建立的模型得知，抛物线型声黑洞底部中心与线源起点都在y = 0 mm处，因此抛物线型声黑洞位于声波传播的路径上。t = 1.0 μs声波除了沿垂直于线光源位置向外传播，部分声波传播进入声黑洞。t = 1.5 μs，进入声黑洞的声波波振面发生弯曲，向着厚度降低即坑底的方向传播，且声黑洞中心出现应力集中的点。声波在声黑洞结构中究竟是怎么传播的？在此将黑洞结构放大，观察其应力的变化，如图5所示。

(a) t = 2 μs (b) t = 3 μs(c) t = 4 μs (d) t = 5 μs

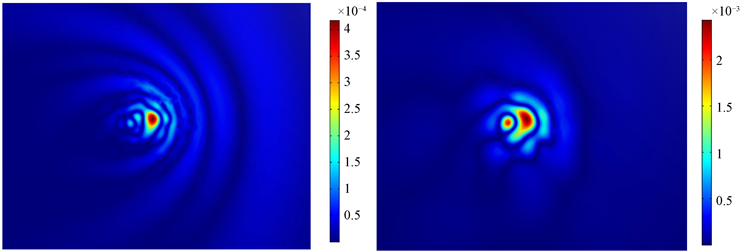
Figure 5. The displacement field of black hole at 2 μs, 3 μs, 4 μs, 5 μs

图5. 不同时刻(t = 2 μs, 3 μs, 4 μs, 5 μs)时声黑洞结构位移场分布

在t = 2 μs，声黑洞底部正中心位置为位移最大点，最大值为4.2 × 10⁻⁴ mm，且声波在声黑洞结构中以底部为中心弯曲传播，越接近底部中心位移越大。Lamb波在厚度减小的薄板中传播时，会向着厚度减小的方向传播，波的波速会随着厚度的减小而减小，波束宽度变小，同时波的振幅会随着厚度的减小而增大。t = 3 μs，底部位移最大值为24 × 10⁻⁴ mm。位移的显著增大表示声波能量的集中，由此可初步看出声波向底部中心汇聚。时间为4 μs，5 μs时，底部中心位移最大值为36 × 10⁻⁴ mm、39 × 10⁻⁴ mm，声波振幅增速变缓。此时，一个激光脉冲激发产生的Lamb波已经传播通过，但是声黑洞中能量集中于底部，具有比较明显的声波聚焦现象，且不会随着声波传播时间变长而减弱。

Figure 6. Schematic diagram of the center of black hole at (0 mm, 0 mm, 0 mm)

图6. 声黑洞底部中心(0 mm, 0 mm, 0 mm)取点示意图

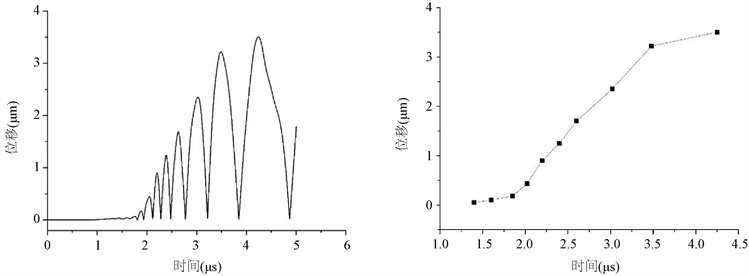
为了进一步的分析声黑洞底部能量的变化，如图6所示取坑底处红色的三维截点，并绘制该点在y方向的位移–时间图，如图7(a)所示。由图中可以看出，在0 μs~1.8 μs时间内，声波未传播到黑洞底部，位移保持为0。时间大于1.8 μs，该点处的位移逐渐变大。由于声波位移是双极性的，该点处的位移起伏变化，且位移的峰值逐渐增大。对此绘制位移峰值点大小随时间变化的曲线，如图7(b)所示。在2.0 μs~3.5 μs时间段位移峰值线性增加，此处为声波传播进入黑洞；在3.5 μs后，位移峰值变化趋缓，表示声波传播基本结束。峰值位移随着时间稳步上升，说明随着时间的推移，声黑洞结构将周围的声波以及声波能量吞噬，该点处的能量越来越大。

(a) (b)

Figure 7. (a) The displacement-time diagram and (b) the change of the peak displacement of the black hole center

图7. (a) 声黑洞底部中心点的位移–时间图，(b) 声黑洞底部中心点位移峰值变化图

4. 总结

本文对抛物线型声黑洞结构薄板上Lamb波的传播特性及轨迹进行了研究。首先，基于在金属激发超声的热弹机制，建立激光在抛物线型声黑洞结构上激发Lamb波的三维有限元模型。激光沿z轴负方向垂直作用于模型薄板区域，确保Lamb波在薄板中的激发与传播。在0 μs~1.5 μs时间内，声波以激发区域为中心向外扩散传播，且大部分的声波能量形成平行于激光线源的波振面，并沿垂直于激光线源方向向外传播。声波传播进入声黑洞，声波波振面发生弯曲，向着厚度降低即坑底的方向传播，并且在声黑洞底部中心集中。1.5 μs~5 μs内，声波继续向着厚度减小的方向传播，波速随着厚度的减小而减小，波束宽度逐渐变小，同时波的振幅会随着厚度的减小而增大。最后，通过分析声黑洞底部中心点的位移变化，发现峰值位移随着时间稳步上升，具有比较明显的声波聚焦现象。本论文研究成果可用于声黑洞薄板结构的检测与评估。

基金项目

国家自然科学基金项目“基于激光超声的楔体缺陷检测与评估方法研究”(11704096)。