1. 引言
转向架作为高速动车组的核心部件,其性能状态直接影响高速动车组运行的安全性。研究表明,在动车组故障诱因中,大约30%是由转向架的损坏引起的。现阶段,国内动车组轴承故障的研究多集中于对轴承的故障诊断研究,且多以专家经验作为诊断依据;对轴承故障的预测性研究略显不足,而对故障的预测性研究是实现动车组轴承的计划性维修向其状态性维修过渡的有效手段。为此,本文在对转向架故障发生特点和状态表征参数进行充分研究的基础上,结合三次指数平滑法的优势,构建了基于三次指数平滑法的转向架关键参数趋势预测模型。本文对CRH380动车组转向架轴承温度与轴箱齿轮温度数据进行了预测,验证了方法的有效性。
2. 国内外现状
目前,关于转向架故障诊断的研究,国内外学术团体及工业界已开展了广泛的工作。杨三叶研究了滚动轴承的故障诊断分类,分析了样本的特性后选用了鲁棒性好的SVM。并且为了提高诊断准确率,选用了全局性能良好的搜索者优化算法(SOA)对SVM的参数进行优化。最终确定了基于SOA的SVM故障诊断算法,并利用仿真数据验证了此算法的可行性 [1]。冯新扬基于深度学习理论,提出了将CNN算法结合Softmax分类器,针对数据集不平衡问题引入加权损失函数和正则化等模型优化技术,搭建适于滚动轴承故障诊断的改进型深度卷积神经网络模型实现了轴承故障信号特征提取与目标分类 [2]。荆云建使用CWRU轴承标准数据集进行建模分析,验证了卷积神经网络从原始一维振动信号逐层卷积池化来抽取故障特征,并实现不同类型,不同程度故障准确分类的算法可行性 [3]。关于基于三次指数平滑法进行时序数据预测的研究也取得了一定成果。王国权等提出了一种自适应的动态三次指数平滑方法来进行风速预测,该方法利用了地毯式搜索方法,根据误差平方和最小的原则及时调整并获得最佳的平滑系数,然后进行后续的一步或多步风速预测 [4]。韩坤提出了基于非线性最小二乘法的指数平滑系数α选取方法,其核心思想在于根据预测值与实测值之间的拟合误差平方和最小值,利用非线性最小二乘法中具有松弛性质的搜索算法,通过高斯–牛顿迭代程序估计最优指数平滑系数α,使得指数平滑预测模型在预测过程中达到更为精准的预测精度 [5]。然而上述研究主要是针对已获取的转向架监测数据进行分析,实现对转向架系统当前运行状态和健康度的评价,对现阶段动车组由计划性维修向状态性维修过渡的目标帮助不够显著,故而实现在基于现有转向架监测数据基础上的预测具有更大的实际意义。
3. 三次指数平滑法
指数平滑法是一种时间序列分析方法,时间序列分析预测方法根据适用性的不同,可以分为全期平均法、移动平均法和指数平滑法等。其中,指数平滑法是通过计算指数的平均值,结合合理的时间序列预测模型,依据当前数据呈现的变化趋势对未来进行预测的方法。三次指数平滑法是指数平滑法中的一种,适用于时间序列呈抛物线变化的非线性数据。
3.1. 基于三次指数平滑法的趋势预测模型
设n个转向架部件检测参数组成的时间序列为
,则转向架关键参数预测模型为:
(1)
其中:
(2)
(3)
(4)
(5)
式中:
为转向架部件监测参数预测值;T为预测超前时间;at,bt,ct为t时刻的预测系数;
为第t时刻对应的三次指数平滑值;α为加权系数,且
;
,
,
分别为一次、二次、三次指数平滑的平滑初始值。
3.2. 模型求解
1) 初始值确定。由于转向架系统各部件在运用过程中积累了丰富的数据,并且动车组具有单次运行时间和旅程长的特点,因此采用三次指数平滑法进行转向架关键部件参数预测时,初始值对预测结果产生的影响较小,因而选择原始数列的第1期的实际数据作为初始值。
2) 加权系数选择。加权系数α是在预测过程中,改变新旧数据对预测影响力的比例因子。α越大,表明新数据对预测结果的影响越大,预测结果的灵敏度越高,对新水平的适应性越好;反之,对实际数据的变化反应迟钝,容易产生滞后性。当机械设备的检测参数一般呈现随时间变化而波动,但长期趋势变化不大的特点时,应选取稍大的α值,一般在0.3~0.5之间取值。当数据长期趋势变化较大,呈现明显且迅速的波动时,应选取较大的α值,一般在0.6~0.8之间取值。
3) 数据预测。
①将初始值与加权系数α代入公式(5)至(7)中,得到更新后的一次、二次、三次指数平滑值;
②根据公式(2)至(4)计算当前和过去时段的转向架关键系统部件监测参数预测系数,为三次指数平滑法计算提供基础;
③根据公式(1),选取适合的预测超前指数,对未来数据进行预测,并得到最终结果。
4. 转向架关键参数趋势预测
4.1. 确定权重系数
以动车组转向架轴承温度监测数据为例,图1表明动车组转向架关键系统部件监测参数呈现随时间变化而波动,但长期趋势变化不大的特点,因而本文选取的α值为0.3~0.5之间,为提高算法的预测性能,采用均方误差最小化的方法来确定α的值,采用的MSE方法如下
其中,n为预测的监测参数的数,Y(t)为预测值,X(t)为检测到的数值。

Figure 1. Trend change of temperature monitoring data of bogie pinion
图1. 转向架小齿轮温度监测数据趋势变化
为使MSE最小化,方法如下:对参数α范围内的所有数从初始值0开始,以一个定步长∆α增长,即α = α + ∆α,直至α = 1结束,对于每一个α值,根据所选的指数平滑模型,计算模型预测值,然后计算该 对应的MSE,最后选取最小的MSE对应的α为最优模型参数。
4.2. 预测结果分析
为了验证基于三次指数平滑法的转向架关键参数趋势预测方法的有效性,本文使用获取的CRH380BL动车组转向架的轴承温度数据和小齿轮温度数据进行了测试,结果如下:
图2为转向架轴箱电机侧的小齿轮温度,其中红色为监测到的齿轮温度实际数据,蓝色为基于三次指数平滑法的预测数据。由图可知,蓝色曲线与红色曲线相比,虽然存在时间上的迟滞现象,但保持了基本一致的变化趋势,特别是在45~75 s,85~95 s之间,现象较为明显。在135~140 s之间,蓝色曲线的变化趋势与红色曲线相比略有不同,说明算法在参数选择上仍有优化的必要性。
图3展示的是转向架驱动电机侧轴箱轴承温度的趋势变化。由图可知,蓝色曲线与红色曲线相比保持了基本一致的变化趋势,特别是在80~95 s处,140~150 s处,蓝色曲线的预测值与红色曲线的实际值偏差趋近于0,表明本文使用的三次指数平滑模型能够有效实现轴箱轴承温度的变化趋势预测。在150 s处,蓝色曲线的最高点比红色曲线相比虽然存在3℃左右的偏差,但仍能够实现轴承温度的有效预测。

Figure 2. Pinion temperature-motor side
图2. 小齿轮温度–电机侧
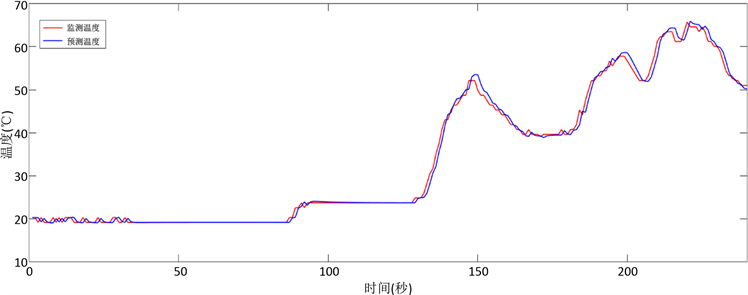
Figure 3. Axle box bearing temperature-drive side
图3. 轴箱轴承温度–驱动侧

Figure 4. Pinion temperature-wheel side
图4. 小齿轮温度–轮侧
图4为转向架轮侧的驱动电机小齿轮温度变化趋势图。由图可知,在140~250 s之间,虽然存在1 s左右的延时,但与红色曲线相比仍保持了基本一致的变化趋势。在150 s处,蓝色曲线的峰值数据与红色曲线相比约有3℃左右的偏差,这与图3相似,证明本方法在对数据快速变化的预测能力上仍有改进空间,但即使是这样的误差,仍不影响对转向架故障的预测。
5. 结论
如何提高动车组运行安全性、可用性及降低运维成本,提高我国高铁动车组健康管理和运维决策水平,已成为轨道交通行业可持续发展的战略问题和迫切需求。转向架作为高速动车组的核心部件,其性能状态直接影响高速动车组运行的安全性。本文提出的基于三次指数平滑法的转向架关键参数趋势预测方法能够有效预测转向架关键部件表征参数变化趋势的方法,对提高转向架运行的安全性及计划修向状态修的过渡有着重要的意义。