基于平面应变模拟特征的钢棒相似土抗剪强度试验研究

Experimental Study on Shear Strength of Analogical Soil Based on Characteristics of Plane Strain Simulation

摘要: 为拓展土工模型试验技术手段，减少试验设备条件限制，本文针对可用于土工模型试验平面应变模拟的钢棒相似土材料，通过设计改造直剪仪开展了不同粒径级配条件下的直剪试验。结果表明，钢棒相似土受剪时类似于密砂，呈明显的应变软化现象，且峰值强度与上覆荷载及粒径级配密切相关，剪切特性符合库仑强度理论。由此，计算得到不同粒径级配工况下的钢棒相似土内摩擦角，建立了平均粒径与内摩擦角的数学关系。研究结论可用于平面应变条件下土工模型试验的设计与计算。

Abstract: In order to expand the technical means of geotechnical model test and reduce the limitation of test equipment, in this paper, the direct shear tests under different particle size gradations of analogical soil materials that can be used for plane strain simulation of geotechnical model test, are carried out by designing and modifying the direct shear apparatus. The results show that the analogical soil is similar to dense sand in shear, showing obvious strain softening phenomenon, the peak strength is closely related to the overlying load and particle size gradation, and the properties of shear conform to Mohr-Coulomb strength theory. Therefore, the internal friction angle of analog cal soil is calculated under different particle size gradations conditions, and the mathematical relationship between average particle size and internal friction angle is established. The research conclusion can be used for the design and calculation of geotechnical model test under plane strain condition.

1. 引言

近些年来，随着国内外工程建造水平的提高，为优化结构受力或满足特殊工程需求，越来越多的新型土工构筑物得以研发及应用。相比较传统结构，这些新型结构受力性能较好，但往往也存在受力机理不明确、设计计算复杂等问题。因此，为了揭示土工构筑物的受力机理及承载特性，构建理论计算方法，土工模型试验被大量应用于理论研究中，如挡土墙、抗滑桩、基坑支护等。为简化边界条件、减少试验干扰因素，土工模型试验大多采用砂土作为填料。然而，由于砂土是一种颗粒材料，其力学行为由颗粒间的相互作用力所决定，并具有不连续、非均质、易压缩、压实度难准确控制等特征，使得土工模型试验测试结果可重复性较差。因此，如何改进试验材料，提高模拟结果的可靠性，成为研究者非常关心的技术问题，并研究提出了相似土技术。该技术最早由Schneebeli (1956) [1] 报道，提出可以由铝、钢、铜、木材等不同材质制成不同重度的相似土材料，并可通过改变截面形状模拟颗粒间的嵌挤状态，通过对棒材料表面进行处理模拟颗粒间的摩擦性能，证明了可以通过棒状材料模拟符合Mohr-Coulomb强度准则的二维均匀颗粒介质。

因此，基于相似土技术具有的重度可调、无压缩性、材料均匀性好、可重复性强、符合平面应变假定等特征，目前在土工模型试验中得到了较多的应用 [2]。如Ladanyi (1969) [3] 通过采用Schneebeli棒材料模拟颗粒土体，开展了在理想平面应变条件下的多组活动门试验，监测了活动门上的土压力变化，并用相机拍摄了棒状材料的运动轨迹。芮瑞等人(2017) [4]、Bhandari和Han (2018) [5] 采用该类相似材料，研究了桩承式路堤的土拱效应及变形特性。而Ugai和Desai (1995) [6]、Huang (2009, 2010) [7] [8]、Colas等人(2009) [9] 利用Schneebeli材料作为填料，分别针对加筋土挡墙、悬臂式挡墙等支挡结构开展了模型试验，研究了其受力及变形特性。

尽管如此，目前相似土材料在国内土工试验中的应用较为少见，其中最大困难在于基本参数的测定。相似土材料抗剪强度的测定大多采用双轴压缩试验，该设备价格高、数量少，使得该材料的应用受到了很大限制 [9] [10]。为推动相似土材料在土工模型试验中的应用，Colas等人(2009) [9]、Jenck等人(2009) [10] 通过采用直剪试验和双轴试验的对比，验证了采用直剪试验进行抗剪强度指标测定的可靠性。

因此，为了准确获得相似土材料的力学参数并降低相似土土工试验的成本，本文改造了现有土体抗剪强度测试装置，使其能更广泛地用于相似土土工试验。通过直剪试验得到了钢棒相似土材料的剪应力–位移曲线，进而分析不同粒径下相似土的力学参数，研究成果可为相关土工模型试验研究提供测试数据。

2. 相似土剪切试验

2.1. 试验装置

因基于平面应变特征的相似土均为等长的圆棒或椭圆棒，逐根排列后呈立方体形状。同时，金属相似土为憎水性材料，不需要进行饱水处理。因此，为模拟钢棒相似材料的剪切特性，本文将常规土工直剪仪的上、下剪切盒改造为10 cm × 10 cm × 10 cm的方形结构，采用应变控制进行直剪试验。

2.2. 试验材料

本试验所用相似土为圆形钢棒，直径分别为3 mm、4 mm、5 mm，长度为10 cm，如图1所示。钢棒相似土的几何与物理参数见表1所示。

Figure 1. Steel bars with different diameters

图1. 不同直径钢棒

Table 1. Geometric and physical parameters of analogical soil

表1. 钢棒相似土几何与物理参数

2.3. 试验步骤

1) 按照不同级配下钢棒体积比换算为质量，称取相应质量钢棒，并进行均匀混合；

2) 安装上下剪切盒，调好位置，将称取好的钢棒均匀放入剪切盒内；

3) 调整平衡杠杆(杠杆比为1:12)和加压架，推动剪切盒使其与测力计接触，调整测力计百分表读数为零。开动剪力机，使其与下剪切盒接触后停止。试验中垂直应力分别为50 kPa、100 kPa、150 kPa、200 kPa，通过相应重量的砝码施加。垂直荷载施加后，便开始剪切试验。

4) 开动剪力机，快剪试验以1.2 mm/min的剪切速率快速进行，每转一圈0.2 mm剪切位移记录一次测力计读数，当钢环测力计百分表指针不前进并开始后退时，表示试样已经破坏，之后记录10圈即停止剪切；

5) 改变钢棒级配，重复1)~4)步骤，相应得到不同级配下的钢棒相似土抗剪强度参数。

2.4. 试验工况

为了研究不同级配下的钢棒相似土抗剪强度，设计了5种不同试验工况，如表2所示。

Table 2. Geometric and physical parameters of analogical soil

表2. 钢棒相似土几何与物理参数

注：V₃:V₄:V₅分别代表钢棒直径为3 mm、4 mm、5 mm的体积。

排列完成后的钢棒如图2所示。

(a) 单粒径排列 (b) 混合粒径排列

Figure 2. Arrangement of steel bars under different gradation conditions

图2. 不同级配条件下的钢棒排列方式

3. 试验结果分析

3.1. 钢棒相似土剪切应力–位移曲线

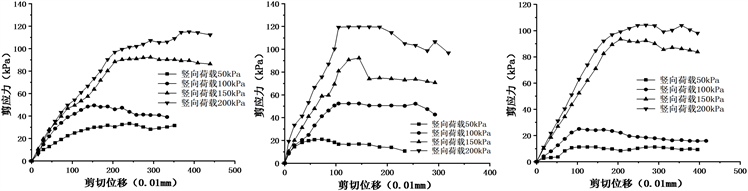
不同粒径条件下的钢棒相似土直剪试验结果如图3、图4所示，由图可知，无论对于单粒径还是混合粒径，随着剪切位移的增加，试样剪应力均增大，至峰值后呈现一定的应变软化现象，达到残余状态。同时，随着竖向压力的增加，峰值应力明显提高，且达到峰值应力的位移量也明显增大，表明钢棒相似土类似于密砂，这种强度的减小是因为剪切位移克服了钢棒之间的咬合作用后，钢棒结构体发生滚动卸荷的结果。

其中，图3为单一粒径(D分别为3 mm、4 mm、5 mm)钢棒剪切应力-位移曲线。由图可知，在竖向压力较低时( ${\sigma }_c\le 100\text{kPa}$ )，粒径越大，峰值应力水平越低，达到峰值状态的剪切位移越小。如竖向压力为100 kPa时，D = 3 mm、4 mm、5 mm对应的峰值应力分别为52.4 kPa、53.2 kPa、26.8 kPa，对应位移分别为1.47 mm、1.15 mm、1.08 mm。钢棒粒径对峰值应力水平影响与越大，峰值应力越低。但当竖向压力为150 kPa、200 kPa时，则粒径对钢棒相似土峰值应力的影响减弱。另外，由该图还可发现，在竖向压力分别为150 kPa、200 kPa时，相似土粒径越大，剪切模量越高，但在低竖向压力状态下则差别不大。

(a) D = 3 mm (b) D = 4 mm (c) D = 5 mm

Figure 3. Shear stress-displacement curve of analogical soil under single particle size

图3. 单一粒径时钢棒相似土剪切应力-位移曲线

图4为混合粒径混合工况4、5的剪切应力–位移曲线。相比较单粒径工况，等体积混合条件下的钢棒相似土剪应力峰值与单粒径相接近，而等数量混合条件下的钢棒相似土剪应力峰值则明显偏低。同时，混合粒径组合条件下剪应力峰值对应的应变量明显增大，表明此条件下的相似土剪切模量发生降低。分析原因，因三种粒径差别较小，进行混合粒径组合时，其堆积密度变小，使得受剪时要发挥同样的剪切强度，所需位移量更大。相比较同体积混合与等数量混合条件，尽管前者的密度小于后者，但前者所含的3 mm粒径的钢棒数量明显多于后者，使得前者剪应力峰值明显高于后者，表明在混合粒径混合条件下，小粒径钢棒的比例对抗剪强度的发挥起主要控制作用。因此，对于钢棒相似土，当采用单粒径进行试验时，钢棒的粒径越大，对应的密度和抗剪强度越大；但当采用混合粒径组合时，小粒径钢棒的比例越大，抗剪强度较高，但对应的密度降低。

(a) 体积比1:1:1 (b) 体积比9:16:25

Figure 4. Shear stress-displacement curve of analogical soil under mixed particle size

图4. 混合粒径时钢棒相似土剪切应力–位移曲线

3.2. 钢棒相似土内摩擦角

3.2.1. 单粒径

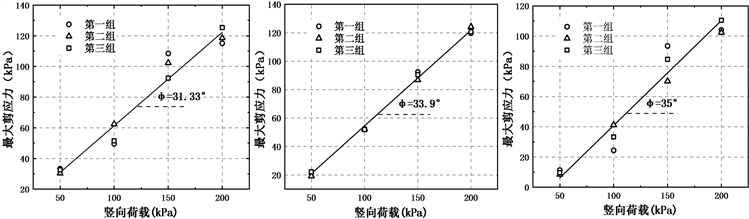
图5为单粒径条件下钢棒相似土 ${\tau }_f-p$ 曲线。综合三组平行试验的结果可以看出，不同粒径下的钢棒相似土均呈现出随着竖向荷载的增加，最大剪应力线性增大的趋势。这说明钢棒相似土材料符合摩尔–库伦材料的特点。排除试验测试误差，钢棒相似土 ${\tau }_f-p$ 曲线为近似通过坐标原点的直线，符合无粘性土特性。因此，由无粘性土抗剪强度计算公式 [11] $\tau =\sigma \times \tan \phi$，可计算得到不同粒径条件的钢棒相似土内摩擦角，如D分别为3 mm、4 mm和5 mm时，内摩擦角分别为31.33˚、33.9˚及35˚。

(a) D = 3 mm (b) D = 4 mm (c) D = 5 mm

Figure 5. Steel bars with single particle size

图5. 单粒径钢棒

3.2.2. 混合粒径

图6为混合粒径条件下钢棒相似土 ${\tau }_f-p$ 曲线，由图可知，在不同粒径混合比下，钢棒相似土的直剪试验仍表现出随着竖向荷载的增加，峰值剪应力线性增大的趋势。 ${\tau }_f-p$ 曲线特征与单粒径工况相同，符合摩尔–库伦材料中无粘性土特征。由图可得，体积比1:1:1试样的内摩擦角 $\phi$ 为33.7˚，体积比9:16:25试样的内摩擦角 $\phi$ 为21.8˚。

(a) 体积比1:1:1 (b) 体积比9:16:25

Figure 6. Analogical soil of steel bars with mixed particle size

图6. 混合粒径钢棒相似土

根据以上试验数据，汇总得到不同粒径级配下钢棒相似土的内摩擦角，如表3所示。

Table 3. The internal friction angle of analogical soil under different grades (c = 0)

表3. 不同级配下钢棒相似土的内摩擦角(c = 0)

表4为土壤内摩擦角参考值 [12]，对照表3中结果可知，前四种工况主要集中于中砂–粗砂范围，而第五种工况则差别较大，这与剪切盒尺寸偏小有较大关系，测得试验误差偏大。

Table 4. Reference value of soil internal friction angle [12]

表4. 土壤内摩擦角参考值 [12]

为便于试验应用，进一步分析钢棒平均粒径与内摩擦角的关系，整理绘制图7所示，并拟合得到二者关系如式(1)所示。由图可见，在一定范围内相似土的内摩擦角随着钢棒平均粒径的增加而增大。采用式(1)所示的抛物线函数可以比较好的模拟钢棒相似土平均粒径与内摩擦角之间的关系。

$\phi =-0.635{\bar{d}}^2+6.915\bar{d}+16.3$ (1)

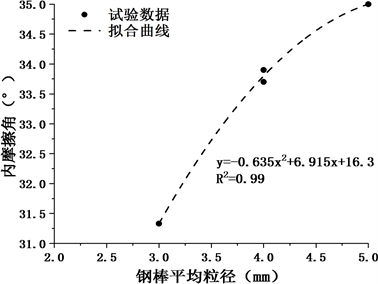
Figure 7. The relationship of the average particle size and the internal friction angle

图7. 钢棒平均粒径与内摩擦角关系图

4. 钢棒相似土抗剪强度形成机理

库仑抗剪强度公式 [11] $\tau =c+\sigma \tan \phi$ 表明，土的抗剪强度由两部分组成，即摩擦强度 $\sigma \tan \phi$ 和黏聚强度c。通常认为，粗粒土颗粒间没黏聚强度，即 $c=0$。

摩擦强度决定于剪切面上的正应力 $\sigma$ 和土的内摩擦角 $\phi$。钢棒相似土的内摩擦涉及钢棒之间的相对滑动，其物理过程包括如下两个组成部分：一是钢棒之间滑动时产生的滑动摩擦；二是钢棒之间由于咬合所产生的咬合摩擦。

滑动摩擦是由于钢棒接触面粗糙不平引起的，钢棒之间的滑动摩擦可用滑动摩擦角 ${\phi }_u$ 表示，钢–钢的摩擦系数一般为0.12~0.15，换算为滑动摩擦角为6.8˚~8.5˚。

咬合摩擦是指相邻钢棒对于相对移动的约束作用。如图8(a)所示，为相互咬合排列的钢棒。当钢棒内沿某一剪切面产生剪切破坏时，相互咬合着的钢棒必须从原来的位置被抬起(如图8(b)中的颗粒A)，跨越相邻颗粒(颗粒B)，然后才能移动。总之，先要破坏原来的咬合状态，一般表现为体积胀大，即所谓“剪胀”现象，才能达到剪切破坏。剪胀需要消耗部分能量，这部分能量需要由剪应力做功来补偿，即表现为内摩擦角的增大。钢棒粒径越小，排列越密，咬合作用越强，则内摩擦角越大。

(a) 受剪前 (b) 受剪后

Figure 8. Shear mechanism diagram of analogical soil

图8. 钢棒相似土受剪机理图

5. 结论

本文针对可用于土工模型试验平面应变模拟的钢棒相似土材料，为替代复杂且试验费用高的双轴压缩试验，改造了传统的直剪盒并开展了基于直剪试验的研究。测得了不同单粒径及不同粒径混合比下的剪应力–位移曲线，进而获得了不同粒径级配下钢棒相似土内摩擦角，并从剪切角度分析了钢棒相似土的强度机理，得到了如下结论：

1) 通过改造常用直剪盒，可用于模拟钢棒相似土的直剪试验，为土工模型试验的开展积累了经验，提供了一种新试验途径。

2) 钢棒相似土受剪时呈现明显的应变软化现象，且峰值强度与上覆荷载及粒径级配密切相关。

3) 钢棒相似土剪应力–竖向压力关系线表明，其剪切特征类似于无粘性土，符合库仑强度理论，抗剪强度可由内摩擦角及竖向压力的变化予以反映。

4) 根据不同粒径级配工况下的钢棒相似土内摩擦角，建立了平均粒径与内摩擦角的数学关系。