复杂环境下大型挠性航天器的振动抑制与能量采集

Vibration Suppression and Energy Harvesting of Large Flexible Spacecraft under Complex Environments

摘要: 该研究提出使用非线性能量阱(Nonlinear Energy Sink, NES)对复杂环境下的大型挠性航天器进行振动抑制，并利用超磁致材料(Giant Magnetostrictive Materials, GMM)采集NES耗散的振动能，达到节约能源的效果。考虑太阳光压和热冲击的影响，建立Hamilton体系下大型挠性航天器的在轨动力学模型。根据Newton动力学定律得到NES的振动抑制方程，引入Jiles-Atherton模型求得GMM的能量采集表达式。将NES-GMM耦合于航天器的两自由端，利用Galerkin法对整体结构进行离散化，采用Runge-Kutta法进行数值仿真。结果表明NES对航天器的振动抑制效果十分显著，同时GMM能够采集NES耗散的部分振动能，因此该方案是完全可行的，此外适当调整NES和GMM的结构参数还可以提高工作性能。该研究为振动控制与能量采集技术在航天领域的应用提供了新的思路。

Abstract: This study proposed Nonlinear Energy Sink (NES) for the vibration suppression of large flexible spacecraft in complex environments, and Giant Magnetostrictive Materials (GMM) for harvesting the vibrational energy dissipated by NES to reach the effect of energy saving. Considering the influence of sunlight pressure and thermal shock, the in-orbit dynamic model of large flexible spacecraft was established in the Hamilton system. The NES equations of vibration suppression were obtained according to Newton’s dynamic laws, and introducing Jiles-Atherton model deduced the GMM expressions of energy harvesting. NES-GMMs were coupled to the both free ends of spacecraft, which was discretized by Galerkin method, and Runge-Kutta method was used for numerical simulations. The results demonstrated that the effect of NES on the vibration suppression of spacecraft is greatly significant. Meanwhile, GMM can harvest parts of the energy dissipated by NES. Therefore, the proposed method is completely feasible. Moreover, properly adjusting the structural parameters of NES and GMM can also improve the working performance. This study provides a new idea for the application of the technologies of vibration control and energy harvesting in the aerospace field.

1. 引言

近年来随着航天事业的飞速发展，各类航天器所承担的任务也越来越复杂，故需要航天器具有更强的功能性，比如空间太阳能电站需要提供更多的能源，完成更高效的发电；空间机器人需要具备更大的活动范围和更灵活的工作方式等，这些需求都促使航天器向大型化发展 [1] [2]。此外为降低发射成本，提高工作效率，低刚度材料逐渐用于大型航天器的设计与制造，因此大型挠性结构在航天领域中得到了非常广泛的应用。

然而大型挠性航天器在轨运行时会受到各种空间干扰的作用，如太阳光压力矩、热冲击、重力梯度力矩等，由于自身大尺寸、高柔度的特性，航天器的内部结构极易产生剧烈振动，因此很多学者针对航天器的结构振动问题展开研究。Malla讨论了航天器简化模型的不同方案，并进行了相应的动力学分析，研究结果发现在大姿态角的条件下，姿态运动和结构振动会对航天器的动力学行为产生很大影响 [3]。李学府建立了绳系空间太阳能电站的动力学模型，研究了太阳能电站的非线性动力学行为，利用数值仿真得到其动力学响应，结果表明横向振动对太阳能电站的影响远大于轴向振动 [4]。McNally进一步研究了柔性哑铃模型的热环境-结构振动耦合动力学问题，仿真结果表明热环境的变化和温度场的非均匀分布能够导致结构的弯曲变形，同时也会影响自身的姿态运动 [5]。

大型挠性航天器的结构振动会使系统产生极大的不稳定性，严重影响正常的在轨运行，因此对航天器进行高效的振动控制是十分必要的，这引发了许多学者的研究与讨论。Sabatini将基于绳索的太阳能电站的功率传输面板简化为欧拉梁，使用推进器和压电装置对太阳能电池板进行振动控制，数值仿真验证了该方案的可行性，并发现面板刚度会对控制效果产生影响 [6]。张天丽提出了一种基于超磁致伸缩致动器的位移定位与控制系统，并对该系统的动力学模型及控制方法进行了描述，结果表明阶跃响应下的超磁致伸缩致动器具有良好的位移定位和控制性能 [7]。然而以上两种控制器都需要大量的外部能源作为输入，且控制效果均有待提高。陈阳在不改变航天器现有结构的条件下，设计了新型圆盘隔振器来实现整星隔振，结果表明该隔振器用于航天器的振动抑制是可行的，此外航天器-隔振器系统的振动传递率和阻尼比会影响其抑制性能 [8]。

伴随着整星隔振技术的迅速发展，非线性能量阱(Nonlinear Energy Sink, NES)应运而生，NES由粘弹性阻尼、质量块和非线性刚度弹簧组成，设计良好的NES可以提供强大的振动抑制能力，其耗散的能量也可被回收和再利用 [9]。孔宪仁研究了NES的能量靶向传递现象，利用复平均法求解出系统能量与各参数的近似关系，给出了NES具备抑制能力时线性阻尼的有效范围，数值仿真验证了上述结果 [10]。臧健开始将NES应用到整星系统中，通过Runge-Kutta法分析了NES对系统响应的抑制效果，结果表明NES能够实现对整星系统的振动抑制 [11]，然而将NES用于大型挠性航天器的振动抑制还有待研究。与此同时，超磁致材料(Giant Magnetostrictive Materials, GMM)凭借能量密度高、响应快和寿命长的优势，可显著提高振动能的采集效率。贾振元考虑了GMM的非线性问题，建立了基于磁感应强度的GMM动力学模型，并进行了仿真分析，结果表明增大磁感应强度可提高GMM的能量采集效率 [12]。孟爱华设计了一种柱棒式GMM振动能量采集器，对GMM的物理特性进行分析，完成了GMM装置的建模、仿真和实验，结果说明了该装置具有良好的能量采集性能 [13]。然而GMM在航天领域的应用仍处于起步阶段，需要进一步研究和讨论。

针对上述问题，本文提出一种将NES与GMM同时用于大型挠性航天器的新方案。在太阳光压和热冲击作用下，建立由大型挠性航天器和NES-GMM组成的振动抑制与能量采集系统。数值仿真验证了该方案的可行性，还分别研究了NES和GMM的结构参数对自身工作性能的影响。该方案既保证了航天器在复杂环境中的稳定运行，又实现了能源的节约，为提高振动抑制与能量采集效率也提供了一些参考。

2. 大型挠性航天器在轨动力学建模

基于Hamilton原理，对复杂空间环境下的大型挠性航天器进行在轨动力学建模，首先做出如下假设：

(1) 在本文中，地球被视为一个理想球体。

(2) 航天器以特定的轨道绕地球运行。

(3) 航天器的长度远大于厚度。

(4) 忽略航天器的扭转和剪切变形。

因此，可以将航天器简化为两端自由、只进行轴向运动的Euler-Bernoulli梁平面模型。结合小变形假设，只考虑航天器垂直于正表面方向的振动 [14]。取航天器几何中心的运动作为整体的轨道运动，图1给出了大型挠性航天器的在轨运行简图。其中， $O_e$ 代表地心； $O_e{x}_0{y}_0$ ， $O_e{x}_e{y}_e$ 分别代表轨道和惯性坐标系； $R_1$ 为轨道半径； $\phi$ 为航天器的面上姿态角； $\theta$ 为轨道倾角； $F$ 代表航天器所受的空间干扰合力；航天器位于xy平面内，其几何中心O作为浮动坐标系的原点，x轴与y轴分别沿航天器的切线和法线方向。在浮动坐标系上航天器发生弯曲变形， ${\rho }_P$ 代表航天器变形前P点相对于O点的位置矢量 $OP$ ； $w_P$ 代表航天器变形前后P点的横向变形矢量。因此，P点相对于地心 $O_e$ 的位置矢量 $r_P$ 可以表示为：

$r_P=A_e^o{R}_1+A_e^o{A}_o^a\left({\rho }_P+w_P\right)$ (1)

式中， $A_e^o$ 表示轨道坐标系到惯性坐标系的变换矩阵，而 $A_o^a$ 表示浮动坐标系到轨道坐标系的变换矩阵，二者可以由式(2)分别表示：

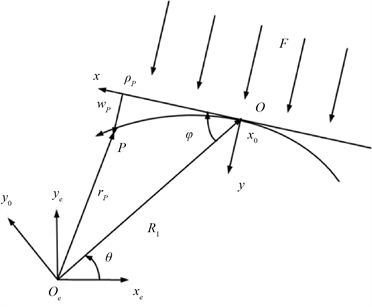
Figure 1. Schematic diagram of large flexible spacecraft in orbit

图1. 大型挠性航天器在轨运行简图

$A_e^o=\left[\begin{array}{ccc}\cos \theta & 0& \sin \theta \\ 0& 1& 0\\ -\sin \theta & 0& \cos \theta \end{array}\right]$, $A_o^a=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \phi & -\sin \phi \\ 0& \sin \phi & \cos \phi \end{array}\right]$ (2)

随后，开始计算航天器在轨运行时产生的动能和势能。设航天器上P点的线密度为 $m_P$ ，则P点的动能可以表示为：

$T_P=\frac{1}{2}{m}_P\frac{\text{d}{r}_P^{\text{T}}}{\text{d}t}\cdot \frac{\text{d}{r}_P}{\text{d}t}$ (3)

对式(3)关于时间进行积分，可以得到航天器整体的动能表达式为：

$\begin{array}{l}T=\frac{1}{2}{\displaystyle \int \{{\left(\frac{\partial w}{\partial t}\right)}^2}+{\left({\omega }_0{R}_1\right)}^2+\left(w^2+x^2\right){\left({\omega }_0+\frac{\text{d}\phi }{\text{d}t}\right)}^2+2{\omega }_0{R}_1\frac{\partial w}{\partial t}\cos \phi \\ +\left[2{\omega }_0{R}_1\left(x\cos \phi -w\sin \phi \right)+2x\frac{\partial w}{\partial t}\right]\left({\omega }_0+\frac{\text{d}\phi }{\text{d}t}\right)\}\text{d}{m}_1\end{array}$ (4)

式中， $m_1$ 代表航天器质量。航天器的总势能由应变能和重力势能两部分组成。其中，航天器的应变能只包括弯曲变形能，且由于航天器低轨运行，其重力可近似等于万有引力。二者表达式分别为：

$U_d=\frac{1}{2}{\displaystyle \int EI}{\left(\frac{{\partial }^{2}w}{\partial x^2}\right)}^2\text{d}x$, $U_g=-{\displaystyle \int \frac{\mu }{r}\text{d}{m}_1}$ (5)

式中， $\mu$ 为地球引力常数， $\mu =G{m}_1$ ，G为万有引力常量， $G=6.67\times {10}^{-11}\text{N}\cdot {\text{m}}^2/{\text{kg}}^2$ ；r为航天器上某一点到地心 $O_e$ 的距离，其表达式为：

$r=\sqrt{R_1{}^2+x^2+w^2+2x{R}_1\cos \phi -2w{R}_1\sin \phi }$ (6)

在空间环境中，太阳光压和热冲击会对航天器的在轨运行产生极大影响。太阳光压是由太阳辐射与航天器表面的相互作用产生的一种空间摄动力，当航天器运动到阴影区域时，太阳光压将会消失。施加在航天器正表面的太阳光压及力矩可分别表示为：

$F_s={\displaystyle {\oint }_A\text{d}{f}_s}$, $T_s={\displaystyle {\oint }_A{r}_s\times \text{d}{f}_s}$ (7)

式中， $\text{d}{f}_s$ 表示作用在航天器表面面元 $\text{d}A$ 上的太阳光压，其表达式为 [15]：

$\text{d}{f}_s=\left(\frac{2}{3}{C}_{rd}+2C_{rs}\cos \beta \right)n{\rho }_s\text{d}A+p_{1}H\left(\cos \beta \right)\cos \beta \left(a_s+C_{rd}\right)r_s$ (8)

式中， $p_1$ 为太阳辐射常数； $n$ 为面元 $\text{d}A$ 的法向量； $a_s$ 为太阳光的吸收率，则反射率 ${\rho }_s=1-a_s$ ； $C_{rd}$ 为漫反射比，设 $K_s$ 为漫反射系数，则有 $C_{rd}=K_s{\rho }_s$ ； $C_{rs}$ 为镜面反射比， $C_{rs}=\left(1-K_s\right){\rho }_s$ ； $\beta$ 为太阳光的入射角， $\beta =0$ 为太阳光压的最大值点。故结合式(7)~(8)，太阳光压对航天器做的功可由下式计算：

$W_s={\displaystyle {\int }_0^{\frac{\pi }{2}}{T}_s}\text{d}\phi$, $\beta =0$ (9)

此外，航天器从阴影区运行至光照区时，会突然受到强高温作用，即热冲击现象。已知航天器的长厚比极大，故其正表面的温度场可视为仅关于y坐标的函数。在受热均匀的条件下，航天器的传热过程只发生在沿y轴方向。设航天器正表面的材料参数与温度无关，由Fourier定律可得到温度场的动态方程为 [16]：

$k_t\frac{{\partial }^{2}T}{\partial z^2}+\delta q_t=\rho c_t\frac{\partial T}{\partial t}$ (10)

式中， $k_t$ 、 $\rho$ 和 $c_t$ 分别代表航天器的导热系数、面密度与比热容； $q_t$ 为热冲击载荷， $\delta$ 为 $q_t$ 的相对参数，当热冲击作用于航天器的正表面时， $\delta =1$ 。下面引入热力学第一定律 [17]：

$Q=c_t{m}_1\Delta T={\alpha }_{t}S{H}_{t}t$ (11)

式中， $\Delta T$ 为航天器受到热冲击前后的温度差； ${\alpha }_t$ 为航天器正表面的热吸收率； $H_t$ 为太阳辐射热流。假定航天器不与外界环境发生热交换，则热冲击对航天器做的功可由下式计算：

$W_t={\displaystyle {\int }_0^L{\displaystyle {\int }_0^{h}E{\alpha }_t}}{\alpha }_e\frac{S{H}_t}{c_t{m}_1}y\text{d}y\frac{\partial y}{\partial x}\text{d}x$ (12)

式中，h、E和 ${\alpha }_e$ 分别表示航天器的厚度、弹性模量与热膨胀系数。已知航天器的总动能、势能与合外力功，故引入Hamilton方程：

${\displaystyle {\int }_{t_1}^{t_2}\left(\delta T-\delta U+\delta W\right)\text{d}t=0}$ (13)

因此将式(4)、(5)、(9)和(12)代入式(13)，经整合可得到大型挠性航天器的在轨动力学方程组，如下所示：

${\displaystyle \int [\frac{{\text{d}}^2\phi }{\text{d}{t}^2}}\left(x^2+w^2\right)+2w\left({\omega }_0+\frac{\text{d}\phi }{\text{d}t}\right)\frac{\partial w}{\partial t}+\left(W_s+W_t\right)+\left({\omega }_0^2-\frac{\mu }{r^3}\right)R_1\left(x\sin \phi +w\cos \phi \right)+x\frac{{\partial }^{2}w}{\partial t^2}]\text{d}x=0$ (14)

$\frac{{\partial }^{2}w}{\partial t^2}+\left[\frac{\mu }{r^3}-{\left({\omega }_0+\frac{\text{d}\phi }{\text{d}t}\right)}^2\right]w+x\frac{{\text{d}}^2\phi }{\text{d}{t}^2}+\left(W_s+W_t\right)+\frac{EI}{\rho A}\cdot \frac{{\partial }^{4}w}{\partial t^4}+\left({\omega }_0^2-\frac{\mu }{r^3}\right)R_1\sin \phi =0$ (15)

式(14)中，第1、2项代表航天器的姿态运动与结构振动的耦合项；第4项中的 $-\mu /r^3$ 为重力梯度项；第5项为振动加速度项。而式(15)中，第2项表示航天器的重力梯度与姿态-振动的耦合项；第3项表示姿态角的加速度项；第5项中的 $EI/\rho A$ 表示航天器正表面的弯曲强度。

3. NES振动抑制与GMM能量采集

随着振动控制技术的不断创新，出现一类由弹簧、阻尼与小型质量块组成的振动抑制装置，根据弹簧的线性和非线性，装置可分为两类：线性吸振器和NES，相比于线性吸振器，NES具有工作效率高、吸振频带宽和鲁棒性强等优势，故可将NES用于航天器的振动抑制，NES的结构如图2所示。

Figure 2. Diagram of NES structure

图2. NES结构示意图

其中，m代表NES的质量；c代表NES的阻尼；k代表NES的非线性弹簧刚度。根据Newton第二定律，NES的动力学方程如下：

$m\ddot{z}+c\left(\stackrel{\dot{}}{z}-\stackrel{\dot{}}{w}\right)+k{\left(z-w\right)}^3=0$ (16)

根据Newton第三定律，可分别得到NES对航天器的控制力及做功表达式：

$F_{NES}=c\left(\stackrel{\dot{}}{w}-\stackrel{\dot{}}{z}\right)+k{\left(w-z\right)}^3$, $W_{NES}={\displaystyle {\int }_0^L{F}_{NES}w\text{d}x}$ (17)

对于线性吸振器，控制系统整体能量表达式为：

$E_{lin}=\frac{{\stackrel{\dot{}}{w}}^2}{2}+\epsilon \frac{{\stackrel{\dot{}}{z}}^2}{2}+\frac{w^2}{2}+k_L\frac{{\left(w-z\right)}^2}{2}$ (18)

式中， $\epsilon$ 为系统参数， $0<\epsilon <1$ ； $k_L$ 表示线性弹簧的刚度。相比于线性吸振器，NES具有更良好的吸振机理-靶向能量传递(Targeted Energy Transfer, TET)：当NES耦合至航天器主体时，系统产生的振动能传递给NES。随着振动能不断被NES耗散，整个振动系统进入共振状态。直到某一时刻，能量传递结束，NES可耗散系统中的大部分能量。基于线性控制系统(18)，航天器-NES系统的整体能量可以表示为：

$E_{NES}=\frac{{\stackrel{\dot{}}{w}}^2}{2}+\epsilon \frac{{\stackrel{\dot{}}{z}}^2}{2}+\frac{w^2}{2}+\epsilon k\frac{{\left(w-z\right)}^4}{4}$ (19)

此外，得益于TET机理，NES耗散的振动能也可以进行回收和再利用。因此，本文引入GMM能量采集技术，在NES进行振动抑制的同时，采集其耗散的部分振动能，最终达到节约能源的效果。图3给出了GMM能量采集装置的截面图。

图中，阴影区域代表附有感应线圈的GMM棒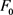； $F_{GMM}$ 、分别表示GMM棒所受的压力和装置内部产生的预紧力。基于Villari效应 [18]，可得GMM的本构方程如下：

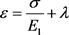(20)

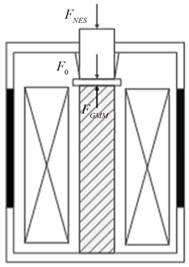
Figure 3. Sectional diagram of GMM energy harvester

图3. GMM能量采集装置截面图

(21)

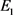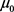式中，、和分别代表GMM棒的应变、压应力和弹性模量；B、和分别为GMM棒的磁场强度、压磁系数和磁导率；H、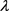分别为GMM的外加偏置磁场和磁致伸缩系数，其中的表达式为：

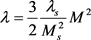(22)

式中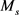，、和M分别表示GMM的饱和磁致伸缩系数、饱和磁化强度和总磁化强度。由应变的定义可知：

(23)

式中，、u和分别为GMM棒的长度、初始位移和预应力引起的位移。下面给出Jiles-Atherton模型的表达式：

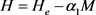(24)

(25)

(26)

(27)

(28)

式中，、和分别表示GMM的有效磁场强度、无磁滞磁化强度和畴壁作用系数；a、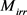和分别为无磁滞形状系数、不可逆磁化强度与不可逆损耗系数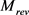；、和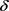分别为可逆磁化强度、比例系数和符号函数，其中。引入机电耦合模型 [19]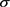，与M的关系式为：

(29)

式中，代表GMM棒的能量耦合系数。在进行振动控制之前，GMM内部无预应力和磁场，因此设初始条件为、，则有：

(30)

结合式(23)，根据Faraday电磁感应定律可知，磁通量的变化能够产生感应电动势，故GMM装置产生的感应电动势及功率为：

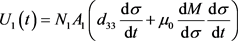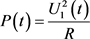, (31)

式中，、和R分别为GMM装置的感应线圈匝数、横截面积和外接电阻。将NES-GMM耦合到大型挠性航天器的两个自由端，如图4所示。

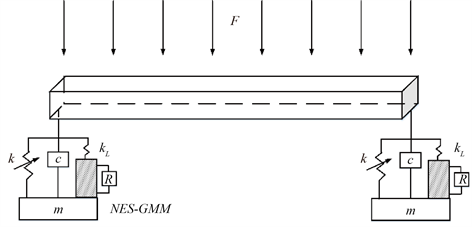
Figure 4. Schematic diagram of large flexible spacecraft in orbit

图4. 大型挠性航天器-NES-GMM示意图

假设用、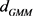分别代表GMM棒所受的预应力与棒体直径，则NES的控制方程为：

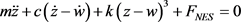(32)

(33)

将式(32)~(33)代入式(14)~(15)，并引入Galerkin法进行离散化，在任意时刻航天器的振动位移都可以表示为：

(34)

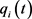式中：为第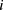阶模态坐标下的位移；表示固有振型函数。由于航天器为轴向运动、两端自由的梁模型，故其边界条件为：

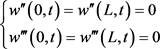(35)

振型函数必须满足上述的边界条件，由式(34)~(35)可求得的表达式如下：

(36)

式中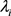，可近似为常数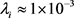，；L为航天器的总长度；的前四个根分别为1.875、4.694、7.855和10.996，且恒成立。经整合，最终得到大型挠性航天器的振动抑制与能量采集方程为：

(37)

(38)

(39)

4. 数值仿真

为进一步验证NES和GMM对复杂环境下大型挠性航天器的振动抑制与能量采集效果，本节采用了计算精度高、效率快的高阶Rungle-Kutta法进行数值仿真，此外还分析了NES的阻尼比和非线性刚度对抑制效果的影响，以及GMM的磁导率和磁致伸缩系数对能量采集效果的影响。已知NES与GMM的相互作用非常弱 [20]，可进行独立讨论。首先表1给出了大型挠性航天器的结构与空间参数，而NES-GMM的结构参数如表2所示。

Table 1. Structural and spatial parameters of large flexible spacecraft [21] [22]

表1. 大型挠性航天器结构与空间参数 [21] [22]

Table 2. Structural parameters of NES-GMM [20] [23]

表2. NES-GMM结构参数 [20] [23]

图5体现了NES对大型挠性航天器的振动抑制效果，首先设NES的初始阻尼比为0.2，非线性刚度为2.5 × 10⁵ N/m。在太阳光压和热冲击的共同作用下，航天器在100 s内一直保持剧烈振动，最大振动位移为2.5 m。加入NES后航天器的振动位移迅速减小，其最大偏差(首个波峰值)降至1.5 m，并最终收敛于t = 75 s处。结果表明在TET过程中NES可以吸收航天器的大部分振动能，因此NES对航天器的振动抑制效果十分显著，能大幅削弱太阳光压和热冲击对航天器的影响。

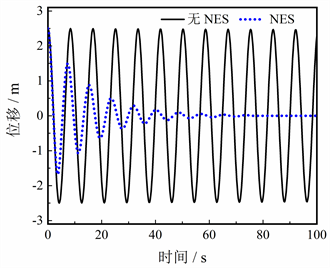
Figure 5. Effect of NES on the vibration suppression of large flexible spacecraft

图5. NES对大型挠性航天器的振动抑制效果

图6说明了NES的阻尼比会影响自身的振动抑制性能，遵循控制变量的原则，取NES的非线性刚度为定值(k = 2.5 × 10⁵ N/m)。当阻尼比c = 0.4时，航天器的振动位移相比于图5 (c = 0.2)明显下降更快，最大偏差减小为0.9 m，最终收敛于t = 40 s处，NES的抑制性能大幅提升。随着阻尼比翻倍(c = 0.8)，最大偏差又降至0.3 m，收敛时间仅为20 s，NES的性能再次提升，这说明NES的阻尼比与TET效率成正相关。因此为了对航天器进行更有效的振动抑制，提高NES的阻尼比是完全可行的，在本文中c = 0.8使NES的性能达到最佳。

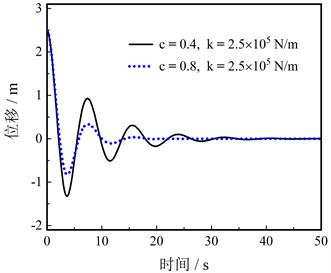
Figure 6. Effect of damping ratio of NES on the performance of vibration suppression

图6. NES的阻尼比对振动抑制性能的影响

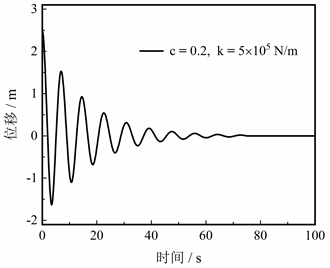
图7评估了NES的非线性刚度对自身抑制性能的影响，同样取NES的阻尼比为定值(c = 0.2)。当非线性刚度k = 5 × 10⁵ N/m时，航天器振动位移的变化与图5基本相同，最大偏差仅增加0.02 m，仍在t = 75 s处收敛(图7(a))。当刚度翻倍后(k = 1 × 10⁶ N/m)，最大偏差又略微增加0.03 m，但收敛时间仍保持不变(图7(b))，这说明NES的非线性刚度对TET进程的作用非常小。因此NES的抑制性能基本不受非线性刚度的影响，k的最优值为5 × 10⁵ N/m。

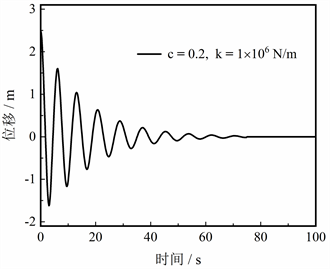(a) (b)

Figure 7. Effect of nonlinear stiffness of NES on the performance of vibration suppression: (a) k = 5 × 10⁵, (b) k = 1 × 10⁶

图7. NES的非线性刚度对振动抑制性能的影响：(a) k = 5 × 10⁵，(b) k = 1 × 10⁶

图8对比了NES的能量耗散和GMM的能量采集情况。根据表2，取GMM的磁致伸缩系数和磁导率的初始值均为2 × 10⁻⁶。在NES的抑制作用下，大型挠性航天器被耗散的振动能大幅增长，前40 s内的增速极高，此后能量增长逐渐平缓，在t = 75 s处达到最大值(9557 J)，这也与图5中NES的控制时间相适应。与此同时GMM采集的振动能总量也在逐渐增加，相比于NES的能量耗散，GMM采集的能量增幅较小，结果表明整个能量采集过程可持续22 s，采集的总能量为1163 J，经计算GMM可采集NES耗散能量的12.17%。因此本文提出的方案是可行的，但仍需进一步增强GMM的采集性能。

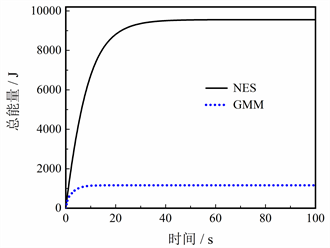
Figure 8. Comparison of NES-GMM on the energy dissipating and harvesting

图8. NES-GMM的能量耗散与采集对比

图9体现了GMM的磁致伸缩系数对能量采集性能的影响，首先设定磁导率的值为2 × 10⁻⁶ N/A²。当磁致伸缩系数λ = 4 × 10⁻⁶时，GMM的能量采集过程可持续30 s，采集的振动能总量为1791 J，是初始值的1.54倍，达到NES耗散能量的18.74%。当λ = 6 × 10⁻⁶时，能量增长十分明显且采集的持续时间延长至75 s，这与NES的能量耗散过程相适应，极大实现了能源节约，此时GMM采集的总能量可达7373 J，是初始值的4.12倍，占NES耗散能量的77.15%。因此为了提升GMM的采集性能，增大λ是非常可行的，λ越接近饱和磁致伸缩系数，GMM性能的提升越显著。

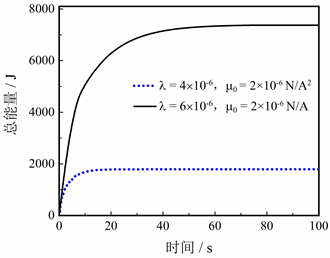
Figure 9. Effect of magnetostrictive coefficient of GMM on the performance of energy harvesting

图9. GMM的磁致伸缩系数对能量采集性能的影响

图10评估了GMM的磁导率对能量采集性能的影响，同样先取磁致伸缩系数为定值(λ = 2 × 10⁻⁶)。当磁导率μ₀ = 4 × 10⁶ N/A²时，GMM采集的振动能总量为1275 J，达到NES耗散能量的13.34%，能量采集过程可持续25 s，与初始值相比有小幅提升。随着μ₀增至6 × 10⁶ N/A²，GMM最多可采集振动能1409 J，占NES耗散能量的14.74%，能量采集过程可延长至30 s，采集效果再次得到提升，结果表明提高GMM的磁导率可进一步增强自身的能量采集性能。因此根据图9~10的仿真结果，GMM的磁致伸缩系数和磁导率均可作为评估其能量采集性能的参数，而进行横向对比时会发现增大磁致伸缩系数对自身性能的提升更显著。

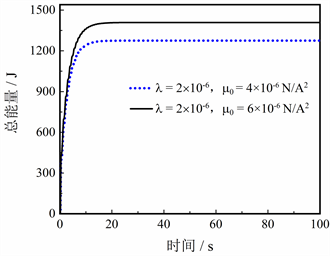
Figure 10. Effect of permeability of GMM on the performance of energy harvesting

图10. GMM的磁导率对能量采集性能的影响

5. 结论

考虑到太阳光压和热冲击的影响，本文建立了大型挠性航天器的在轨动力学模型，利用NES和GMM对航天器分别进行振动抑制和能量采集，数值仿真验证了该方案的可行性，并得到以下结论：

(1) 利用NES对大型挠性航天器进行振动抑制是非常可行的。提高NES的阻尼比会显著增强自身的抑制性能，最快可在20 s内完成航天器的振动抑制，相比之下NES的非线性刚度对其抑制性能无明显影响，结果体现了NES高效、稳定的特性。

(2) GMM能量采集技术用于大型挠性航天器同样是可行的。GMM具有良好的采集性能，其性能与磁致伸缩系数和磁导率均呈正相关，经对比，磁致伸缩系数对于GMM性能的提升更显著，优化后GMM采集的振动能总量占NES耗散的77%以上，采集时间可延长至75 s。

本文同时实现了复杂环境下大型挠性航天器的稳定运行和能源节约，为振动控制与能量采集技术在航天领域的应用提供了新的参考。在此研究的基础上，本文也对下一步的科研工作进行了展望：

(1) 大型挠性航天器的一个重要特点是模态密集，由于结构复杂，模型的准确性也难以保证，对多个模态进行控制时独立模态空间的控制效果可能不佳，而对整个系统进行控制器设计的难度也较大。因此需要进一步结合分布式控制方法，进一步研究结构振动控制方法。

(2) 由于大型挠性航天器的控制性能指标大大提高，系统对控制精度和稳定度的要求也逐渐提高，这些系统特性对大型航天器的控制系统设计提出了严峻挑战。因此需要基于航天器的振动控制，在大挠性结构中加入嵌入式作动器，进一步研究系统布局优化、执行机构配置与布局优化等问题。

致谢

本文作者感谢来自辽宁省教育厅青年基金(JYT19033)和沈阳航空航天大学科研基金(18YB47)的大力资助。