型钢混凝土空间边节点受力性能与抗剪强度研究

Mechanism Performance and Shear Strength Study of SRC Spatial Exterior Joints

摘要: 基于已有试验建立型钢混凝土(SRC)梁柱平面节点有限元模型，在验证数值模拟准确性的基础上，建立SRC空间边节点有限元模型，分析空间加载角度和轴压比对该节点受力性能的影响。通过细化加载角度找出空间边节点柱端峰值荷载与加载角度关系的数学模型。将空间边节点分解为主轴方向的十字形和T形构件进行受力分析，提出空间边节点核心区受剪承载力计算公式，并利用数值模拟结果验证其准确性。研究结果表明：SRC空间边节点在两主轴方向水平荷载作用下的柱端极限承载力不相等，且正向加载下柱端极限承载力高于负向加载；柱端极限承载力与加载角度关系曲线为不对称的椭圆形，可利用椭圆形参数公式分段表示；节点在斜向荷载作用下，核心区抗剪承载力与柱端极限荷载成正比，椭圆形参数公式同样适用于核心区抗剪承载力；SRC空间边节点核心区在斜向加载下的抗剪承载力公式计算值与模拟值吻合良好。

Abstract: A finite element model is presented to analyze the mechanical behavior of steel reinforced concrete (SRC) beam-column plane joints. On the basis of verifying the accuracy of numerical simulation, finite element models of SRC spatial exterior joints were established, and the influence of space loading angle and axial compression ratio on the mechanism performance of the joint was analyzed. The mathematical model of the relationship between the peak load and the load angle was found by refining the loading angle. The spatial exterior joint was decomposed into the cross-shaped and T shaped members in the main axis direction for force analysis, the calculation formula of the spatial joint core area shear capacity is proposed and its accuracy is verified with the numerical simulation results. The research results show that the peak load of the column end loaded along the two main axis directions is not equal, and the ultimate bearing capacity of the column end under positive loading is higher than that under negative loading; the relationship between the ultimate bearing capacity and the loading angle is asymmetric ellipse, and it can be expressed in sections by the ellipse parameter formula; the shear capacity of the joint core area under oblique loading is proportional to the ultimate load of the column end, and the formula is also applicable to the core area shear resistance bearing capacity; the calculated value of core area shear bearing capacity formula under oblique loading is in good agreement with the simulated value.

1. 引言

型钢混凝土结构(Steel Reinforced Concrete Structure，简称SRC结构)是指在混凝土中配置型钢并配有一定受力及构造钢筋的结构 [1]，通过钢与混凝土协同工作，具有承载力高、截面尺寸小、抗震性能好和施工方便等优点，在我国得到日益广泛的应用 [2]。

梁柱节点作为框架结构的传力枢纽，往往受到柱端和梁端共同传来的轴力、剪力和弯矩的作用，受力形式复杂。目前有关型钢混凝土框架节点的试验和理论研究主要集中在平面节点，即节点梁肢柱肢以及荷载和约束均在同一平面内，研究表明型钢混凝土平面节点抗震性能良好，承载能力、延性以及耗能能力均优于普通钢筋混凝土平面节点 [3] [4] [5] [6]。框架结构节点在实际受力过程中，通常承受空间斜向荷载作用，因此学者们开始对空间节点的力学性能进行研究，例如：樊健生等通过方钢管混凝土柱–组合梁空间节点的抗震性能试验，研究加载路径对空间组合节点抗震性能的影响 [7]；王妮等对反复荷载下型钢混凝土异形柱空间角节点的破坏机理及损伤进行了试验研究与理论分析 [8]；陈宗平等对型钢混凝土异形柱–钢梁空间节点进行低周反复荷载试验，分析不同因素对该类节点抗震性能的影响 [9]。

已有的参考文献对于空间节点的研究大多集中于普通混凝土节点以及中间层中节点，对于型钢混凝土空间边节点的研究甚少，本文将对SRC框架结构空间边节点进行受力性能分析与抗剪强度研究：建立型钢混凝土空间边节点有限元模型，分析SRC空间边节点在不同加载角度和轴压比下的受力性能，寻找柱端极限承载力与加载角度的关系，建立斜向加载下空间边节点核心区受剪承载力计算公式并验证其有效性。

2. 平面节点有限元模型建立与有效性验证

2.1. 构造方案

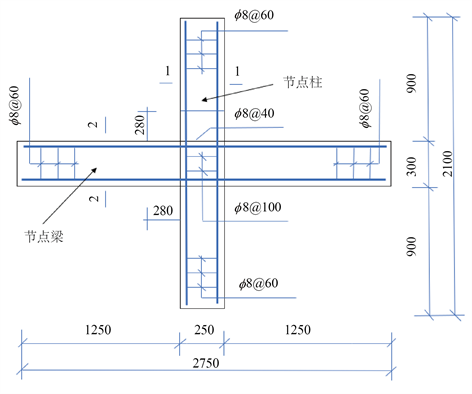
利用ABAQUS进行有限元计算分析，模型选取文献 [10] 中的节点试件。纵筋采用直径20 mm的HRB400级钢筋，箍筋采用直径6 mm的HPB300级钢筋，箍筋间距为加密区40 mm、非加密区60 mm和节点核心区100 mm，混凝土强度等级C50，保护层厚度20 mm，试验轴压比为0.40，型钢截面尺寸 $h_w\times b_f\times t_f\times t_w=130\times 60\times 6\times 8$，试件尺寸如图1所示。

(a) 平面节点 (b) 柱截面 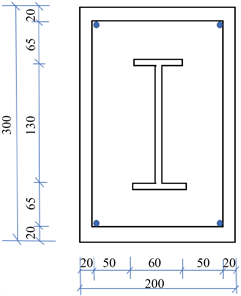(c) 梁截面

Figure 1. Reinforcement arrangement and section shape of specimens (unit of length: mm)

图1. 试件截面形状及配筋(长度单位：mm)

2.2. 本构模型和边界条件

纵筋和箍筋采用钢材的双折线形本构模型，型钢采用三折线形本构模型。混凝土选用塑性损伤本构模型(CDP模型)，该模型可以准确模拟往复荷载下混凝土的受力情况，需要确定混凝土的屈服条件、真实应力–非弹性应变关系、损伤因子。

1) 屈服条件：膨胀角取30度，塑性流动势偏移值取0.1，双轴极限抗压强度与单轴极限抗压强度的比值取1.16，拉压子午面上第二不变量取2/3，粘性系数取0.005 [11]。本文认为混凝土由压转变为拉时无刚度恢复，即取受拉刚度恢复系数 ${\omega }_t=0$，在试算的基础上，取受压刚度恢复系数 ${\omega }_c=0.5$。

2) 应力–应变关系：应力–应变关系按GB50010-2010《混凝土结构设计规范》 [12] 的规定选取，输入ABAQUS时转化为真实应力–非弹性应变关系曲线。

3) 模型通过引入损伤因子d，模拟混凝土在往复荷载作用下的刚度退化，受压和受拉损伤因子 $d_c,d_t$ 均采用文献 [13] 中的表达式。

混凝土和型钢采用实体单元C3D8R，钢筋采用T3D2单元，型钢、钢筋与混凝土之间的相互作用设置为内置区域，混凝土与垫板之间设置为绑定(tie)。

通过设置2个分析步施加边界条件和荷载，第一步施加柱顶轴力，第二步施加柱顶水平位移。

2.3. 验证本文平面节点有限元计算模型可靠性

将本文计算所得SRC平面节点的荷载–位移滞回曲线与试验 [10] 结果进行对比，如图2所示。由图可知，两者前期刚度、峰值荷载以及峰值荷载对应的位移基本一致，表明计算结果与试验结果吻合较好。模拟中的不理想之处表现为滞回曲线的捏拢程度较差，是由于模型中型钢和混凝土之间接触设置为内置区域，不能很好地反映试验中它们之间的粘结滑移。

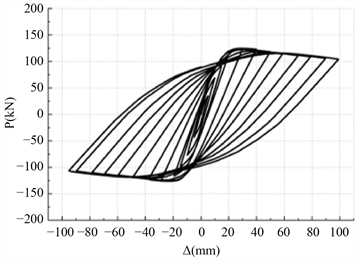(a) 模拟滞回曲线 (b) 试验滞回曲线 [10]

Figure 2. Finite element analysis hysteresis curve

图2. 模拟与试验滞回曲线 [10] 对比

3. SRC空间边节点受力性能

在验证了本文有限元模型准确性的基础上，以空间边节点为研究对象，分析不同轴压比和空间加载角度对空间边节点受力性能的影响。

3.1. 有限元模型

加载角 $\alpha$ 为水平面内加载方向与Y轴的夹角，如图3所示， $\alpha$ 取为0˚，30˚，45˚，60˚和90˚，轴压比为0.3、0.4和0.5。设计参数见表1，图4(a)表示模型概况以及加载局部坐标系的建立，图4(b)表示型钢骨架的受力状态，在往复荷载作用下核心区最大主应力沿对角线斜向分布，符合实际受力状态。

Table 1. Design parameters

表1. 设计参数

(a) 空间受力图 (b) 俯视图

Figure 3. Schematic diagram of load angles

图3. 加载角度示意图

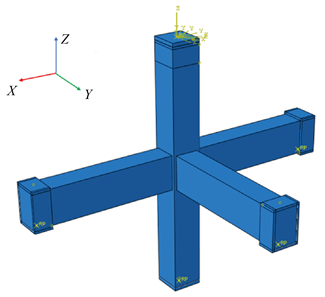(a) 有限元模型 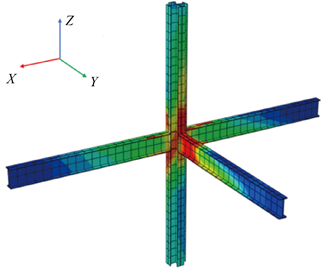(b) 型钢受力状态

Figure 4. Schematic diagram of load angles

图4. 空间边节点有限元模型

3.2. 受力性能

1) 滞回曲线

有限元计算所得各加载工况下节点滞回曲线如图5所示。由图可知，0˚加载角下节点滞回曲线最为饱满，峰值荷载最低，随着加载角度的增加，滞回曲线包围面积减小，峰值荷载相应提高，90˚时节点峰值荷载最大。同时斜向加载时，例如SJ3，负向加载峰值点后强度退化加快，甚至出现结构失稳导致计

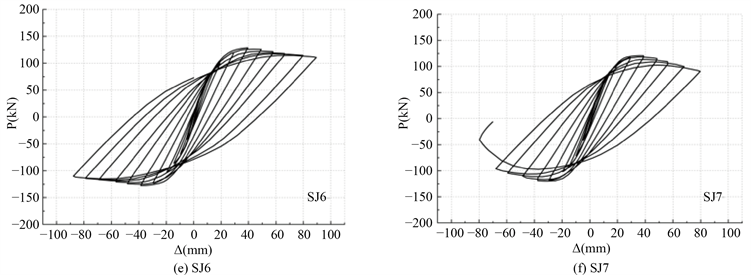
Figure 5. Hysteresis curve of spatial marginal joints

图5. 空间边节点滞回曲线

算不收敛的情况，原因是空间边节点沿Y轴只在单侧有梁，柱顶施加沿Y轴负向的位移时，在轴压力下节点缺乏有效支撑。在不同轴压比下，高轴压比会使峰值点后强度退化加快，负向加载下强度退化速度更快。

2) 骨架曲线

节点荷载–位移骨架曲线如图6所示。在图6(a)中，加载角为0˚节点的峰值荷载比90˚节点的峰值荷载小，这是因为0˚加载方向(Y轴平面内)节点为T形构件，而90˚加载方向(X轴平面内)节点为十字形构件，前者整体刚度较小，且在加载方向节点核心区仅为单侧梁约束，峰值荷载随着加载角度的增加而增大。在图6(b)中，随着轴压比的增大，节点峰值荷载减小，峰值荷载对应的位移相应减小，且峰值点后强度退化速度加快。

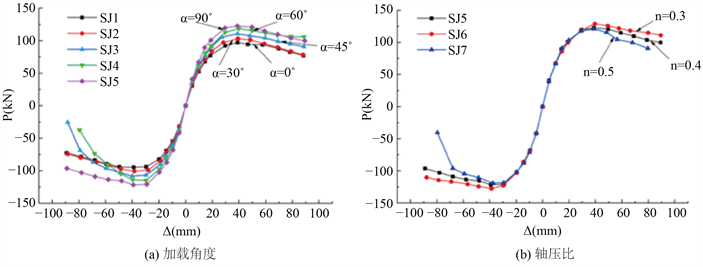
Figure 6. Load-displacement curves under different loading angles and axial compression ratios

图6. 不同加载角和轴压比下节点荷载–位移曲线

4. SRC空间边节点柱端峰值荷载与加载角度关系

4.1. 细化模型参数

为了获取加载角度对节点柱端峰值荷载的影响规律，通过细化加载角度从而建立更多的样本数量以便实现研究目的。型钢混凝土空间边节点关于Y向主轴对称，所以加载角度 $\alpha$ 可定在0˚~90˚之间， $\alpha$ 取为0˚、10˚、20˚、30˚、40˚、45˚、50˚、60˚、70˚、80˚、90˚，对不同加载角度下的计算工况重新编号，分别为GK-1~GK-11。

表2列出了节点柱端沿加载角度方向的峰值荷载，为了直观地描述两者之间的关系，将数据描述在极坐标系中，如图7所示。峰值荷载与加载角度关系曲线近似呈正反向不对称的“椭圆形”，即峰值荷载在0˚加载方向上最小，而在90˚加载方向上最大，且正向加载下节点柱端峰值荷载高于负向加载。

Table 2. Effect of loading angle on the peak load of SRC spatial exterior joints (Unit: kN)

表2. 加载角度对型钢混凝土空间边节点柱端峰值荷载的影响(单位：kN)

注：P_ua表示正向加载下的柱端峰值荷载，P_ub表示负向加载下的柱端峰值荷载。

4.2. 关系曲线数学模型

本文得出柱端峰值荷载与加载角度关系曲线近似为椭圆形，为了找出该曲线数学表达式，参考椭圆

曲线在笛卡尔坐标系下的表达式： $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$，将极坐标系下的参数进行转化。其中极轴a为90˚加载角

下的峰值荷载，极轴b为0˚加载角下的峰值荷载，本文加载角度是指加载方向与Y轴的夹角，因此按 $x=\rho \sin \theta ,y=\rho \cos \theta$ 进行转换，得到以下公式：

正向加载： ${\left(\frac{P_{ua}\sin \theta }{P_{ua,x}}\right)}^2+{\left(\frac{P_{ua}\cos \theta }{P_{ua,y}}\right)}^2=1$ (1)

负向加载： ${\left(\frac{P_{ub}\sin \theta }{P_{ub,x}}\right)}^2+{\left(\frac{P_{ub}\cos \theta }{P_{ub,y}}\right)}^2=1$ (2)

式中， $P_{ua,x},P_{ua,y}$ 分别表示正向加载两主轴方向柱端峰值荷载； $P_{ub,x},P_{ub,y}$ 分别表示负向加载两主轴方向柱端峰值荷载。

图7. 柱端峰值荷载与加载方向关系曲线

5. SRC框架空间边节点核心区抗剪承载力计算

5.1. 节点域受力分析

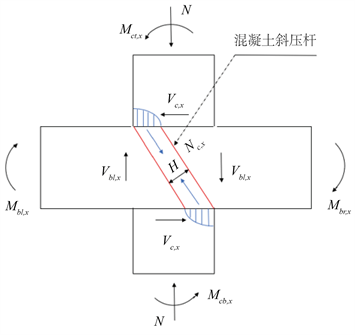
在斜向地震作用下，节点核心区承受来自上下柱，前后左右梁端轴力、弯矩和剪力共同作用。鉴于直接研究空间节点核心区受力机理比较复杂，本文根据已有平面节点受力机理研究成果，将SRC空间边节点沿两主轴方向进行分解，X方向平面内为十字形构件，Y方向平面内为T形构件，主轴方向平面受力简图如图8所示。

由水平方向上力的平衡，X方向的节点核心区水平剪力 $V_{j,x}$ 为 [14]：

$V_{j,x}=T_{r,x}+C_{l,x}-V_{c,x}$， $T_{r,x}=\frac{M_{br,x}}{h_{bw}}$， $C_{l,x}=\frac{M_{bl,x}}{h_{bw}}$ (3)

由于柱反弯点处弯矩为0，因此节点核心区上、下柱根的弯矩：

$M_{cu,x}=V_{c,x}{h}_1$， $M_{cd,x}=V_{c,x}{h}_2$ (4)

(a) X方向 (b) Y方向

Figure 8. Plane force diagram of spindle direction

图8. 主轴方向平面受力简图

由弯矩平衡：

$M_{cu,x}+M_{cd,x}=M_{bl,x}+M_{br,x}$ (5)

由式(4)和式(5)可得：

$V_{c,x}=\frac{M_{cu,x}+M_{cd,x}}{h_1+h_2}=\frac{M_{bl,x}+M_{br,x}}{h-h_b}$ (6)

将式(6)代入式(3)：

$V_{j,x}=\frac{M_{br,x}+M_{bl,x}}{h_{bw}}\left(1-\frac{h_{bw}}{h-h_b}\right)$ (7)

式中， $T_{r,x},C_{l,x}$ 表示梁中传来的拉力和压力； $V_{c,x}$ 为柱端水平剪力；h为柱上下反弯点之间的距离； $h_b$ 为梁截面高度； $h_{bw}$ 为梁端截面拉、压合力点之间的距离，本文通过计算取为240 mm。 $M_{cu,x},M_{cd,x}$ 和 $M_{bl,x},M_{br,x}$ 分别为柱端和梁端的弯矩； $h_1$ 和 $h_2$ 分别为下、上柱反弯点到核心区的高度 [14]。

同理，Y方向的节点核心区剪力 $V_{j,y}$ 可表示为：

$V_{j,y}=\frac{M_{b,y}}{h_{bw}}\left(1-\frac{h_{bw}}{h-h_b}\right)$ (8)

式中， $M_{b,y}$ 为梁根部弯矩。

由式(7)和式(8)可知 $V_{j,x}$ 和 $V_{j,y}$ 均与各主轴方向的柱端水平剪力成正比，因此空间斜向加载下核心区极限水平剪力 $V_j$ 也与柱端斜向荷载 $V_c$ 成正比，有限元模拟计算结果见表3。

Table 3. Test values of ultimate horizontal sheer force in the joint core (Unit: kN)

表3. 节点核心区极限水平剪力数值模拟值(单位：kN)

5.2. 沿主轴方向节点核心区抗剪承载力计算

型钢混凝土节点核心区某一主轴抗剪承载力主要由三部分组成 [14]：1) 混凝土抗剪承载力 $V_c$ ；2) 箍筋抗剪承载力 $V_{sv}$ ；3) 型钢腹板抗剪承载力 $V_{sw}$。

$V_j=V_c+V_{sv}+V_{sw}$ (9)

1) 箍筋

参考钢筋混凝土节点箍筋抗剪承载力 [12]，表达式为：

$V_{sv}=f_{yv}\frac{A_{sv}}{s}\left(h_0-{a^{\prime }}_s\right)$ (10)

式中， $A_{sv}$ 为同一截面箍筋总截面面积； $f_{yv}$ 为箍筋抗拉强度；s为节点核心区箍筋间距； $h_0$ 为柱截面有效高度； ${a^{\prime }}_s$ 为受压钢筋/型钢合力作用点至受压侧边缘的距离。

2) 型钢腹板抗剪承载力

柱弯矩主要由翼缘承担，腹板承担剪力和压力，在屈服前处于弹性阶段，所以节点区腹板抗剪承载力 $V_{sw}$ 为 [14]：

$V_{sw}=\frac{f_{sw}{h}_w{t}_w}{\sqrt{3}}$ (11)

式中， $f_{sw},h_w,t_w$ 分别为型钢腹板的屈服强度、高度及厚度。

3) 核心区混凝土抗剪承载力

混凝土在节点抗剪中占主要地位，极限状态下发生斜压杆破坏，受力模式如图9(a)、图9(b)所示。节点核心区混凝土抗剪承载力取决于混凝土斜压杆的抗压强度和宽度，并且应考虑正交梁的约束对其提高作用。直交梁对节点的约束作用与直交梁的刚度和直交梁截面在节点核心区的面积覆盖率 $\omega$ 有关，西安建筑科技大学根据国内外的试验资料，得出直交梁约束影响系数 $\psi$ 与 $\omega$ 关系如下 [15]：

$\psi =\{\begin{array}{ll}1+1.7\left(\omega -0.25\right)\hfill & \omega \ge 0.25\hfill \\ 1\hfill & \omega \le 0.25\hfill \end{array}$ (12)

$\omega =\frac{A}{h_c{h}_b}$ (13)

式中，A为直交梁的截面面积， $h_c$ 和 $h_b$ 分别为柱截面高度和梁截面高度。

混凝土的抗剪承载力 $V_c$ ：

$V_c=\psi H{b}_j{f}_c\cos \theta$ (14)

式中，H为混凝土斜压杆等效宽度，由 $H=0.5h_c/\sin \theta$ 可得； $b_j$ 为柱有效宽度，取梁柱截面宽度的平均值； $\theta$ 为斜压杆与水平方向的夹角，与构件尺寸和轴压比有关； $f_c$ 为混凝土轴心抗压强度。

将 $H=0.5h_c/\sin \theta$ 代入式(14)可得：

$V_c=\psi 0.5h_c{b}_j{f}_c/\tan \theta$ (15)

(a) X方向 (b) Y方向

Figure 9. Mechanical model of concrete compressive strut in X-Y plane of spatial exterior joint core

图9. 空间边节点核心区主轴方向混凝土斜压杆受力模型

令 $\gamma =0.5/\tan \theta$， $\gamma$ 为综合反映轴压比、混凝土开裂后软化、型钢翼缘和箍筋约束混凝土等因素对节点核心区混凝土抗剪承载力的影响 [15]，则：

$V_c=\gamma \psi h_c{b}_j{f}_c$ (16)

本文通过继续扩大参数寻找 $\gamma$ 与n的关系，分别施加轴压比为0.3、0.4、0.5和0.7的轴压力，沿主轴方向施加水平位移，分别得出不同轴压比下SRC空间边节点沿X和Y主轴方向的柱端峰值荷载，通过式(7)计算出节点核心区主轴方向抗剪承载力 $V_j$，通过下式可以得到不同轴压比n下 $\gamma$ 的值：

$\gamma =\frac{V_j-V_{sw}-V_{sv}}{\psi f_c{b}_j{h}_j}$ (17)

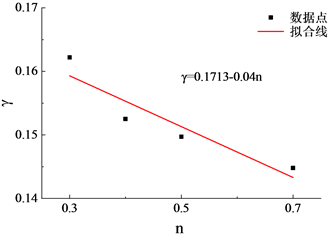
表4给出了不同轴压比n对应的 $\gamma$ 值，对其进行线性拟合，如图10所示。

Table 4. Corresponding value between γ and n

表4. $\gamma$ 与n对应值

(a) X主轴方向 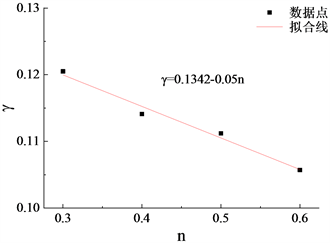(b) Y主轴方向

Figure 10. Relationship between axial force influence coefficient and axial compressive ratio

图10. 轴压力影响系数与轴压比之间的关系

$\gamma$ 与n的关系为：X方向： $\gamma =0.1713-0.04n$ ；Y方向： $\gamma =0.1342-0.05n$。

确定待定系数后的SRC空间边节点核心区X和Y主轴方向抗剪承载力计算公式为：

$V_{j,x}=\left(0.1713-0.04n\right)\psi f_c{b}_j{h}_j+f_{yv}\frac{A_{sv}}{s}\left(h_0-{a^{\prime }}_s\right)+\frac{f_{sw}{h}_w{t}_w}{\sqrt{3}}$ (18)

$V_{j,y}=\left(0.1342-0.05n\right)\psi f_c{b}_j{h}_j+f_{yv}\frac{A_{sv}}{s}\left(h_0-{a^{\prime }}_s\right)+\frac{f_{sw}{h}_w{t}_w}{\sqrt{3}}$ (19)

5.3. 节点核心区抗剪承载力计算

通过数值模拟获取了型钢混凝土空间边节点柱端水平极限承载力与加载角度之间关系的数学表达式，由于核心区水平抗剪承载力与柱端水平极限承载力成正比，因此，可将柱端水平极限承载力计算模型引入SRC空间边节点核心区抗剪承载力计算公式中，即：

${\left(\frac{V_j\sin \theta }{V_{j,x}}\right)}^2+{\left(\frac{V_j\cos \theta }{V_{j,y}}\right)}^2=1$ (20)

式中， $V_j$ 为空间节点核心区沿加载角度方向的抗剪承载力； $V_{j,x},V_{j,y}$ 分别表示节点核心区X和Y主轴方向抗剪承载力。

将式(20)进行转化可得式(21)，由式(18)、(19)计算出 $V_{j,x},V_{j,y}$，代入加载角度 $\theta$，即可计算出SRC空间边节点核心区沿加载角度方向的抗剪承载力。

$V_j=\frac{V_{j,x}{V}_{j,y}}{\sqrt{V_{j,y}^2{\sin }^2\theta +V_{j,x}^2{\cos }^2\theta }}$ (21)

将核心区抗剪承载力理论计算值 $V_{j,c}$ 与表3节点核心区极限水平剪力数值模拟值 $V_{j,t}$ 进行比较，如表5所示。由表可知，计算值与数值模拟值总体吻合良好，可见本文提出的SRC空间边节点核心区抗剪承载力计算公式不仅具有明确的物理意义，同时具备较高的计算精度。

Table 5. Comparison between theoretical and numerical simulation values for shear capacity of joints (Unit: kN)

表5. 节点受剪承载力理论值与数值模拟值的比较(单位：kN)

6. 结论

通过SRC空间边节点受力性能分析与抗剪承载力计算方法研究，得出以下结论：

1) 基于已有试验建立的SRC平面节点有限元计算模型计算结果与试验结果吻合较好，模拟中的不理想之处表现为滞回曲线的捏拢程度较差，但可以准确反映该类型节点的受力状况与特征点数值。

2) 分析不同轴压比和空间加载角度对SRC空间边节点受力性能的影响。随着加载角度增加，峰值荷载增大，滞回曲线饱满程度降低；随着轴压比增大，峰值荷载减小，对应的位移减小，且峰值点后节点强度退化加快。斜向加载下空间边节点在负向加载时承载力降低，强度退化加快，原因是负向加载缺少有效约束。

3) 通过扩大参数分析，得出柱端水平极限荷载与加载角度之间呈椭圆形分布关系。通过坐标系转化，基于椭圆曲线公式提出正向加载和负向加载下柱端极限荷载与加载角度关系的数学表达式。

4) 将SRC空间边节点沿两主轴方向分解为T形与十字形构件，利用数值模拟得出的数据，建立SRC空间边节点在斜向加载下核心区抗剪承载力计算公式，公式综合考虑加载角度、轴压比和正交梁约束等因素的影响，计算值和模拟值吻合较好，验证了公式的准确性与适用性。

基金项目

长安大学中央高校基本科研业务费专项资金资助(300102129721)；长安大学开放创新实验室项目(2018CXSY06)。