基于COMSOL仿真解释“隐形的瓶子”圆柱绕流现象

Explain the Phenomenon of Flow around the Cylinder of “Invisible Bottle” Based on COMSOL Multiphysics

摘要: 针对瓶子后方蜡烛熄灭现象，将所研究的流体空气看作不可压缩流体，引入二维粘性不可压缩流体的Navier-Stokes方程，利用COMSOL Multiphysics软件构建圆柱绕流仿真模型，讨论影响瓶子后方蜡烛熄灭的因素。对雷诺数、蜡烛位置、障碍物形状不同影响因素情况下圆柱绕流模型进行数值模拟，并给出三维情况下的圆柱绕流仿真模型。

Abstract: Aiming at the extinguishing phenomenon of the candle behind the bottle, the studied fluid air is regarded as an incompressible fluid, and the Navier-Stokes equation of two-dimensional incom-pressible viscous flow is introduced. The simulation model of the flow around a cylinder is con-structed by using COMSOL Multiphysics software, and the factors affecting the extinguishment of the candle behind the bottle are discussed. The numerical simulation of the flow model around a cylin-der is carried out under the different influence factors of Reynolds number, candle position and ob-stacle shape, and the three-dimensional simulation model of the flow around the cylinder is given.

1. 引言

圆柱绕流问题一直是一个经典流体力学问题，与生活以及实际工程问题息息相关。基于2020年国际青年物理学家锦标赛(IYPT)的竞赛题目第二题 [1]，本文重点利用COMSOL Multiphysics软件进行数值模拟。通过圆柱绕流仿真案例分析该问题并讨论影响瓶子后方蜡烛熄灭的因素。

2. 模型构建

设研究的流体为不可压缩流体，引入二维不可压缩流函数，建立xy平面直角坐标系，其连续性方程为 [2]

$\nabla \cdot \stackrel{\rightharpoonup }{\upsilon }=0$ (1)

引入不可压缩流体N-S方程

$\rho \frac{\text{d}\stackrel{\to }{\upsilon }}{\text{d}t}=\rho \stackrel{\to }{f}-\nabla p+\mu {\nabla }^2\stackrel{\to }{\upsilon }$ (2)

显然圆柱绕流问题与雷诺数有关。Coutanceau [3] 采用物理模型试验首次揭示圆柱后尾流形态和雷诺数之间的对应关系。在不计流体可压缩性时，Coutanceau指出无限长(二维)光滑圆柱的周期性尾流形态取决于Re数。单圆柱绕流尾流流态随Re数的增加依次经历蠕动流、对称驻涡回流泡、层流态涡街、涡旋由层流向紊流的过渡态、紊流态涡街、涡街消失、重现紊流涡街等阶段所以圆柱绕流问题与雷诺数有关。随着雷诺数的增加尾流流态呈现出不同的流动形态 [4]。

综上所述，忽略蜡烛燃烧对空气产生的影响，猜想圆柱绕流问题与瓶子的直径、吹气瓶口径的大小、吹气瓶与瓶子的距离、瓶子与蜡烛的距离、瓶子的材料等因素有关。下面将利用软件来进行仿真模拟和探究。

3. 数值分析

由于蜡烛燃烧气流沿着竖直方向，对建立的二维仿真模型影响较小，建模时忽略蜡烛燃烧对周围气流的影响，采用COMSOL Multiphysics进行圆柱绕流仿真案例分析。在长15 cm，宽为5 cm的矩形空间中进行研究，介质为空气。为了提高计算精度，保证收敛速度，对圆柱周围进行局部加密 [5]，根据雷诺数大小构建层流瞬态模型。添加自由三角形网格，网格划分情况如图1所示。其中包含1个“域”、“8个边界”及“8个顶点”。求解的自由度数为25,561 (加1个内部自由度)。

Figure 1. Meshing situation around the cylinder

图1. 圆柱周围网格划分情况

3.1. 探究雷诺数对蜡烛熄灭的影响

圆柱绕流问题与雷诺数有关，根据圆柱雷诺数计算公式

${\mathrm{Re}}_D=\frac{UD}{\upsilon }$ (3)

其中U为流场特征速度(m/s)；D为特征长度(圆柱体特征长度为直径)； $\upsilon$ 为流体运动粘度(m²/s)。

3.1.1. 探究来流速度对蜡烛熄灭的影响

在15 cm × 5 cm的矩形空间中添加直径为1 cm的圆形作为所探究的对象，介质为空气。设置入口速度为0.04 m/s，此时雷诺数约为20，可以看到尾流中有一对稳定的弗普尔旋涡 [5]。通过增加入口速度改变雷诺数。设置入口速度为0.4 m/s，圆柱直径仍然为1 cm，此时Re = 200。可以观察到稳定的卡门涡街 [6] [7]。继续增加入口速度，设置入口速度为0.8 m/s，圆柱直径仍然为1 cm，此时雷诺数约为800，此时旋涡出现不规则现象，并表现出三维效应 [8]。

针对蜡烛熄灭原因，比较入口速度分别为0.04 m/s，0.4 m/s，0.8 m/s的模拟结果，通过图2~4的对比可以看到，则在距离一定，障碍物相同的情况下，吹气速度越大，后方速度较小的区域就越小，蜡烛位于速度较大区域的可能性就越大，蜡烛就越容易熄灭。

Figure 2. U = 0.04 m/s, Re = 20 velocity field

图2. U = 0.04 m/s, Re = 20速度场

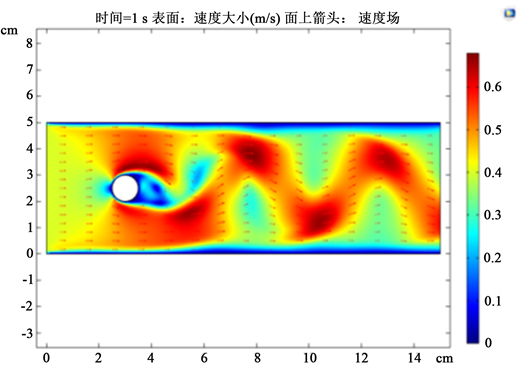
Figure 3. U = 0.4 m/s, Re = 200 velocity field

图3. U = 0.4 m/s, Re = 200速度场

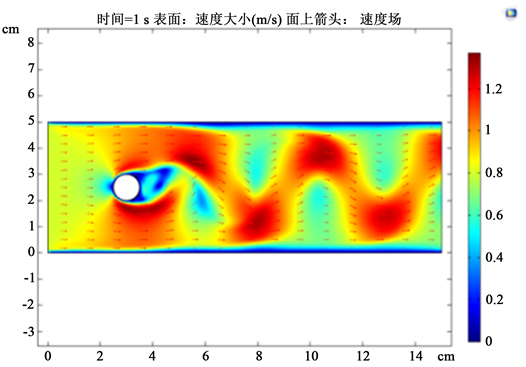
Figure 4. U = 0.8 m/s, Re = 800 velocity field

图4. U = 0.8 m/s, Re = 800速度场

3.1.2. 探究瓶子的直径对圆柱绕流的影响

改变圆柱绕流中圆柱直径D会使得雷诺数发生变化。圆柱直径变大，雷诺数增加。在矩形空间中分别添加直径为1 cm、2 cm、3 cm的圆形作为所探究的对象。设置入口速度为0.4 m/s，观察图5~7仿真结果。

通过COMSOL软件模拟我们可以看到，在曲率半径不是很大的情况下，圆柱直径越小，蓝色区域就越小，则在距离一定的情况下，蜡烛位于该蓝色区域的也就是速度小的区域可能性就越小，蜡烛越容易熄灭，与理论分析结果相符合。

Figure 5. D = 1 cm velocity field

图5. D = 1 cm速度场

Figure 6. D = 2 cm velocity field

图6. D = 2 cm速度场

Figure 7. D = 3 cm velocity field

图7. D = 3 cm速度场

3.1.3. 探究流体运动粘度对蜡烛熄灭的影响

当圆柱绕流所处环境介质改变时，即改变流体运动粘度时，根据雷诺数公式，流体运动粘度的介质越大，雷诺数越小。通过COMSOL Multiphysics软件改变介质，设置入口速度为0.2 m/s，圆柱半径为1 cm，其他变量不变，选取空气、水、植物油三种常见介质进行模拟。

通过观察图8~10圆柱后方蓝色区域大小，看到流体运动粘度越大的介质后方速度小的区域越小，如若后方有蜡烛，则更容易熄灭，与理论分析结果相符合。

3.2. 探究蜡烛位置对蜡烛熄灭的影响

设置入口速度为0.4 m/s，圆柱直径为1 cm时，只改变蜡烛距障碍物的距离，通过COMSOL软件模拟情况如图3所示。此时Re = 200，尾流相对稳定，若在后方放置蜡烛，蜡烛越靠近圆柱体的流体速度越小，越难以熄灭。但当蜡烛距离圆柱体足够远时，尾流对其影响逐渐减弱直至消失，此时蜡烛就难以熄灭。

Figure 8. Medium for air

图8. 介质为空气速度场

Figure 9. Medium for water

图9. 介质为水速度场

Figure 10. Medium for vegetable oil

图10. 介质为植物油速度场

3.3. 探究障碍物形状对蜡烛熄灭的影响

若将障碍物换成平板，当蜡烛放置在平板后面，从平板前面吹气时，蜡烛的火焰不会熄灭。流体被平板阻塞，不会绕到后面。这种被物体障碍分离的气体流动现象被称为“分离”。当平板相对较小时，可以产生一股在平板后面循环的弱流，这种气流被称为分离旋涡 [9]。

通过COMSOL模拟观察图11、图12可以清楚的观察到平板后方的速度明显较小，很难将蜡烛吹灭。

3.4. 分析圆柱后方回流现象

在预实验中观察到吹气的瞬间蜡烛火苗在熄灭之前会向水瓶方向移动。通过COMSOL在速度计算结果仿真模拟上添加面上箭头后，放大圆柱部分区域，图13可以清楚的看到在圆柱后方的速度方向朝向圆柱体一侧，这也是由于分离旋涡而产生的现象，模拟情况与实验相符合。

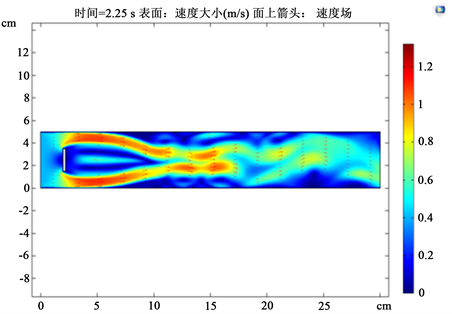
Figure 11. Velocity field when the obstacle is a flat plate

图11. 障碍物为平板时速度场

Figure 12. Velocity field after local amplification

图12. 局部放大后速度场

Figure 13. The direction of flow field around cylinder speed figure

图13. 圆柱周围流场速度方向

4. 模型补充——三维场圆柱绕流问题分析

在实际问题分析时，实验环境处在三维环境中，当雷诺数较小的时候，我们可以根据对称性将三维问题转化为二维问题方便实际问题的求解。但当Re = 800时，涡街出现不规则现象，并表现出三维效应。随着雷诺数的增加，圆柱周围的流场在沿圆柱展向方向上的脱落逐渐出现了不同步 [10]。

通过COMSOL构建三维场，在宽度为20 cm，深度为5 cm，高度为2 cm的三维空间中添加直径为1 cm高度为5 cm的圆柱体作为所探究的对象，介质为空气。根据此时的雷诺数更改模型，在湍流模型中选择添加自由四面体网格，网格划分情况如图1所示。其中包含1个“域”、“8个边界”及“8个顶点”。求解的自由度数为25,561 (加1个内部自由度)。如图14，此时Re = 3300可以看到三维现象。

5. 误差分析

该模型和理论公式建立于相对理想条件下。与COMSOL仿真相比，真实实验不存在边界条件，区域不封闭可能会有蜡烛燃烧等外界气流干扰；在模型构建中，为方便计算和可视化分析，选取的边界条件、壁面条件和初始条件是理想的并非实际的，且其流场并非均匀的。在数值计算和流场可视化中，应逐步减少对理想条件的依赖，使模拟情况更符合实际。

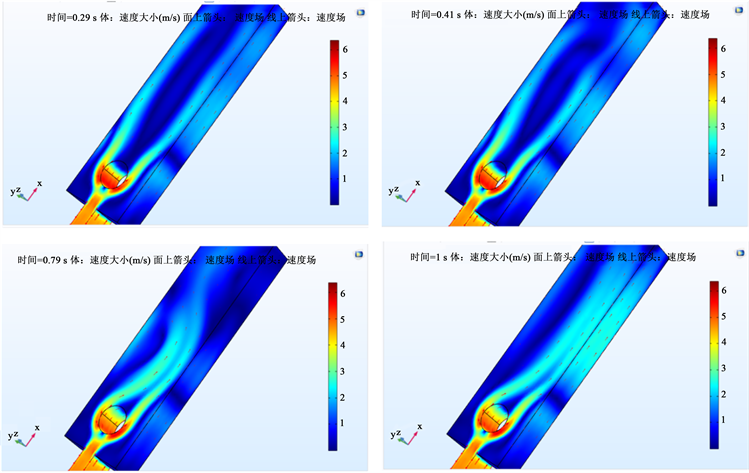
Figure 14. The three-dimensional flow around cylinder flow field in different time

图14. 三维圆柱绕流不同时刻流场图

6. 总结

本文通过COMSOL Multiphysics软件进行数值模拟，分析了以瓶子后方蜡烛熄灭为例的空气中圆柱绕流问题，直观清晰地得出改变参量后雷诺数改变，使瓶子后方尾流呈现出不同的流动形态，并针对实际问题构建三维模型，弥补二维模型在雷诺数较大的非对称情况的不足，通过仿真结果直观清晰地展示了三维尾流变化，对空气中圆柱绕流问题具有一定的工程价值。