我国碳排放权交易市场与高碳排放行业、新能源行业股票市场的联动性及风险传染研究

Research on the Dynamic Correlation and Risk Contagion between Carbon Emission Trade Market and the Stock Market of High-Carbon-Emission Industry & New Energy Resources Industry in China

摘要: 近年来，全球气候整体变暖趋势愈发严重，人类越来越重视节能减排问题，发展低碳经济已成为各国共识。为控制企业碳排放量，建立碳排放权交易市场是最有效措施之一。而随着我国统一碳排放权交易市场的建立，其作为一个新兴的投资市场也逐渐进入投资者的视野。本文选取我国上海、北京、广东和天津四个碳排放权交易试点市场作为碳排放权交易样本市场，并编制了两个行业股票指数作为股票样本市场指标，通过构建时变t-Copula-GARCH模型研究了两两市场之间的动态条件相关性。在此基础上，本文利用分段Granger因果关系检验分析了两两市场在不同时期的风险传染性的变化。实证研究发现：在正常情况下，碳交易价格的变化对高碳排放行业股指存在负向影响；当美国宣布退出巴黎气候条约时，以及在我国新冠疫情得到控制后的复工复产阶段，高碳排放行业股指的变化对碳交易价格存在正向影响；新能源产业的股指收益率受国家政策影响较大，且新能源行业股指的变化对碳交易价格存在负向影响。基于研究结果，本文分别对投资者、企业主体及政府提出了一系列参考和建议。

Abstract: In recent years, the trend of global warming has become increasingly significant. People are paying more and more attention to energy conservation and emission reduction, and the development of low-carbon economy planning has become the consensus of certain countries. In order to control the carbon emissions of enterprises, the establishment of carbon emission trading market is one of the most effective measures. With the construction of China’s unified carbon emission trading market, it has gradually entered the horizon of investors as a brand-new investment channel. We selected four pilot carbon emission trading markets in China, Shanghai, Beijing, Guangdong and Tianjin, as sample markets for carbon emission trading, and two separate industry stock indexes were compiled as sample market indexes. By constructing a time-varying t-Copula-GARCH model, we studied the dynamic conditional correlation between the two markets in a specified sample interval. On this basis, the change of risk contagion in two markets in different periods was analyzed respectively by using Piecewise Granger Causality Test. Through empirical research, we could draw the following conclusions. Firstly, under normal circumstances, the change of carbon trading price has a negative impact on the stock index of the high-carbon-emission industry. Secondly, When the United States announced its withdrawal from the Paris Climate Treaty, as well as the resumption of work and production after the COVID-19 epidemic in China was under control, the change of high-carbon industry index had a positive impact on carbon trading price. Finally, the return rate of new energy industry stock index is greatly affected by national policies, and the change of high-carbon-emission industry stock index has a negative impact on carbon trading price. Additionally, based on the research results, we put forward a series of suggestions and conferences for investors, enterprises and the government.

1. 引言

目前世界上公认最直接、最有效并被广泛采用的限制碳排放的方法，是建立在总量控制与交易机制(Cap-and-Trade)下的碳排放权交易市场。在总量交易制度下，企业必然希望最大限度地降低履约成本而积极参与碳排放权交易，交易后企业减排成本和社会总减排成本均会下降 [1]。这一市场机制通过将企业的碳排放量转化为具有稀缺性的商品，提高了企业对于碳资产管理的重视程度，进而引导企业技术和资金向低碳领域发展。

目前，我国是二氧化碳排放总量最大的国家，也是清洁能源发展机制(Clean Development Mechanism, CDM)最具市场发展潜力的国家，但我国在碳排放权交易市场交易体系领域的理论研究以及实践工作的开展却相对较晚。国家发改委办公厅于2011年正式批准北京、深圳、广东、上海、湖北、天津和重庆七个省市开展碳排放权交易试点工作，2013年后各试点市场陆续启动碳排放权交易。自此之后，我国各碳排放权交易试点市场发展迅速，市场机制和交易体系逐年完善 [2]。基于试点工作的成功实践，我国于2017年12月宣布正式开始建设全国统一碳排放市场，并以电力行业为出发点，于2021年1月1日启动第一个实质性碳交易的履约周期。而要建设全国统一的碳交易市场，最关键的是发展并完善碳价机制，良好的价格机制是促进碳排放权交易市场健康发展的必要前提 [3]，其中重要的一步就是探究影响碳排放权交易市场价格的因素，尤其是需要关注其他市场与碳排放权交易市场的联动性及相互影响关系。Oberndorfer等(2008)就曾研究发现碳交易市场的价格波动所产生的效应会通过影响公司股价，从而影响其股票收益率 [4]。

2021年，在“碳中和”、“碳达峰”战略背景下，我国正式启动建设全国统一碳排放权交易市场计划，而随着碳排放交易机制不断完善、交易主体不断扩大，碳排放权市场将有望成为投资者新的投资方向以及企业新的融资渠道。所以，本文旨在通过研究我国碳排放权交易市场与我国高碳排放行业、新能源行业股票市场的联动性及两两市场之间的风险传染性，为投资者投资这一新兴市场的行为提供参考建议，并为相关企业制订碳资产管理策略、政府监管市场间风险传染提供一定的建议。

2. 文献综述

碳排放权交易市场与股票市场是两个独立、完整的市场，其交易产品、交易机制也不尽相同。但两者均与企业的生产成本和利润分红息息相关，故极有可能存在深层次的联系。陶春华(2015)的研究提出：碳排放权交易市场能发挥资源配置功能，提高高碳排放量企业的融资成本，引导社会资本流向低碳企业，鼓励并引导产业结构优化升级和经济增长方式的转变，进而影响股票市场 [5]。

目前学术界对于碳排放权交易市场收益率与股票收益率的相关性研究结论不一，大致分为三类。一种观点认为碳排放权交易市场收益率与股票收益率之间呈负相关性。Huang (2012)发现欧盟碳排放权交易价格下降时，新能源企业的预期利润会上升，从而拉升企业的股价 [6]。陶春华(2015)通过构建VAR模型研究了碳排放权交易市场与股票市场的价格溢出效应，并发现高碳排放行业受碳交易价格影响较大，两者呈现负相关的关系 [5]。第二种观点则认为碳排放权交易市场收益率与股票收益率之间呈正相关性。Smale等(2006)以及Werner (2012)都认为，虽然总量控制的减排政策会导致企业成本增加，但是这些成本大部分最终都由消费者承担，且碳配额的直接分配将直接给企业带来净利润，并实证发现大多数参与减排的产业会出现盈利 [7] [8] [9]。Oberndorfer等(2008)的研究表明，碳分配期货价格与电力行业等高碳排放量企业的股价呈正相关关系 [4]。Venmans (2015)通过对欧洲碳排放价格与所有市场指数中的成份股价格的关系进行研究，指出大部分公司的股价对碳排放权价格存在正向的影响 [8]。第三种观点认为短期内两市场负向影响，长期看则是正向影响。这是因为碳排放权交易体系从表面看增加了购买者的短期可变成本，故在短期内使得企业利润缩减；但长期来看，碳排放权交易能有效促进企业减排控污技术的创新，从而减少企业的长期治污成本 [10]。陈向阳和何海靖(2021)的研究表明碳排放权交易对企业价值的影响具有双重效应，即短期的环境成本增加效应和长期的投资激励效应 [11]。

综上所述，目前分析碳排放权交易市场与股票市场的相关性的文献大多数以欧洲碳排放交易体系(EU ETS)的交易数据为样本，尽管研究西方国家的碳排放权交易市场情况对我国碳排放权交易市场的发展也有一定的借鉴意义，但由于我国与西方国家的根本经济制度、社会生活水平、购买力水平、制造业结构等因素有较大差异，其研究结果并不能直接应用于我国碳排放权交易市场的分析 [12] [13]。并且，聚焦到我国股票市场，目前对中国碳排放权交易市场和中国股票市场的联动性研究大多以单一碳排放权交易市场或单一股票市场指数作为研究对象，对于某一特定行业板块股票指数与碳排放权交易价格联动性的研究几乎空白。

故综上所述，本文的创新点如下：第一，目前缺乏对我国个别行业板块股票指数与碳价格联动性的研究，而本文着眼碳排放权市场价格收益率分别与高碳排放行业、新能源行业股票指数收益率的联动性，并基于不同时期分析两两市场间风险传染性的变化，一定程度上填充了该领域的空白；并且本文还根据实证研究结果分别对政府、相关行业企业以及投资者提出了一系列建议，具有一定的现实意义。第二，本文选用时变Copula-GARCH模型和分段Granger因果关系检验分别研究了两市场之间的动态条件相关性和风险传染效应，能够反映两市场间联动性和风险传染性的动态变化。第三，由于单一行业的股价指数无法代表整个高碳排放行业和新能源行业的整体情况，故本文分别编制了高碳排放行业股票价格指数和新能源行业股票价格指数，能够较好地反映整个高碳排放行业和新能源行业的股价波动情况；并且由于单个碳试点市场的价格也无法反映我国整体碳价格变化，故本文也选取了四个有代表性的碳试点市场，并在此基础上编制了我国碳排放权交易市场价格指数，对之后全国统一碳排放权交易市场与高碳排放行业、新能源行业的理论分析具有较大的参考价值。

3. 理论假设与作用机理分析

碳排放权交易市场与股票市场是两个独立、完整的市场，其交易产品、交易机制也不尽相同。但两者均与企业的生产成本和利润分红息息相关，故极有可能存在深层次的联系。一方面，在碳排放权交易市场中，碳商品的价格变化能够加强企业对于环保因素的重视程度，实现环境外部成本内部化，从而通过信息传递效应影响投资者对企业利润的预期，进而影响股票市场的收益率；另一方面，碳排放权交易市场提高了高碳排放量企业的融资成本，进而发挥资源配置功能，引导社会资本流向低碳环保企业，鼓励并引导产业结构优化升级和经济增长方式的转变，进而影响股票市场。故基于以上理论，本文提出以下假设。

假设1：碳交易价格的变化对高碳排放行业股指存在负向影响

在两个市场主体中，由于我国碳排放权交易市场建立时间较晚，交易机制尚不完善，其对政策的敏感性相对股市来说更高，即在现阶段政府对于碳交易市场的作用和控制能力远高于其他资本市场与之联动的影响。并且，目前全国统一的碳排放权交易市场刚刚进入第一个正式履约周期，市场不稳定因素依然居多。由于碳排放权交易市场价格的主要决定因素是外生变量碳配额，故当碳配额紧缩时，碳排放权出现供不应求而导致其价格上涨，高碳排放企业将面临成本上升、利润下降的压力，那么这些企业分红的减少就将使投资者产生其股价下跌的预期，进而造成高碳排放行业的股指下跌。

假设2：高碳排放行业股指的变化对碳交易价格存在正向影响

由于高碳排放行业的产能上游来源主要是煤、石油、天然气等化石燃料资源，当供给端产能资源充足时，企业倾向于扩大生产规模、提高企业利润、增加企业分红。此时在股市上的体现为，投资者预期高碳排放行业企业股价上涨，从而推动股价上涨；同时由于产能提高，碳排放量增加，在碳配额总量一定的前提下，碳排放权出现供不应求的情况，从而拉升碳排放权交易价格。

假设3：新能源行业股指的变化对碳交易价格存在负向影响

当新能源行业受到政策扶持、市场份额扩大等因素刺激时，投资者会产生新能源行业利润增加的预期，从而导致企业股价上涨；同时由于上述利好新能源行业的政策对于高碳排放行业往往是利空因素，导致高碳排放行业预期市场份额相对缩小而减少产能，减少对于化石燃料和碳排放额的需求，碳排放权交易市场倾向于出现供过于求的情况，最终导致碳交易价格的下跌。

综上所述，碳排放权市场价格与两个行业股票行业指数的相关性理论假设较为复杂，呈现出一个非对称的相关性影响机制，其路径图如图1所示。然而上述理论假设是否成立，还需要进一步的实证研究与分析。

Figure 1. Correlation influence path between carbon emission trade market price and stock index of two industries

图1. 碳排放权市场价格与两个行业股票指数相关性影响路径图

4. 模型构建与指标构建

4.1. 时变Copula-GARCH模型

建立时变Copula-GARCH模型通常有以下步骤：1) 对GARCH模型进行拟合以确定边缘分布。由于金融时间序列往往呈尖峰厚尾状，故通常采用GARCH模型进行建模分析。GARCH模型的残差序列分布类型不尽相同，故需要建立不同残差分布的GARCH模型进行比较并确定最优模型；2) 建立合适的GARCH模型并得到边缘分布后，使用最优的Copula模型进行拟合，即求解联合概率分布；3) 使用两阶段估计法(IFM)构建时变Copula-GARCH模型。

4.1.1. GARCH模型的拟合

以下模型建立过程中，以“CNP”代表高碳排放行业股指，“CPP”代表新能源行业股指，以“cavg”代表碳排放权交易市场平均价格。

令 $R_{\text{stock},t}\left(\text{stock}=\text{CNP},\text{CPP}\right)$ 为高碳排放行业和新能源行业股票指数在t时刻的收益率， $R_{\text{cavg},t}$ 为碳排放权交易市场价格在t时刻的收益率。GARCH(1, 1)模型表述为：

$R_{i,t}={\mu }_{i,t}+{\displaystyle {\sum }_{j=1}^p{\phi }_{i,j}{R}_{i,t-j}+a_{i.t}}$ (1)

$a_{i,t}={\sigma }_{i,t}{\epsilon }_{i,t},{\epsilon }_{i,t}~T\left({\nu }_i\right)$ (2)

${\sigma }_{i,t}^2={\alpha }_{i,0}+{\alpha }_i{\alpha }_{i,t-1}^2+{\beta }_i{\sigma }_{i,t-1}^2$ (3)

$t=1,2,\cdots ,T$

其中： ${\alpha }_{i,0}>0$， ${\alpha }_{i,t}\ge 0$， ${\beta }_{i,t}\ge 0$ ； ${\phi }_{i,j}$ 表示模型的待估计参数； $R_{i,t}$ 和 ${\mu }_{i,t}$ 分别表示投资组合中资产的实际回报率与预期回报率；p是自回归模型的阶数，根据后续实证中的拟合效果，由于碳排放权价格对数收益率序列具有自相关效应，故需要通过指定其边缘分布为AR(1) - GARCH(1, 1)来消除其数据自相关，即自回归阶数p = 1；而对于两个行业股指对数收益率序列，由于不存在自相关现象，故直接对其边缘分布使用GARCH(1, 1)进行拟合，即自回归阶数p = 0； $\left\{{\epsilon }_{i,t}\right\}$ 是服从标准化t分布的独立同分布随机变量(即白噪声扰动序列)， ${\nu }_i$ 是其t分布的自由度； ${\sigma }_{i.t}^2~\text{GARCH(}1,1)$ 保持平稳性的充要条件为 ${\alpha }_i+{\beta }_i<1$。

4.1.2. 使用两阶段估计法(IFM)构建Copula-GARCH模型

本文使用Joe (1997)提出的两阶段估计法(IFM)，即首先对两个边际分布的参数进行极大似然估计，并得到 ${\mu }_t=F_{\text{cavg}}\left(R_{\text{cavg},t}|{\psi }_{t-1}\right)$ 和 ${\upsilon }_t=F_{\text{stock}}\left(R_{\text{stock},t}|{\psi }_{t-1}\right)$ 的估计值，然后将这些估计值用于 $R_{\text{cavg},t}$ 和 $R_{\text{stock},t}$ 之间相依结构的估计，即对Copula函数的参数进行极大似然估计。

首先取时间序列样本 $\left(z_{\text{stock},t},z_{\text{cavg},t}\right)$， $t=1,2,\cdots ,T$，分别对两个边际分布的参数进行极大似然估计：

${\theta }_{\text{stock}}^{^}=\arg {\max }_{{\theta }_{\text{stock}}}{\displaystyle {\sum }_{t=1}^T\ln f_{\text{stock},t}\left(z_{\text{stock},t}|{\psi }_{t-1};{\theta }_{\text{stock}}\right)}$ (4)

${\theta }_{\text{cavg}}^{^}=\arg {\max }_{{\theta }_{\text{cavg}}}{\displaystyle {\sum }_{t=1}^T\ln f_{\text{cavg},t}\left(z_{\text{cavg},t}|{\psi }_{t-1};{\theta }_{\text{cavg}}\right)}$ (5)

随后对Copula函数的参数进行极大似然估计：

${\theta }_c^{^}=\arg {\max }_{{\theta }_c}{\displaystyle {\sum }_{t=1}^T\ln c\left({\mu }_t^{^},{\upsilon }_t^{^};{\theta }_c\right)}$ (6)

Patton (2001)依据ARMA(1, 10)过程，针对t-Copula模型的待估计参数提出了相关系数的方程形式：

${\rho }_t={\Lambda }^{^}\left[w_t+{\beta }_t{\rho }_{t-1}+a_t\frac{1}{10}{\displaystyle {\sum }_{j=1}^{10}{T}^{-1}\left(u_{t-j};v\right)T^{-1}\left(v_{t-j};v\right)}\right]$ (7)

公式中的函数 ${\Lambda }^{^}=\left(1-{\text{e}}^{-x}\right)/\left(1+{\text{e}}^{-x}\right)$ 的运用可以确保方程的结果区间落在 $\left[-\text{1},\text{1}\right]$ 中。 $T^{-1}\left(;v\right)$ 是自由度v的t分布的累积分布的逆函数，此处假设自由度v不变。

通过上述建模过程，最终的动态条件相关性系数 ${\rho }_t$ 可由参数 $v,\alpha ,\beta$ 的最大似然估计间接得到，模型保持平稳性的充要条件为： $\alpha +\beta <1$。

4.2. 指标构建

在本节，本文将构建高碳排放行业、新能源行业股票指数作为行业股票市场的测量指标。但由于在各大指数编制公司提供的现有产品中没有可以囊括整个高碳排放行业以及新能源行业的指数，故本文需要自行编制高碳排放行业股票指数和新能源行业指数两个股价指数。其步骤主要分三步：首先分别确定高碳排放行业股指和新能源行业股指需要涵盖的具体行业；随后选定指数编制公司现有指数产品中的成份股并进行相应处理，得到自定义指数的成份股；最后仿照沪深300指数的编制方案，制定相应的加权方案和其他编制规则 [14] [15]。

具体实施步骤如下所示：

1) 在高碳排放行业中选取碳排放量居于前列的八大行业如下：煤炭开采行业、火电行业、热电行业、石油开采行业、造纸行业、钢铁行业、有色金属行业和水泥制造行业。在Wind数据库中的申万行业指数中选择对应上述八个行业的行业指数：申万火电指数(851611.SI)、申万钢铁指数(801040.SI)、申万石油化工指数(801035.SI)、申万造纸指数II (801143.SI)、申万有色金属指数(801050.SI)、申万水泥制造指数II (801711.SI)、申万热电指数(851614.SI)、申万煤炭开采指数II (801021.SI)，并提取各行业指数成份股，剔除掉标有“ST”和“*ST”的个股以及主业务中70%以上不属于高碳排放行业的个股，得到最终的自定义指数成份股；

2) 对于新能源行业，Hvelplund F. (2016)和周君(2018)认为，新能源产业主要是依靠国家推行相应利好政策措施而获得快速发展的 [16] [17]。故选取对于高碳排放行业具备一定竞争力、且获得国家碳中和发展宏观政策扶持的产业如下：新能源发电行业、光伏设备产业、新能源汽车行业及其产业链。在Wind数据库的申万行业指数以及中证行业指数中选择对应上述三个行业的行业指数：申万光伏设备指数(857333.SI)、申万新能源发电指数(851615.SI)、中证新能源汽车指数(399976.SZ)，并提取各行业指数成份股，剔除掉标有“ST”和“*ST”的个股以及主业务中70%以上不属于新能源行业的个股，得到最终的自定义指数成份股；

3) 得到成份股后，在Wind金融终端中进行两个行业股票指数的编制。其中收益计算方式为全收益指数，加权类型参考沪深300指数的编制方案，采取流通股本结合标准分级靠档的方案，基点设为1000点，起始计算日期为2014年1月2日。为防止新股上市后由于炒作等不可控因素对整体指数造成影响，所有新股在上市后60个交易日后再计入指数。

5. 实证研究与结果分析

5.1. 样本数据及其基本特征

本文选取上海、北京、广东、天津四个碳排放权交易试点市场作为样本市场，选择上述四个碳排放权交易试点市场的原因如下：一是由于这四个碳排放权交易市场成立时间相近，前后均在一个月内相继成立并启动交易，而湖北、重庆、福建市场的成立时间均在至少半年后；二是经过数年的试点，该四个市场的成熟度、市场交易机制的完善度、纳入减排企业的范围更为相近；三是这四个市场的碳交易产品品种基本一致，类别单一，方便数据收集与处理，而深圳试点市场虽然是全国第一个成立的试点市场，但其交易品种较为多样化，在每一个履约周期都推出了新的碳配额方案并接收履约交易，而下一个周期仍可以结算上一周期的履约交易，故在数据处理方面不具有较大可行性 [18]。

选取上述四个试点市场的碳交易收盘价并取其算术平均值作为碳排放权市场价格，各试点市场交易价格数据来源为中国碳交易网(http://k.tanjiaoyi.com)。由于上述四个碳排放权交易试点市场于2013年年底成立，在成立初期，我国各试点地区的经济发展情况、能源结构和产业结构不同，各试点市场制定了不同的碳配额分配机制，故各市场价格割裂情况较为严重，碳排放权交易量也不甚稳定 [5] [19]。考虑到上述因素，本文根据实际情况，将样本日期定为2017年7月3日至2021年3月23日。

第四节中编制了高碳排放行业股票指数和新能源行业股票指数两个股价指数作为测量指标。股票市场有周末及法定节假日开闭市的时间限制，而碳交易市场的价格数据在上述股市闭市日期虽然并没有产生成交量，但是并不停止记录，各碳交易市场的记录规则也不完全一致。故本文对数据进行了日期的统一化处理，剔除了碳交易市场价格中日期重复的数据和明显记录有误的数据，以及碳排放权交易市场交易价格中对应股票市场闭市日期的数据，使碳交易市场价格数据与两个行业股价指数的样本日期完全一致。

对得到的三个时间价格序列进行价格走势图的绘制，其结果分别如图2~图4所示：

Figure 2. Trend of carbon emission trade market price

图2. 碳排放权交易市场价格走势图

由上图2的碳价格走势图可知，从2017年7月到2020年8月，碳交易价格整体呈上升趋势，其中在2018年底和2019年底出现了短暂的回撤，在2020年底以及进入2021年后，由于全国统一碳排放权交易市场正式进入履约周期等宏观因素，导致各试点市场碳价格出现下滑。

Figure 3. Trend of high-carbon-emission industry stock index

图3. 高碳排放行业股票指数走势图

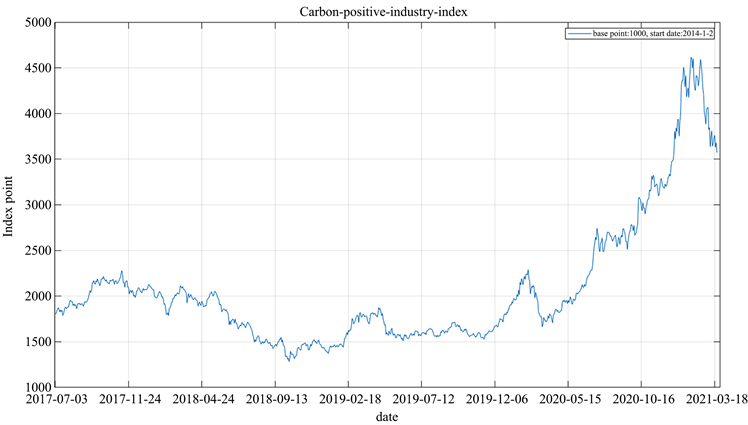
Figure 4. Trend chart of new energy industry stock index

图4. 新能源行业股票指数走势图

从图3、图4可以得到，两个行业指数的变化周期基本一致，均在2017年年底达到高点；随后均在2018年受中美贸易战和全球股市暴跌等因素影响而经历了下行行情，2019年年初触底反弹，随后进入几个月的横盘整理阶段，在2019年年底经历快速上涨后，由于新冠疫情的原因又快速下滑，直到4月份后由于国内疫情基本得到控制以及央行实行宽松的货币政策等因素的作用，我国股市进入一段牛市行情，一直持续到2021年春节前，春节后则又是连续下行。

对以上三列价格时间数据取日收益率作为时间序列样本，收益率算法采取对数收益率，即：

$r_t=\ln \frac{p_t}{p_{t-1}}$

对得到的三个时间序列进行描述性统计分析，得到结果如表1所示。

Table 1. Descriptive statistical results

表1. 描述性统计结果

注：1) 本表参数由Eviews9和R语言3.6.3得出；2) 变量CAVG表示碳排放权交易市场均价的对数收益率；CNP为高碳排放行业股票指数的对数收益率；CPP为新能源行业股票指数的对数收益率。后文同理；3) 表中数据为各项检验的p概率值，^***表示在1%的水平下拒绝原假设，^**表示在5%的水平下拒绝原假设，^*表示在10%的水平下拒绝原假设；4) 表中数据分布使用R语言计算得出，单位根检验1和单位根检验2分别使用“unitrootTest”计算McKinnons检验统计量和“adf.test”计算Augmented Dickey-Fuller检验统计量，原假设H0均为存在单位根(即序列不平稳)；自相关检验1和自相关检验2分别使用“Box.test”计算Box-Pierce检验和Ljung-Box检验计算Q统计量，原假设H0均为最多滞后1阶的序列自相关系数等于零；异方差检验使用“ArchTest”进行Lagrange Multiplier检验异方差，原假设H0是序列没有ARCH效应；正态分布检验使用“shapiro.test”进行Shapiro-Wilk检验正态分布，原假设H0是序列服从正态分布。

根据表1结果，由单位根检验得知，三个收益率序列均为平稳序列；通过Shapiro检验和Jarque-Bera统计量，可发现上述三个收益率序列均不服从正态分布，故可以使用GARCH模型进行拟合；根据异方差检验可得知，三个收益率序列均存在ARCH效应；自相关检验结果显示，两个行业指数收益率CNP和CPP不存在自相关，而碳排放权交易市场价格收益率CAVG在10%的置信水平下存在自相关，故有必要对CAVG序列进行AR-GARCH模型的拟合，CNP和CPP两个行业指数收益率则直接进行GARCH模型的拟合。模型的构建过程与结果已在第四章中阐述。

5.2. 碳排放权交易市场与行业指数动态条件相关系数分析

本节分为三部分：第一，构建AR模型对CAVG序列进行拟合，以消除其自相关性；第二，分别对三个收益率序列用GARCH模型进行拟合，得到三者各自的边缘分布序列；第三，采用时变t-Copula-GARCH模型分析CAVG分别与CNP和CPP的动态条件相关性。

在构建AR-GARCH(1, 1)模型对CAVG序列进行处理后，分别对三个序列进行t-GARCH模型和skew t-GARCH模型的拟合，并通过对比模型拟合的对数似然值、AIC、BIC准则值以及各参数的显著性水平，发现t-GARCH模型的结果相对更加显著，故使用t-GARCH模型进行拟合，其模型拟合结果见表2：

Table 2. Fitting results of t-GARCH model

表2. t-GARCH模型拟合结果

注：1) 上表提供了t-GARCH模型的参数估计结果，其中括号内参数为标准误。各参数在t-GARCH模型中的具体含义分别为：μ_i表示各资产的预期回报率；φ_i表示CAVG序列AR模型中的自回归项系数，该参数在CNP和CPP序列中为0；α_i表示上一期扰动项平方的系数；β_i表示扰动项方差的自回归项的系数，ν_i为扰动项序列服从标准化t分布的自由度；2) 本表参数均运用使用建模分析软件Matlab R2021a得到，使用的建模工具包是由Mantuos Vogiatzoglou于2010年提出的“Dynamic Copula Toolbox”工具箱；3) LL代表对数似然值。

上述三个序列的t-GARCH模型拟合结果中，α与β之和均小于1，表明t-GARCH模型的回归结果是稳健的。

随后，本文分别对碳排放权交易市场价格收益率CAVG与高碳排放行业股票指数收益率CNP、碳排放权交易市场价格收益率CAVG与新能源行业股票指数收益率CPP进行时变t-Copula模型的拟合，得到的Copula参数结果如表3所示。

Table 3. Fitting results of time-varying t-Copula model

表3. 时变t-Copula模型拟合结果

注：1) 上表提供了时变t-Copula-GARCH模型的参数估计结果，其中括号内参数为标准误。在时变t-Copula模型相关系数ρ_t的计算式(13)中，参数v为t分布的自由度，α为累加项的权重系数，β为上一期相关系数ρ_t−1的权重系数；2) 本表参数计算过程同表2。

从上表中可以看到，两个时变t-copula模型的拟合结果中，α与β的和均小于1，表明模型是稳健的。

Copula模型拟合的结果得到的动态条件相关系数走势图如图5和图6所示。

从图5、图6的动态条件相关系数时序图中可见，碳排放权交易市场与高碳排放行业股票市场的动态条件相关系数整体分布较为分散，但总体上大多时间仍呈负相关，负相关的峰值数量、峰值聚集性也较正相关更高；而碳排放权交易市场与新能源行业股票市场的动态条件相关系数整体分布较为集中，正负峰值区间的聚集性较好，分段断点较为明显。

Figure 5. Dynamic conditional correlation diagram between CAVG and CNP

图5. CAVG与CNP的动态条件相关性走势图

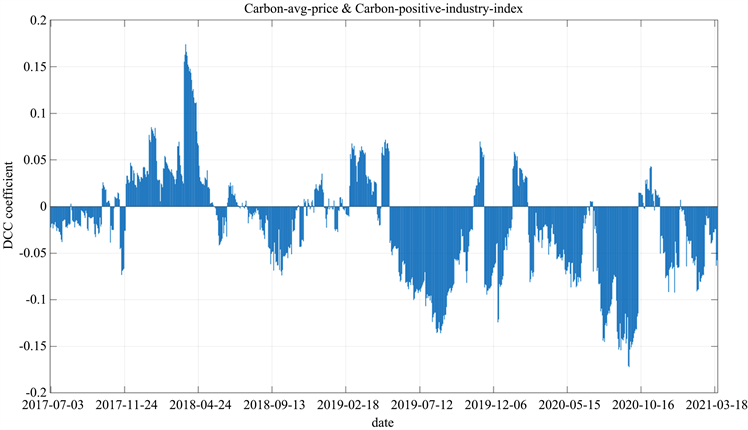
Figure 6. Dynamic conditional correlation diagram between CAVG and CPP

图6. CAVG与CPP的动态条件相关性走势图

5.3. 动态条件相关系数分段分析与分段Granger因果关系检验结果

在本节中，首先结合时序图的结构断点与实际的宏观经济事件将两个动态条件相关系数时序图分别分为七个阶段，随后将在每个阶段中进行Granger因果关系检验，以分析股票市场与碳排放权交易市场之间的风险传染因果关系，并结合实际宏观经济事件分析时序图中各阶段的动态条件相关系数分布情况。

5.3.1. 碳排放权市场价格收益率与高碳排放行业股票指数收益率

Figure 7. Dynamic conditional correlation coefficient distribution of CAVG and CNP

图7. CAVG与CNP的动态条件相关系数分布图

对动态条件相关系数时序图选取正负峰值区间，得到动态条件相关系数正、负峰值分布情况，如上图7所示。根据动态条件相关性峰值区间分布以及结合我国股市大盘拐点、中美贸易战、新冠疫情等宏观经济节点进行分段，得到最终的七个阶段如表4所示。

Table 4. Final subsection interval of CAVG-CNP logarithmic return rate

表4. CAVG-CNP对数收益率最终分段区间

在完成阶段划分后，对每一阶段都进行Granger因果关系检验，以分析每一阶段高碳排放行业股票指数与碳排放权交易市场之间风险传染的Granger因果关系。在此之前，先对不同阶段的收益率进行ADF检验，发现各阶段的各序列均为平稳序列，故均可以进行Granger因果关系检验。各阶段检验结果如表5所示。

Table 5. Granger causality test results of CAVG-CNP

表5. CAVG-CNP的Granger因果关系检验结果

1) 第一阶段~第三阶段(2017年7月~2019年3月)

首先，从碳排放权交易市场收益率与高碳排放行业股票指数收益率的动态条件相关系数分析得知，在第一阶段到第三阶段内，二者动态条件相关系数呈现出峰值分布分散、整体负相关的状态。

从分段Granger因果关系检验结果来看，在第一至第三阶段，两个市场的收益率理论上不存在显著的Granger因果关系。这可能是因为我国各碳排放权交易试点市场在纳入减排企业范围、市场交易主体以及制度设计等方面都存在显著的差异，导致各市场的价格与交易机制都处于较为分裂的格局，再加上许多政策的实施与交易机制还不够完善，导致市场交易量不够活跃。

其次，上述结果可能与前三个阶段中我国的股市大盘多为下行行情有关。在2018年，我国继续落实供给侧结构性改革，对于制造业实行“三去一降一补”方针，导致国内制造业投资份额显著减小，对制造业企业的股价造成不小的打击。同年，美方挑起贸易战，导致我国出口受到极大影响，我国服务、外贸行业受到一定程度的冲击。而2018年2月由美股暴跌引起的全球股市下挫，A股也是受影响的市场之一，新能源行业指数和高碳排放行业股票指数也都受大盘影响出现持续的下滑。

2) 第四阶段~第七阶段(2019年4月~2021年3月)

根据上文实证结果，2019年4月之后，显著峰值区间的聚集性明显加强，这意味着风险传染路径的稳定性在增强，而Granger因果关系的显著性增强也有效印证了这一点。其中第四、六、七阶段都出现了显著的单向Granger因果关系，第五阶段中两市场之间没有显著的Granger因果关系。

第四阶段和第七阶段时期，动态条件相关系数呈显著的负相关，且峰值分布均匀；同时这两个阶段内碳排放权交易市场的价格变动对高碳排放行业股票指数变动具有显著的Granger因果关系。这一结论较好地印证了上文提出的假设1，即正常情况下碳交易价格对高碳排放行业股票指数具有负向影响。

此外，宏观外部事件对两者间联动性也有一定的影响。2019年11月4日，美国政府通知联合国将退出《巴黎协定》；一年后，美国正式退出该气候条约，成为近两百个缔约方中唯一一个退出的国家。从动态条件相关系数时序图中可以看到，这两个时间点都出现了短期的正向峰值区间，其原因可能是由于美国的退出将造成投资者对于气候条约的稳定性产生质疑，从而会产生高碳排放行业要扩大生产的预期，企业对于碳排放额度的需求会暂时性的增大，进而推高了碳排放权价格。这一结论验证了假设2，当国际气候条约等宏观因素发生黑天鹅事件时，可能会在短期内暂时性地颠倒假设1中正常的风险传染路径，即由实体企业产能影响股票价格，进而影响碳排放权交易市场价格。

第五阶段涵盖了2020年年初的2月和3月，我国正处于疫情最为严重的时期。投资者的恐慌情绪作用在股市上，表现为大盘在2月、3月快速下滑，两个行业指数也随整体趋势一同下行。而由于当时全国各地的工厂已经停工停产，对于原材料的需求显著减少，高碳排放行业几乎没有生产，所以排放的二氧化碳量显著减少，导致碳排放额交易量较正常生产时期大幅下降，因此碳排放权交易价格并没有显著变化，也就没有与两个股票行业指数产生较大关联度。这就导致了在疫情最严重的两个月中两个行业指数收益率与碳排放权交易市场价格收益率的动态条件相关系数并不显著、峰值分布较为分散，且没有显著的Granger因果关系。

而随着我国疫情防控形势在进入5月份后基本得到有效控制后，动态条件相关系数又逐渐回到正常绝对值水平。第六阶段期间，我国处于疫情常态化防控阶段，全国范围内已基本完成复工复产。此阶段的Granger因果关系检验结果显示，存在从高碳排放行业股票指数收益率到碳排放权交易市场价格收益率的显著单向Granger因果关系。其原因是在复工复产阶段，制造业产能回升，再加上我国实行宽松的货币政策，促进国内对于制造业的投资力度加大，这些宏观政策能够进一步加强投资者对于企业产能提高而创造利润的预期，从而带动股票价格上涨，进而带动碳排放权交易市场价格推高。

5.3.2. 碳排放权市场价格收益率与新能源行业股票指数收益率

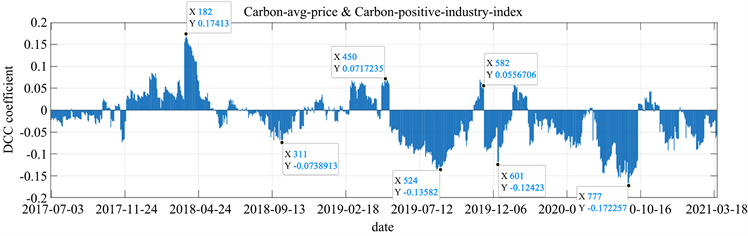
Figure 8. Dynamic conditional correlation coefficient distribution of CAVG and CPP

图8. CAVG与CPP的动态条件相关系数分布图

对动态条件相关系数时序图选取正负峰值区间，得到动态条件相关系数正、负峰值分布情况，如上图8所示。根据动态条件相关性峰值区间分布以及结合我国股市大盘拐点、中美贸易战、新冠疫情等宏观经济节点进行分段，得到最终的七个阶段如表6所示。

Table 6. Final subsection interval of CAVG-CPP logarithmic return rate

表6. CAVG-CPP对数收益率最终分段区间

在完成阶段划分后，在每一阶段对碳排放权市场价格收益率与新能源行业股票指数收益率进行Granger因果关系检验，从而能够进一步探讨在每一阶段新能源行业股票指数与碳排放权交易市场之间的风险传染的Granger因果关系，以判断两个市场之间在不同时间阶段的风险传染方向。对不同阶段的收益率进行ADF检验，发现各阶段的各序列均为平稳序列，故可以进行Granger因果关系检验。各阶段检验结果如表7所示。

Table 7. Granger causality test results of CAVG-CPP

表7. CAVG-CPP的Granger因果关系检验结果

1) 第一阶段~第三阶段(2017年7月~2019年2月)

由上述图表结果分析得知，第一阶段出现了显著的从碳排放权交易市场到新能源行业指数的单向风险传染机制，且动态条件相关系数呈负相关状态；而第二、三阶段两个市场之间的Granger因果关系并不显著。由于新能源产业受国家政策的影响更大，故以下以政策为切入点，分析第一阶段潜在的风险传染机制。

在2017年7月26日，国家发改委、能源局等十六部委联合印发《关于推进供给侧结构性改革化解煤电产能过剩风险的意见》，提出在“十三五”期间，全国停建和缓建煤电产能，淘汰落后产能，实施煤电超低排放改造、节能改造和灵活性改造；到2020年，全国煤电装机规模控制在11亿千瓦以内。与此相反，国家在2017年加大了对光伏产业的扶持力度。2017年5月，国家能源局下发《关于报送可再生能源“十三五”发展规划年度建设规模方案的通知》，提到“分布式光伏发电不受各地区年度新增建设规模限制”；同年10月，发改委及能源局下发《关于开展分布式发电市场化交易试点的通知》，提到要开展分布式发电市场化交易试点，推动隔墙售电。这一系列有利政策的推出，意味着分布式光伏补贴政策不受规模限制、模式稳定、盈利可预期，产业生产规模实现爆发式增长。

两个产业受到截然相反的政策影响，导致碳排放权交易市场投资者预期第一阶段碳配额需求会减少，从而碳交易价格出现持续的下行，并伴随数次短期的快速下挫；而相关政策结合碳价格波动的影响作用在新能源行业股票指数上，使得其行业股票价格持续上行，即使是在之后第二、第三阶段的18年2月全球股市暴跌，该行业指数的回撤幅度也远低于沪深300指数，恢复时间也更快，证明政策的利好以及碳价格的持续压低，有利于光伏产业等新能源行业的发展。

2) 第四、第五阶段(2019年2月~2020年3月)

根据上文实证结果分析可知，第四、第五阶段两市场并没有显著的Granger因果关系，其中第四阶段两市场相关系数呈正相关，其原因是2019年上半年我国股市经历一轮上涨行情，行业指数也随大盘上涨，而同时期国内制造业产能扩大，对于碳配额的需求也相应提高，故出现了两市场正相关的情形，但是没有显著的传染机制出现。而第五阶段后期为疫情最严重的时期，同上文高碳排放行业的分析同理，由于停工停产，碳排放额交易量较正常生产时期大幅减少，因此碳排放权交易价格并没有显著变化，从而并没有与两个行业指数产生较大关联度。

3) 第六、第七阶段(2020年4月~2021年3月)

根据上文实证结果分析可知，从第六阶段(2020年4月)开始，两市场间出现了显著的单向Granger因果关系，即从股票市场向碳排放权交易市场的单向风险传导。且通过动态条件相关系数时序图可发现，此阶段的相关系数呈现显著的负相关，且峰值聚集区间较为集中。

这一时期也是我国在碳排放权交易市场相关方面出台政策最为频繁的一个阶段。2020年11月，国务院办公厅印发《新能源汽车产业发展规划(2021~2035年)》，其中提出，到2025年，新能源汽车新车销售量达到汽车新车销售总量的20%左右，到2035年，纯电动汽车成为新销售车辆的主流，公共领域用车全面电动化，燃料电池汽车实现商业化应用。自2020年12月以来，中央经济工作会议、国家能源局能源工作会议、发改委全国发展和改革工作会议相继提出“做好碳达峰、碳中和”的相关工作部署。这一系列强力政策的出台，是第六、七阶段出现显著的单向Granger因果关系的最大因素。

这一现象验证了假设3，即当新能源行业受到政策扶持等因素刺激时，投资者预期新能源行业市场份额扩大、利润增加，从而导致企业股价上涨；同时由于上述利好新能源行业的政策对于高碳排放行业往往是利空因素，导致高碳排放行业预期市场份额相对缩小而减少产能，从而减少对于化石燃料的需求和对碳排放额的需求，碳排放权交易市场倾向于出现供过于求的情况，最终导致碳交易价格的下跌。此外，我国在2021年正式开启全国碳排放权交易市场的交易，造成各试点市场碳交易量下滑以及碳配额需求的减少，导致试点市场的碳价格下跌。

6. 结论与建议

本文通过构建时变t-Copula-GARCH模型研究了我国碳排放权交易市场分别与高碳排放行业、新能源股票指数的动态条件相关性，并利用Granger因果关系检验分析两个市场在不同时期风险传导关系的变化。实证研究发现。

第一， 正常情况下，当碳配额紧缩时，碳排放权出现供不应求而导致其价格上涨，高碳排放企业将面临成本上升、利润下降的压力，企业分红减少也将使投资者预期股价下跌，进而造成高碳排放行业的股指下跌，即碳交易价格的变化对高碳排放行业股指存在负向影响。

第二，当美国宣布退出巴黎气候条约时，以及在我国新冠疫情得到控制后的复工复产阶段，本应是碳交易价格变化引起股票指数波动的风险传染方向可能会颠倒，由实体企业产能影响股票价格，进而影响碳排放权交易市场价格。此时高碳排放行业股指的变化对碳交易价格存在正向影响。

第三，新能源行业极易受到国家政策影响，未来发展空间较大。当其受到政策扶持等因素刺激时，投资者会产生新能源行业市场份额扩大、利润增加的预期，从而导致企业股价上涨。同时由于利好新能源行业的政策对于高碳排放行业往往是利空因素，导致高碳排放行业预期市场份额相对缩小而减少产能，减少对于化石燃料和碳排放额的需求，碳排放权交易市场倾向于出现供过于求的情况，最终导致交易价格的下跌，即新能源行业股指的变化对碳交易价格存在负向影响。

基于以上结论，本文分别对政府、企业和投资者提出以下建议。

第一， 政府需要进一步完善全国统一碳排放权交易市场的交易机制，加强市场监管，并在对发电行业进行试点后，及时推广到更多高碳排放行业，使纳入减排范围的企业更加多样化，从而能够在一定程度上增强碳价格的稳定性。此外，对各减排企业提供的初始碳配额数量需要进行进一步的研究，以避免减排企业由于被分配了过多的碳配额而直接获得利润。

第二， 建议高碳排放行业的企业及时制定碳资产管理策略，从而能够有效帮助企业在“碳中和”、“碳达峰”时代应对公司生产成本和利润分红的变化，且需意识到加强碳减排技术的革新能力能够有效提升企业的长期价值，有利于公司股价的稳步上行。

投资者需要认识到我国的碳排放权交易市场还处于不成熟的阶段，其价格波动较股市更为剧烈，短线投资风险较大，且需认识到其与相关行业股票指数愈来愈强的联动性，不能忽视由于联动性带来的风险传染。同时，随着低碳经济概念的发展，新能源行业与碳排放权市场的联系也将越来越紧密，且由于两者存在负相关性，投资者可以考虑将其作为对冲风险的投资组合。同时，因为碳排放权交易市场相比股市更易受到宏观事件的冲击与国家政策的影响，所以投资者需要密切关注气候条约等宏观事件以及国家相关产业政策的出台，并需要对碳排放权市场的基本面形成较为成熟的见解。

参考文献