引力视角下出租车调度的增强学习模型

Reinforcement Learning Model of Taxi Dispatching under Gravity Perspective

摘要: 以互联网预约式叫车服务为背景，针对出租车运营中司乘匹配率低、乘客等车时间长和车辆空驶距离长的问题，通过类比万有引力模型，提出了空驶出租车巡游路线调度优化的增强学习控制方法。分别以备选目的地等车乘客数和当前位置空驶出租车数为对应位置的“质量”，而以两地间最短路径长度为两点间“距离”，定义两点间“引力”。通过引力大小，决策空驶车辆的目的地。通过引入增强学习理论，实现空驶出租车巡游路线决策的时空全局最优性，从而避免仅凭当前引力值大小决策路线的短视性。数值算例分析表明：新的调度方法不仅可以提高司乘匹配率和总的运营收入，而且可以减少总的空驶距离。

Abstract: In the setting of internet appointing taxi service, by analogizing the universal gravitation model, a control method of optimizing the cruising routes of vacant taxis was proposed to solve the problems of the low matching rate between taxis and passengers, the long average waiting time of passengers and the long travelling distance of vacant taxis. Using the number of waiting passengers as the mass of the corresponding alternative destination, the number of vacant taxis as the mass of current position, and the length of the shortest path between these two positions as their distance, the gravitation between these two positions can be defined. The next destination of a vacant taxi can be determined using the defined gravitation. By introducing the reinforcement learning theory, the decision of choosing the routes of vacant taxis possesses the global optimality. The short sight of deter-mining the routes only by the size of gravitation can also be avoided. The numerical example shows that the new taxi dispatching method can not only increase the matching rate between taxis and passengers and the total operation income, but also decrease the total travelling distance of vacant taxis.

1. 引言

随着手机叫车APP的普及，过去的扬招式出租车服务逐渐被各种互联网预约式叫车服务所代替。GPS和GIS技术也为出租车管理部门或运行公司提供了各种车辆运行实时信息和乘客需求信息。如何有效利用上述信息进一步提升出租车服务水平日益成为出租车运营公司谋求发展和重构核心竞争力的关键。如何利用现在信息通讯技术所带来的变化机遇实现运营服务各项关键指标的提升业已成为出租车运营企业面临的头号技术问题。在调度操作层面，企业面临的核心问题就是如何通过实时动态的空驶车辆调度控制，减少出租车空驶率和乘客的等车时间，并增加司乘匹配成功率和企业的运营收入。为了解决上述核心问题，本文以当前出租车行业发展的现状为背景，通过类比牛顿的万有引力模型，提出了一种新的空车路线选择方法，并结合增强学习理论实现对出租车服务系统的实时动态优化控制。

当一辆空驶的出租车选择下一时刻巡游目的地时，会考虑到达下一目的地后成功揽客的机率。成功揽客的机率取决于到达选定目的地时的等车乘客数量和当前位置与该目的地之间的距离。当然揽客成功与否也和同样选择该目的地的其他竞争出租车的数量相关。如果我们作如下的类比，将上述等车乘客数比做目的地的“质量”，当前车辆所在位置的空驶出租车数比做当前位置的“质量”，而将两地之间的行驶距离比做万有引力公式中两质量间的距离，我们就可以构建一个空驶出租车巡游路线选择的引力模型。通过两个位置间“引力”的大小决策最佳的巡游路线。

上述的引力模型可以对空驶出租车在当前时刻选择下一步巡游目的地提供一定的决策依据，但是未能利用整个出租车服务系统在时间空间上历史演变的经验，具有一定的短视性。因此，我们在巡游路线的决策中引入增强学习理论，内化决策的历史经验，提升短期决策的全局优化特征。

文献 [1] 指出通过出租车调度优化，出租车空驶费用可显著下降。文献 [2] 对出租车的定价范围与车队规模进行了分析。当前关于出租车服务系统的优化研究主要集中在运行模式分析 [3] [4] [5]、交通需求的弹性特征分析 [6]、市场中存在的竞争特征分析 [7]、乘客的随机需求分析 [8]、以及电招系统的选择上 [9] [10]。近年来，新的研究方向包括采用新的元胞网络研究出租车网络 [11]、考虑需求相应式服务 [12]，以及司机与乘客的匹配优化 [13]。近年来，研究者也开始关注机场的出租车调度问题，以期实现出租车与航班的匹配 [14] [15]。文献 [16] 利用增强学习理论对网格化的出租车实时动态调度进行了建模分析。已有研究主要关注静态的出租车系统，一般假设相关的出行需求和车辆巡游速度已知。总而言之，现有研究对动态的出租车运营系统特征考虑不足，较难满足今天出租车服务行业的变化需求。

2. 基本参变量与系统运行过程描述

2.1. 基本参变量

T是调度的实践间隔，即控制的时间步长。

k是将时间分段后的标记， $k\in \left\{0,1,\cdots ,K\right\}$ 。 $t=kT$ 是一个时间点， $KT$ 为总的调度时长。

$g\in G$ 是一个节点，即乘客的备选上下车位置；G是相关的节点集合。

$l\in L$ 是一条有向路段，一般由实际路段和交叉口构成；L为有向路段集合。

$p\in P$ 代表一个乘客，P是乘客的集合。

$v\in V$ 代表一辆出租车，V是出租车的集合。

$r_g$ 是T内节点g处乘客的生成率。

$r_{g,h}$ 是源于g处的一个乘客选择节点h作为目的地的概率。

${\bar{t}}_l$ 是出租车经过路段l的平均行程时间。

${\epsilon }_l$ 表示通过路段l时车辆的行程时间误差，服从均值为0而标准方差为 ${\delta }_l$ 的正态分布。

$g_p^O$ 是乘客p的出发起点。

$g_p^D$ 是乘客p的达到目的地。

$t_{p,1}$ 是乘客p利用APP请求服务的时刻。

$t_{p,2}$ 是p的登车时刻。

$t_{p,3}$ 是p到达目的地时的时刻。

$t_p^W$ 表示p的等车时间。当其出行需求可被出租车满足时， $t_p^W$ 等于 $t_{p,2}-t_{p,1}$ 。

$t_p^R$ 是p的乘行时间。当其需求可被满足时， $t_p^R$ 等于 $t_{p,3}-t_{p,2}$ 。

$d_p$ 表示p的起终点间的乘车距离。

${\eta }_v$ 为状态变量。当出租车v有乘客乘坐时， ${\eta }_v$ 等于1；否则，等于0。

$g_v$ 是v的标记节点。当有乘客p乘坐该车辆时， $g_v$ 等于 $g_p^D$ ；否则，为空驶出租车v已选取的最新目的地。

$t_v$ 是出租车v的等待激活时间。当有乘客p乘坐时， $t_v$ 表示该车距离网格 $g_p^D$ 的行程时间；否则， $t_v$ 为行驶到该车最新目的地的预期行驶时间。

$G_g$ 表示与节点g之间通过一条线段相连的节点集合。

$L_g$ 是所有以g为起点的路段集合。

$P_g\left(k\right)$ 是g处在时刻kT候车的乘客集合， $n_{g,P}\left(k\right)$ 是集合 $P_g\left(k\right)$ 的势；

$V_g^1\left(k\right)$ 是在时刻kT在g处空驶的出租车集合， $n_{g,V,1}\left(k\right)$ 是 $V_g^1\left(k\right)$ 的势。

$V_g^2\left(k\right)$ 为kT时刻以g为目的地的载客出租车集合， $n_{g,V,2}\left(k\right)$ 是 $V_g^2\left(k\right)$ 的势。

$V_g^3\left(k\right)$ 为kT时刻以g为目的地的空驶出租车集合， $n_{g,V,3}\left(k\right)$ 是 $V_g^3\left(k\right)$ 的势。

$c_0$ 是乘坐出租车的打车起步价。

$\stackrel{\rightharpoonup }{c}$ 表示超出 $d_0$ 后，出租车每公里的单价。

$\stackrel{⌢}{t}$ 是在起点可接受的最长等车时间。

2.2. 系统运行过程

为了简化后续的分析，我们对出租车服务的路网进行如下的抽象简化。首先，将现实中常见的出租车上下客地点，例如居民小区的出入口、购物中心出租车停靠点、办公大楼出租车停靠点和道路上划定的出租车上下客站点等，抽象为网络的节点。其次，将连接上述节点的车辆行驶路径抽象为出租车运行网络的路段。一般而言连接任意两个上下客节点的路径存在多条。我们采用一条抽象的路段代表其中的最短路径，作为服务网络中节点间的路段。最后，如果连接路段对应的最短路径需经过其他节点，则删除该路段。最后的操作可保证网络的节点仅与其附近的乘客上下客节点相连。

下面对出租车服务系统运行过程进行简述。

步骤1：假设当前时间点为 $kT$ ，当前考虑的节点为 $g\in G$ 。

步骤2：确定 $P_g\left(k\right)$ 和 $V_g^1\left(k\right)$ 。 $P_g\left(k\right)$ 由上一控制时刻未得到服务的等待乘客和 $k-1$ 时段新生成的乘客在排除超过最长等车时间 $\stackrel{⌢}{t}$ 的乘客后组成。 $V_g^1\left(k\right)$ 集合包含了由上一控制时刻在g处未得到匹配并选择g继续巡游的空驶出租车、当前时刻kT在g处完成载客服务的出租车以及在当前时刻kT抵达g的空驶出租车。

步骤3：对空驶出租车 $v\in V_g^1\left(k\right)$ 与等车乘客 $p\in P_g\left(k\right)$ 进行司乘匹配。首先对 $P_g\left(k\right)$ 中的乘客按照等车时间长短进行排序；其次，按照排序后的优先次序为乘客指派服务的出租车；最后，从 $P_g\left(k\right)$ 和 $V_g^1\left(k\right)$ 中删除已经得到匹配的乘客和出租车。此步骤中需记录匹配乘客的等车时间 $t_p^W$ 和匹配带来的运营收入，并更新车辆的特征 ${\eta }_v$ 、 $g_v$ 和 $t_v$ 。

步骤4：对空驶出租车 $v\in V_g^1\left(k\right)$ 的巡游路线进行决策。如果没有得到匹配，空驶出租车可以选择继续在该点巡游或驶向附近的节点。具体的决策方法将在下一节详述。

步骤5：如果G中所有节点已经被考虑，转步骤6；否则，从G中选取一个未被考虑节点作为新的当前节点，转步骤2。

步骤6：如果 $k<K$ ，令 $k:=k+1$ ，并任取节点 $g\in G$ ，更新相关的网络状态变量后转步骤2；否则，终止运行。该步骤中需更新的网络状态变量包括： $t_p^W$ 、 $t_v$ 和与节点相关的集合 $P_g\left(k\right)$ 、 $V_g^1\left(k\right)$ 、 $V_g^2\left(k\right)$ 和 $V_g^3\left(k\right)$ 。

3. 增强学习模型主要组成成分

3.1. 控制行为

在任意给定的控制时刻kT，当每一个节点可行的司乘匹配完成后，可能会出现部分节点还有乘客需要继续等待，而部分节点出现空驶的出租车。此时，需要对空驶出租车的巡游路线进行决策。设空载出租车v所在节点为g，那么v可以选择 ${\bar{G}}_g\equiv \left\{g\right\}\cup G_g$ 中的任意节点作为随后的巡游目的地。令 $V\left(k\right):=\left\{v|v\in V,{\eta }_v\left(k\right)=0\right\}$ 。对于空驶出租车 $v\in V\left(k\right)$ ，其选择的在kT时刻后的下一巡游目的地节点设为 $h_v\left(k\right)$ 。那么由所有 $h_v\left(k\right)$ ， $\forall v\in V\left(k\right)$ 构成的向量就是对应当前时刻kT的控制行为，表示为 $a\left(k\right)$ 或 $a_k$ 。 $a\left(k\right)$ 的可行域表示为 $A\left(k\right)$ 。

3.2. 控制信息

在增强学习理论中控制信息指的是系统运行中的随机和不确定性因素。出租车服务系统存在两种显著的随机因素。首先，每个节点乘客的生成是随机的，具有随机生成率 $r_g$ ， $\forall g\in G$ 和出行目的地分布概率 $r_{g,h}$ ， $\forall g,h\in G$ 。显然有 ${\displaystyle {\sum }_{h\in G}{r}_{g,h}}=1$ 和 $r_{g,g}=0,\forall g\in G$ 成立。假设 $r_g$ 的单位为(人/秒)，仿真试验中我们将逐秒生成(0, 1]间均匀分布的随机数 $R{N}_1$ 。如果 $R{N}_1\le r_g$ ，则生成一个以该时刻为生成时间的新乘客；否则，转下一秒的乘客生成分析。每一个新乘客依据轮盘赌的规则按概率 $r_{g,h}$ 选择其目的地。其次，出租车在路网中两点间的巡游时间具有随机性。受到其他社会车辆和交通控制条件的影响，出租车的巡游速度具有不确定性。为了模拟上述行程时间的不确定性，在仿真试验中，我们假设路网中任意路段l的行程时间 $t_l$ 由两部分组成，即 $t_l={\bar{t}}_l+{\epsilon }_l$ 。为了后续的表述方便，我们将上述随机因素用抽象向量 $\Delta$ 表示。向量 $\Delta$ 就是系统所需的控制信息。

3.3. 系统状态变量

系统状态变量是给定时刻对系统整体状态加以描述的各种特征因素构成的向量。我们将选择四种系统主要特征构成状态变量。

在给定的控制时间点kT，当节点 $g\in G$ 处所有的可能司乘匹配完成后，该点处空驶出租车的数目 $n_{g,V,1}\left(k\right)$ 和等车乘客数目 $n_{g,P}\left(k\right)$ 将作为对应点g的系统状态变量的两个分项。

设有向路段l的起点为g，终点为h。起点的 $n_{g,V,1}\left(k\right)$ 作为该路段起点的引力质量。而在 $kT+{\bar{t}}_l$ 时刻，完成可能司成匹配后的 $n_{h,P}\left(k+{\bar{t}}_l/T\right)$ 作为该路段终点的引力质量。定义有向路段l在给定的控制时间点kT的引力 $f_l\left(k\right)$ 如下：

$f_l\left(k\right)=\Psi \frac{{\left[n_{g,V,1}\left(k\right)\right]}^{\alpha }{\left[n_{h,P}\left(k+{\bar{t}}_l/T\right)\right]}^{\beta }}{d_l^2}$ . (1)

式(1)中的 $\Psi$ 、 $\alpha$ 和 $\beta$ 均为给定的正参数。我们选择 $f_l\left(k\right)$ 作为对应有向路段l的系统状态变量分项。

一辆空驶的出租车也可能选择当前的节点作停留，等待可能新出现的服务需求。因此类似于公式(1)，我们定义当前节点g的引力如下：

$f_g\left(k\right)=\Psi \frac{{\left[n_{g,V,1}\left(k\right)\right]}^{\alpha }{\left[n_{g,P}\left(k+1\right)\right]}^{\beta }}{d_T^2}$ , (2)

式(2)中， $d_T$ 表示出租车按照平均巡游速度在单位控制时间段T的行驶距离。节点的引力 $f_g\left(k\right)$ 将作为对应点g的系统状态变量的一个分项。

将所有网络节点上的 $n_{g,V,1}\left(k\right)$ 、 $n_{g,P}\left(k\right)$ 和 $f_g\left(k\right)$ ， $\forall g\in G$ 和所有路段上的 $f_l\left(k\right)$ ， $\forall l\in L$ 按照一定顺序组成向量 $s\left(k\right)$ 。为表述简洁， $s\left(k\right)$ 也被简写为 $s_k$ 。 $s\left(k\right)$ 就是对应控制阶段k的系统状态变量。所有可行系统状态变量值构成系统状态空间集合S。

3.4. 控制策略

增强学习理论中，控制策略指的是由一个给定系统状态变量决定一个控制行为的函数。 $\pi \in \Pi$ 表示一个控制策略， $\Pi$ 为所有可行策略集合。控制策略的函数形式可表示为：

$a=A^{\pi }\left(s\right)$ . (3)

增强学习模型的目的之一就是针对给定系统确定可达到某种优化目标的最佳策略。

3.5. 行为收益和状态价值

控制行为一旦选定，将会影响系统当前和随后的运行表现和后续决策。在增强学习理论中，一般将控制行为对系统当前运行的直接影响定义为控制行为的收益。

假设当前控制时刻为kT，节点g处的一辆空驶出租车 $v\in V_g^1\left(k\right)$ 选择节点 $h\in {\bar{G}}_g$ 作为其巡游的下一个目的地。为表述方便，当路段l以g为起点而以h为终点时，其引力满足 $f_{\left(g,h\right)}\left(k\right)=f_l\left(k\right)$ 。而当g和h为同一节点时， $f_{\left(g,h\right)}\left(k\right)$ 表示节点引力 $f_g\left(k\right)$ 。令 ${\bar{f}}_g\left(k\right):=ma{x}_{h\in {\bar{G}}_g}\left\{f_{\left(g,h\right)}\left(k\right)\right\}$ 。我们定义 $b_{g,h}^v\left(k\right):=f_{\left(g,h\right)}\left(k\right)/{\bar{f}}_g\left(k\right)$ 为对应上述目的地选择行为的收益。

对应系统状态变量 $s_k$ 和控制行为 $a_k$ 的控制行为收益函数定义为：

$b\left(s_k,a_k,{\Delta }_{k+1}\right)=\left[{\displaystyle {\sum }_{v\in V\left(k\right)}{b}_{g,h}^v\left(k\right)}\right]/n_{V\left(k\right)}$ . (4)

式(4)中的 $\Delta \left(k+1\right)$ 表示从阶段k到阶段 $k+1$ 系统演变过程中可变为已知的随机控制信息。 $n_{V\left(k\right)}$ 表示集合 $V\left(k\right):=\left\{v|v\in V,{\eta }_v\left(k\right)=0\right\}$ 中空驶出租车的数目。

合理的调度控制必须考虑控制行为对出租车服务系统后续表现的影响，以及这种影响的时间衰减性。因此我们选取如下的优化目标：

. (5)

式(5)中， $\gamma <1$ 为折扣因子，算子表示求变量的期望值。式(5)的优化目标为通过对空驶车辆巡游路线的调整，最大化控制期KT内阶段性控制行为收益的加权和的期望。

直接求解上述随机优化问题(5)非常困难，因此我们通常将其转化为等价的Bellman方程后再进行求解。设系统处于状态s时的状态价值为 $V\left(s\right)$ 。依据Bellman方程，最优状态价值 $V^{*}\left(s\right)$ 应满足：

$V^{*}\left(s_k\right)=\mathbb{E}\left[-b\left(s_k,A^{*}\left(s_k\right),{\Delta }_{k+1}\right)+\gamma V^{*}\left(s_{k+1}|s_k,A^{*}\left(s_k\right),{\Delta }_{k+1}\right)\right]$ . (6)

由式(4)和(5)可知，状态价值 $V\left(s\right)$ 的含义为：考虑时间衰减因素时，以s作为起始系统状态时系统在随后的运行过程中可以得到的总的期望收益的相反数。

下节将设计对应的Q学习算法求解方程(6)。 $V\left(s\right)$ 与Q函数 $Q\left(s,a\right)$ 具有如下关系：

$V\left(s\right)=\underset{a}{\max }Q\left(s,a\right)$ . (7)

与 $V\left(s\right)$ 相比， $Q\left(s,a\right)$ 的变量维度增加了一位；但是实际应用时可通过比较不同控制行为的 $Q\left(s,a\right)$ 值更方便地确定最佳控制行为。由于 $Q\left(s,a\right)$ 的具体形式未知，因此需要利用某种带有待定参数 $\theta$ 的近似函数 $Q\left(s,a\text{,}\theta \right)$ 来替代 $Q\left(s,a\right)$ 实现问题的求解。

4. 求解算法

下面将介绍求解问题(6)的Q学习算法。该方法中的Q函数为人工神经网络(ANN)近似函数，具有待定参数 $\theta$ 。算法中k代表当前阶段的序列号。m表示对系统进行仿真模拟的序号。K和M分别是总的阶段数目和模拟仿真总次数。针对出租车调度优化的Q算法的求解步骤如下：

步骤1：初始化。

步骤1.1. 对所有的系统状态 $s\left(k\right)$ ，给出价值函数 ${\bar{Q}}_k^0\left(s_k,a_k,\theta \right)$ 的近似值以及控制行为 $a\left(k\right)\in A\left(k\right)$ ， $k=\left\{0,1,\cdots ,K-1\right\}$ 。其中 $\theta$ 的初始值从区间 $\left[0,\text{1}\right]$ 中随机生成。

步骤1.2. 令 $m=1$ 。

步骤1.3. 初始化 $s^1\left(k\right)$ 。

步骤2：选择一个随机信息的样本路径 ${\omega }^m$ 。

步骤3：将下面操作步骤依 $k=0,1,\cdots ,K-1$ 加以循环迭代：

步骤3.1. 利用 $\epsilon$ 贪婪规则确定控制行为。以概率 $\epsilon$ ，从控制行为集 $A\left(k\right)$ 中随机选择行为 $a_k^m$ 。而以概率 $1-\epsilon$ ，利用公式 $a_k^m\in \underset{a_k\in A\left(k\right)}{\arg \max }{\bar{Q}}_k^{m-1}\left(s_k^m,a_k,\theta \right)$ 选择行为 $a_k^m$ 。

步骤3.2. 对信息 ${\Delta }_{k+1}^m=\Delta \left({\omega }^m\left(k+1\right)\right)$ 进行取样，并计算下一阶段的状态变量 $s_{k+1}^m=S^{\Gamma }\left(s_k^m,a_k^m,{\Delta }_{k+1}^m\right)$ 。 $S^{\Gamma }(\cdot )$ 为系统状态转移函数，表示系统演进到下一控制状态。

步骤3.3. 计算 ${\hat{q}}_k^m=-b\left(s_k^m,a_k^m,{\Delta }_{k+1}\right)+\gamma \underset{a_{k+1}\in A\left(k+1\right)}{\max }{\bar{Q}}_{k+1}^{m-1}\left(s_{k+1}^m,a_{k+1},\theta \right)$ 。

步骤3.4. 更新 ${\bar{Q}}_k^m$ 和 $\theta$ 。

首先，依据下式对 $\theta$ 进行更新：

$\theta :=\theta +\lambda \nabla {\bar{Q}}_k^{m-1}\left(s_k^m,a_k^m,\theta \right)\left({\hat{q}}_k^m-{\bar{Q}}_k^{m-1}\left(s_k^m,a_k^m,\theta \right)\right)$ 。

其次，基于更新后的参数 $\theta$ ，对Q因子进行如下更新：

${\bar{Q}}_k^m\left(s_k^m,a_k^m\right)=\left(1-{\alpha }_{m-1}\right){\bar{Q}}_k^{m-1}\left(s_k^m,a_k^m,\theta \right)+{\alpha }_{m-1}{\hat{q}}_k^m$ 。

步骤4：令 $m:=m+1$ 。如果 $m\le M$ ，转步骤2。

步骤5：给出最终的Q因子 ${\left({\bar{Q}}_k^M\right)}_{k=1}^{K-1}$ 和 $\theta$ 。

$\nabla {\bar{Q}}_k^{m-1}\left(s_k^m,a_k^m,\theta \right)\left({\hat{q}}_k^m-{\bar{Q}}_k^{m-1}\left(s_k^m,a_k^m,\theta \right)\right)$ 可看作函数 $z\left(\theta \right)=\left(1/2\right){\left({\hat{q}}_k^m-{\bar{Q}}_k^{m-1}\left(s_k^m,a_k^m,\theta \right)\right)}^2$ 的负梯度方向。这里 $\theta$ 作为自变量，而 ${\hat{q}}_k^m$ 为给定值。那么上述算法可以看作是在求解 $z\left(\theta \right)$ 的最小值。依据经典非线性规划理论，如果当前 $\theta$ 对应的函数值非局部或全局最小值，且步长足够小，目标函数 $z\left(\theta \right)$ 的值将沿当前变量 $\theta$ 处的负梯度方向下降。因此算法中的参数 $\lambda$ 相当于沿可行下降方向的搜索步长。

5. 算例分析

考虑图1所示的出租车服务运行网络。路段的标号已在图中标出，路段标号后括号内的数字表示该路段的长度(km)。假设连接两个节点的两条相反方向的路段长度相等。假设出租车在所有路段上的平均巡游速度均为10 m/s (36 km/hr)。由各路段长度除以该平均速度即可得到每条路段的平均行程时间。例如路段4的平均行程时间为2500 (m)/10 (m/s) = 250 (s)。通过路段l的行程时间误差 ${\epsilon }_l$ 服从正态分布 $N\left(0,5d_l\right)$ ，其中 $d_l$ 为路段l的公里数。

Figure 1. The operation network of taxi service

图1. 出租车服务运行网络

Table 1. The generation rate of passengers r g and the gathering coefficient ϖ g

表1. 节点的乘客生成率 $r_g$ 和乘客集聚系数 ${\varpi }_g$

表1给出了节点的乘客生成率 $r_g$ 和乘客集聚系数 ${\varpi }_g$ 。此表中 $r_g$ 的单位为(乘客数/分钟)。这里乘客集聚系数可以理解为该节点作为出租车乘客目的地的相对吸引力，无量纲。利用乘客集聚系数 ${\varpi }_g$ 可以通过下面的式(8)和式(9)得到乘客的目的地选择概率 $r_{g,h}$ ：

$r_{g,h}=\left({\varpi }_h/{\bar{t}}_{g,h}\right)/\left[{\displaystyle {\sum }_{j\in G/\left\{g\right\}}\left({\varpi }_j/{\bar{t}}_{g,j}\right)}\right]$ , $\forall h\in G/\left\{g\right\}$ , (8)

$r_{g,g}=0$ . (9)

网络中共有20辆出租车。在调度开始时。出租车均为空驶状态，且随机分布在7个节点处。设总的时间分段数K为100，总的仿真次数M为300，参数 $\epsilon$ 和折扣因子 $\gamma$ 均设为0.5，算法步长 $\lambda$ 设为0.05。引力公式(1)和(2)中的参数 $\alpha$ 和 $\beta$ 取值均为1，参数 $\Psi$ 取值为100。其他的系统参数为 $T=100\text{s}$ 、 $c_0=14元$ 、 $\stackrel{\rightharpoonup }{c}=\text{2}.\text{5}元$ 、 $d_0=\text{3}\text{km}$ 和 $\stackrel{⌢}{t}=\text{4}00\text{s}$ 。

表2中给出了控制与无控制情景下常见的出租车服务水平度量指标，包括出租车总的空驶里程(Total travel Distance of Vacant taxis-TDV)、总的司乘匹配数(Number of passenger and taxi Matching Pairs-NMP)、总的出租车运营收入(Total Income of Operation of taxis-TIO)、未得到服务而损失的乘客数(Un-Served Passenger-USP)以及一次仿真过程中所有控制行为的总控制收益(Total Benefit-TB)。表中数据表明服务水平指标在调度优化控制条件下均有明显的改善。因为系统本身的随机特征，上述数据和随后给出的数据均为系统经过一次仿真或多次仿真得到的代表性结果。

Table 2. The comparison of measure indexes of service level

表2. 出租车服务水平度量指标比较

在图2、图3和图4中，我们分别给出了总的控制收益(TB)、总的空驶里程(TDV)以及总的出租车运营收入(TIO)随仿真次数增加的变化情况。尽管上述三个指标由于系统本身随机特性而具有强烈的波动特征，但是三个指标的总体变化趋势均呈现提升特征。总控制收益(TB)和总运营收入(TIO)表现出上升趋势，而总空驶里程(TDV)表现出下降趋势。

Figure 2. The change trend of TB

图2. 仿真中总的控制收益(TB)变化

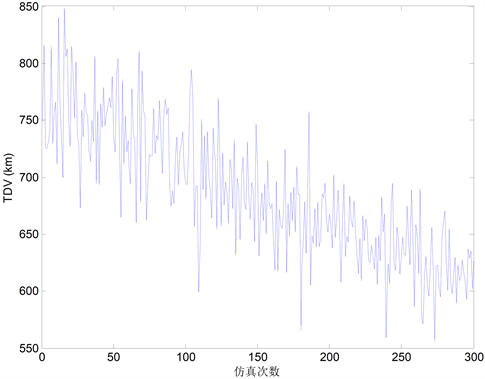
Figure 3. The change trend of TDV

图3. 出租车总的空驶里程(TDV)变化

Figure 4. The change trend of TIO

图4. 总的出租车运营收入(TIO)变化

图5给出了总的司乘匹配数(NMP)和未得到服务损失乘客数(USP)随仿真次数增加的变化趋势。总的司乘匹配数(NMP)呈现上升趋势，而未得到服务损失乘客数(USP)呈现下降趋势。值得注意的是给定仿真下两者和的均值为528.6567，上下变化的区间为[470, 590]。由表2中的乘客生成率 $r_g$ (乘客数/分钟)，可知 ${\displaystyle {\sum }_g\left(r_g/60\right)}$ 为系统一秒钟内生成的乘客数均值。而总的控制时长为KT (秒)，因此在控制时长内生成的期望乘客数为 $KT{\displaystyle {\sum }_g\left(r_g/60\right)}\approx 533$ 。该期望乘客数与300次仿真中生成的乘客均值一致。

算例求解的计算机程序用Java 1.8.0编写，在NetBeans IDE 8.0.2开发环境下实现，所用计算机处理器为Intel® Core i3-3120M CPU。调度控制方式下完成300次系统仿真的计算时间约为8 s，而完成一次仿真的计算时间变化范围为[0.014 s, 0.032 s]。

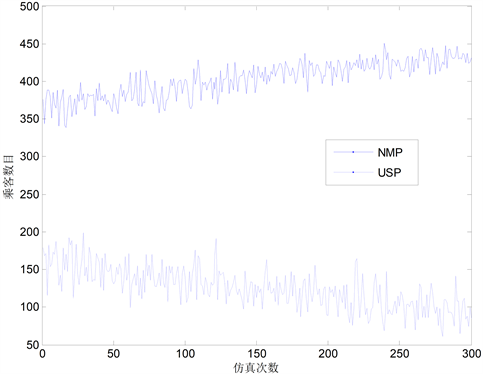
Figure 5. The change trends of NMP and USP

图5. 总的司乘匹配数(NMP)和未得到服务损失乘客数(USP)的变化

6. 结论

通过类比万有引力定理，将出租车的揽客行为加以建模，并从时空演化的角度引入增强学习理论，从而实现城市规模的区块化出租车动态调度与空驶路线调整。研究表明：为增加揽客成功的机率，不仅需要考虑预期的目的地等车乘客数量，也需考虑到达该目的地的行程距离带来的不确定性风险；出发点空驶出租车数辆，也可对司乘的最终匹配结果产生影响；优化后，出租车总的空驶里程和总的运营收入都有显著增加，总的司乘匹配数也有所增加，而未得到服务损失乘客数有所下降。

基金项目

国家自然基金项目(71601118，71801153，71871144)；上海市自然科学基金项目(18ZR1426200)。

NOTES

^*通讯作者。