1. 引言
隧道的密闭化、地下化的特点使得隧道内一旦发生事故,将给救援带来极大的困难,同时对驾驶人心理也将产生一定的影响,造成隧道内交通拥堵,甚至引发二次事故。由此,事故发生的第一时间给出最优应急疏散方案,尽快救援隧道内受伤人员,疏散隧道内拥堵的车流变得尤为重要。国内外对城市隧道应急疏散研究的较少,而对公路隧道的研究开始的最早,更多的成果主要集中在公路隧道上。而城市隧道兼具公路隧道与城市道路的特点,公路隧道应急疏散策略相关研究成果可以作为参考。
国内外学者普遍从隧道事故影响以及隧道疏散组织策略两大方面进行研究。在隧道事故影响方面,主要从事故影响持续时间预测以及排队长度预测两方面着手。如Ahmad Tavassoli Hojati [1] 采用风险分析法,考虑了与各种交通事故类型持续时间有关的因素,建立了生存参数加速失效的预测模型。Li R [2] 基于加速失效时间风险模型,建立城市快速路交通事件分阶段的持续时间预测模型,并考虑了未观测的异质性、时变的相关变量和连续交通事件持续时间之间的关系。黄亚龙 [3] 用回归分析法和决策树模型对隧道事故持续时间进行了详细研究,孙明玲等 [4] 分析了交通事故前后车流波及拥挤排队长度的变化,以及分流波对车辆疏散的影响。
而对于城市隧道应急疏散组织策略研究方面,一些学者应用交通波理论进行研究,如谢雅丽 [5] 通过分段停车控制有效地缩短了车辆停车排队长度,胡文娟 [6] 则提出三级分流控制模式,最终实现疏散效率最大化的目标。另一些学者则从控制策略处着手,进行隧道应急疏散,如陈瑜 [7] 针对事故主要成因进行合理限速和设置交通标志的方法有效地完成了交通事故的应急疏散,并评价事故影响区域交通组织方案的实施效果。Daniel Alvear等人 [8] 基于Lantueno隧道提出一种用于隧道应急管理的快速决策系统,在基于对隧道内发生交通事故的严重程度、事故持续时间以及事故疏散时间的判断,做出相应的隧道应急管理决策,并进行了模拟测试。周昱 [9] 构建了基于贝叶斯网的高速公路隧道安全预测模型,对隧道交通安全事故进行定量的预测分析,同时提出相应的隧道应急策略。
综上,国内外学者对公路隧道应急疏散做了大量的研究,而对城市隧道的研究明显不足。由于城市隧道与公路隧道在路网结构中对其他道路的影响不同、在交通运行上车型比例的不同、同等长度中所包含的车辆数的不同,则应急疏散策略必定有其自各的特点与规律。
本文以城市隧道作为研究对象,考虑到城市隧道对城市其他道路的影响,摈弃了公路隧道选用疏散策略时所依据的事故严重程度这一指标,而是以持续时间和排队长度作为评价指标确定事故影响程度的等级,制定针对不同等级下的应急疏散预案,使得城市隧道在选用应急疏散策略时更有针对性。经过VISSIM仿真软件仿真模拟的结果可知,明显提升了应急疏散的效率。
2. 隧道事故影响程度分析
2.1. 事故影响持续时间
事故影响持续时间如图1所示,可分为四个阶段:事故发现时间、事故响应时间、事故清除时间以及交通恢复时间。

Figure 1. Four stages of accident duration
图1. 事故持续时间四阶段
目前交通事故影响持续时间预测模型主要有决策树模型、概率分布、风险分析模型、层次分析模型、回归分析模型以及时间序列模型。回归分析模型是对不同的影响因素采用回归分析法进行数据处理,由此而得出对事故持续时间影响最为明显的因素,再根据所获得的明显因素组合建立多元线性回归方程。由于城市隧道交通事故数据较难获取,因此,本文借鉴刘伟铭等 [10] 人对公路隧道交通事故数据的研究成果进行分析。刘伟铭等人通过研究830组可用的事件数据,利用逐步回归分析的方法,得出8个显著影响因素,并建立了事故持续时间的多元线性方程:
(1)
式中:x1——卡车数;x2——翻车;x3——位置;x4——路产损坏;x5——交通阻塞;x6——死亡人数;x7——重伤人数;x8——危险材料。
根据表1对多元线性回归方程中的因素变量进行取值:
从上面的方程式中可以看出:在这八个显著影响因素中,危险材料对事故持续时间的影响最大,若发生交通事故的车辆载有危险材料,则事故持续时间增加约58.7 min。若事故中发生车辆翻车及出现人员死亡,将会使隧道事故持续时间大大增加,翻车使事故持续时间增加19.4 min,死亡人数使事故持续时间增加26.4 min。对于城市隧道,由于对卡车及危化品车辆限行,并且城市隧道限速值低于公路隧道,且城市隧道路况较好,鲜有路产损坏现象,因此城市隧道出现翻车的概率极低,不予考虑。可以得出城市隧道事故影响持续时间影响因素主要是交通量、死亡人数、重伤人数。

Table 1. Comparison of factors affecting the duration of accidents
表1. 事故持续时间影响因素取值对照表
2.2. 排队长度
交通事故必然会影响隧道路段的交通流。在事故路段处,由于车道被事故车辆占用,从而形成瓶颈路段,降低了道路的通行能力。事故发生后,交通流密度在事故点处瞬间变大后形成拥堵。故此,事故排队长度的有效预测将有助于管理部门预知事故影响范围,进而制定合理的应急疏散方案。
交通波理论是运用流体力学的基本原理来对交通现象进行分析。本文采用交通波模型来对事故发生后的排队长度进行预测。
假定某城市隧道内发生交通事故,则在没有进行疏散前交通事故的排队长度模型为:
(2)
式中:L——没有疏散前的排队长度;QL——道路最大通行能力;Qf——事故后道路的通行能力;Qa——上游车辆到达事故点的交通量;V——事故前车辆正常的行驶速度;t0——事故影响持续时间。
在事故点未清理完成前,进行分流疏散管理。在te时刻距离事故点le处,即车行横通道位置处进行分流,分流流量为Qe。
那么进行分流管理措施后,排队长度预测模型为:
(3)
到达最大排队长度的时刻为:
(4)
进行分流疏散后排队所需要的最小消散时间为:
(5)
从以上建立的交通事故排队长度预测模型可以看出,排队长队主要与交通量、通行能力以及事故持续时间相关。其中,事故影响持续时间越长,交通量越大,那么事故引起的排队长度也就越长。
3. 城市隧道交通事故应急预案
3.1. 事故影响等级划分
公路隧道发生交通事故后,相关应急管理部门会在第一时间对事故等级进行初步判断,然后依照事故等级对应的预案进行应急疏散。由于对公路隧道研究较早且相对成熟,且城市隧道与公路隧道有许多相似之处,因此,城市隧道交通事故应急疏散预案也多根据交通事故等级确定。隧道交通事故分级表如表2所示。

Table 2. Tunnel traffic accident rating table
表2. 隧道交通事故分级表
然而,由于城市隧道包含于城市道路网络中,绝大多数城市隧道禁止危化品车辆驶入,且相比于公路隧道,城市隧道与周边路网联系更加紧密,可以说城市隧道应急疏散策略更多的是与交通事故的影响程度有关,并非取决于事故的严重等级。因此,由式(2)至式(5)对城市隧道交通事故发生后预测的影响持续时间和预测的排队长度作为应急疏散等级确定的依据,如表3所示。

Table 3. Comparison of emergency evacuation levels of urban tunnel traffic accidents
表3. 城市隧道交通事故应急疏散等级对照表
在表3中,t为预测持续时间,L为预测排队长度,ta,tb分别为判别应急疏散各等级划分的持续时间阈值;La,Lb分别为判别应急疏散各等级划分的排队长度阈值。当持续时间与排队长度对应急疏散等级判定不一致时,取等级较高的级别。ta,tb,La,Lb由当地交通管理部门根据隧道的长度及施设情况进行确定。
3.2. 隧道区段划分
以南京市长江隧道为例,对隧道内发生交通事故进行应急疏散策略说明。南京长江隧道总长度5853 m,设计为双向六车道,限速80 km/h,车道宽度为3.5 × 2 + 3.75 m,车道净高4.5 m。隧道内车行横通道为三个,人行横通道为4个。通过对隧道进行分区来针对发生在隧道不同区段的事故进行疏散策略分析。根据隧道内车行横通道的位置对隧道进行分区,长江隧道河西新城区–梅子洲–浦口区路线共有三个车行横通道,因此将隧道划分为8个区域,如图2所示。

Figure 2. Schematic diagram of area division
图2. 区域划分示意图
3.3. 交通事故应急疏散预案
以B区发生严重等级这一种情况进行详细说明,如图3所示,其他情况以此作为参照。
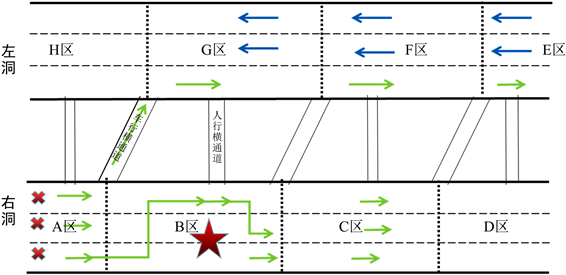
Figure 3. Schematic diagram of accident evacuation in Zone B
图3. B区内发生事故疏散示意图
如图3所示,当隧道B区发生交通事故造成严重影响等级时,应急疏散预案步骤如下:
1) 出警,对左右洞隧道入口上游进行交通管制。
2) 指挥平台利用电子设备封闭隧道入口。右洞隧道入口上游的可变信息标志牌显示“隧道封闭,请绕行”。右洞入口处三个车道均显示 ,封闭隧道。左洞隧道入口上游的可变信息标志牌显示“隧道左侧车道封闭,请勿驶入”。左洞入口处最内侧车道显示
,封闭隧道。左洞隧道入口上游的可变信息标志牌显示“隧道左侧车道封闭,请勿驶入”。左洞入口处最内侧车道显示 ,封闭左侧车道。
,封闭左侧车道。
3) 指挥平台利用隧道内电子设备对隧道交通进行组织。左洞隧道内左侧车道可变信息牌显示 ,提醒左侧车道车辆进行变道。左洞隧道全程限速“40 km/h”。右洞隧道内事故发生点上游的可变限速标志变为“40 km/h”,且车道控制标牌显示“
,提醒左侧车道车辆进行变道。左洞隧道全程限速“40 km/h”。右洞隧道内事故发生点上游的可变限速标志变为“40 km/h”,且车道控制标牌显示“ ”,提醒车辆变道行驶,汇入内车道行驶。待隧道左洞左侧车道车辆清空后,临时更改为逆向车道,供右洞车辆行驶。事故发生点下游的交通信号灯显示为绿色“
”,提醒车辆变道行驶,汇入内车道行驶。待隧道左洞左侧车道车辆清空后,临时更改为逆向车道,供右洞车辆行驶。事故发生点下游的交通信号灯显示为绿色“ ”,车辆继续正常通行,直至离开隧道。事故持续过程中,使用隧道内广播,告知隧道内驾驶员隧道出现交通事故,减速慢行,注意变更车道,并反复提醒左洞隧道左侧车道驾驶人进行车道变更。
”,车辆继续正常通行,直至离开隧道。事故持续过程中,使用隧道内广播,告知隧道内驾驶员隧道出现交通事故,减速慢行,注意变更车道,并反复提醒左洞隧道左侧车道驾驶人进行车道变更。
4) 地面交警第一时间进入隧道进行现场交通组织,待隧道内交通疏散后,对交通事故进行处理,清除道路上的障碍物后,恢复隧道通车。
4. 仿真分析
本文以VISSIM建立城市隧道运行模型来模拟交通事故下的疏散策略。在交通事故发生的前提下,分别对无策略及有策略疏散的两种情况进行模拟,得到其行车延误时间以及排队长度。本次模拟输入交通量为2500 veh,事故持续时间预测为35 min,事故发生在第5 min。
当事故发生在B区段,不实施应急疏散策略,车辆遇到事故点自由避让后继续向前行驶,则VISSIM仿真如图4所示。
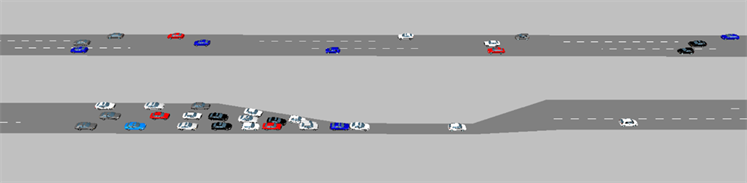
Figure 4. Vehicle running simulation without strategy
图4. 无策略下车辆运行
当事故发生在B区段,实施应急疏散策略,右洞隧道左侧车道车辆可通过车行横通道借用左洞隧道左侧车道行驶,刚VISSIM仿真如图5所示。
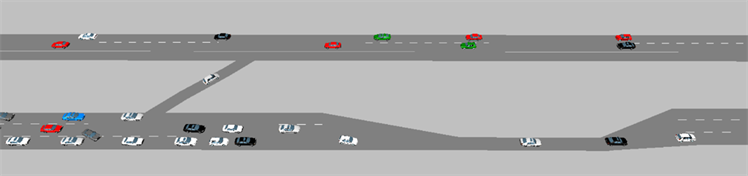
Figure 5. Vehicle running under strategy
图5. 有策略下车辆运行
根据VISSIM仿真模拟事故,对无管控车辆运行以及合理疏散方案运行下排队长度随时间的变化曲线进行对比,如图6所示:

Figure 6. Comparison of non-strategic and strategic queuing lengths over time
图6. 无策略与有策略排队长度随时间对比图
从图6中可以看出:由于需要事故反应时间,当事故发生时,一开始两种情况的排队状况基本一致。而当开始进行交通管制时,事故上游车辆会根据隧道内交通指示,经车行横通道借用左洞隧道左侧车道行驶。排队长度增加趋势明显变缓,且远小于无策略下的排队长度。最大时,两者排队长度相差250多米。影响持续时间也减少了2分钟。由于事故发生在距隧道入口处较近的B区段,需要应急疏散的车辆较少,因此影响持续时间减少的不明显,如果事故发生在隧道的中、下游,则有、无应急策略的差别将更为明显。由此可知,合理的疏散策略有助于降低车辆的延误时间,减少排队长度,从而降低交通事故对隧道路网的影响。
5. 结论
对城市隧道应急疏散策略进行研究,得到以下结论:
1) 当前对城市隧道应急疏散等级的确定仍使用公路隧道的相关标准,由于城市隧道不允许危化品车辆驶入,因此城市隧道与公路隧道在事故严重程度方面有很大差异。以交通事故影响程度作为确定城市隧道应急疏散等级的依据更符合城市隧道管理的实际情况。
2) 以城市隧道两个方向间的车行横通道对隧道划分区段,针对交通事故发生所处的区段实施应急疏散策略,相比于无策略而言,交通疏散的效果显著。
3) 限于数据难以获得,仅从理论上进行研究分析。
基金项目
南京工业大学青年教师科研启动基金(3827400205)。