1. 引言
胞腔代数的出现完满地解答了表示论中的一个最基本的问题——确定不可约表示的参数集。Kazhdan-Lusztig在文献 [1] 中研究Hecke代数的表示理论时,引入了Kazhdan-Lusztig基,通过这组基,他们确定了不可约表示和一些相关问题。受到A-型Hecke代数这组基的乘法性质的启发,Graham和Lehrer在文献 [2] 中首次引入了胞腔代数的概念;Xi和König在文献 [3] 中给出了胞腔代数的一种全新等价定义,即胞腔代数A将会有一个R-模分解,并且将会根据这个R-模分解来构造出一条胞腔理想链,同理,如果能够在代数A上构造出一条胞腔理想链,那么这个代数就是一个胞腔代数。通过胞腔理想链,可以更好地研究和理解胞腔代数的结构和同调性质。由于胞腔理想链也是双边理想链,因此研究双边理想链有助于研究代数的胞腔性。正则半群是一类重要的半群,它构成了半群代数理论的主要研究领域之一。因此本文将对正则半群代数的双边理想链进行研究,探索该双边理想链与某些极大子群的群代数的胞腔理想链之间的关系。
2. 预备知识
在这一节中,我们给出本文需要得一些关于半群和胞腔代数的基本概念和定义。本文的R将表示一个具有单位元的交换环,
将表示理想
的生成元,并且把代数A的R-线性反自同构
叫做R-对合。本节未提及的概念和定义请见参考文献 [4] [5]。
我们首先回顾一下关于半群的一些定义和结论。
设S是一个半群,
是S的全部幂等元所组成的集合,如果半群S没有单位元,则用
表示半群S并上一个单位元,否则,
。S上的格林关系 [6]
和
在半群理论中起着十分重要的作用,对于
,有:
当S是一个有限半群时,格林关系
。设
是S的格林关系之一,取
为S的
-类并且包括a,
为S的全部的
类所组成的集合。我们定义:
因此,可得集合
、
和
上的偏序集。
设S是一个半群,如果对任意的
,存在
,
且
,则称S为正则半群。
设S是一个含有零元的半群,如果对任意
,有
,那么称半群S为完全0-单半群。
设G是一个群,Ι和
是非空的集合,
是
上的一个正则
矩阵,其中P的每一行和每一列都至少包含G中的一个元素。设
,定义S上的乘法,任意
,
,
,有:
并且
。如上定义的S是一个完全 0-单半群,我们将用
来表示。在
中,我们可以假设
,
,
,其中e是G的单位元。此外对于
的任意非零极大子群
,我们有
。本文的
总是满足上述假设。
设S是一个含有零元的半群且
。令
,
,则在
上定义运算
,任意
:
其中xy是x和y在S上的乘积。显然,
是一个具有零元0的半群。称
为S的由a决定的主因子。注意到,有限正则半群S的每一个主因子都是一个完全0-单半群。
任意
,则
是
的一个理想,显然,
。
如果
是一个具有零元
的半群,
是域R上的向量空间,并且对于任意
,
,有
,则
是半群代数。定义
。我们称R-代数
是R上的S的压缩半群代数。若S没有零元,则
。设
,即
。定义a的支撑集合:
。
引理2.1 [7]
设S是一个半群:
1) 若
,则
或
。同理,
或
;
2) 取
。若
,则
。同理,若
,则
。
引理2.2 [7]
任意
,有如下三个等价论述:
1)
;
2)
;
3)
。
定义2.3 [3]
设A是一个具有单位元的R-代数,这里的R是一个Noether整环,设
是A上的R-对合,J是A的一个理想。若J是一个胞腔理想,则它满足:
1)
,即对任意的
都有
;
2) 存在A的一个左理想
,它是有限秩的自由R-模,以及一个A-A-同构
,使得下图交换:
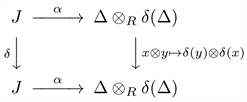
定义2.4 [3]
设A是一个R-代数,且
是A上的一个对合。则A称为胞腔代数,如果存在A的一个R-模分解
(有限直和)满足:
1) 对任意的j,
;
2) 令
,则:
是A的一个理想链,使得对于每个
,
是商代数
的一个胞腔理想(其中
上的R-对合是由
诱导的)。这时,称这个理想链为A的一个胞腔理想链。
引理2.5 [8]
设
是一个完全0-单半群,e是G的单位元,R是一个整环,且
是
的
型对合。若
,则存在
上的一个对合
,以及一个双射
,
。
定义2.6
设S是一个半群,称半群代数
是一个
型胞腔代数,如果
是一个胞腔代数,且满足下面的条件,对于任意
,有:
1)
;
2) 其中
是
的左理想,并且满足
,J为S的某个
-类,J可能依赖于给出的k。此时,称
的胞腔理想链为
型胞腔理想链。
定义2.7
设S是一个半群,则半群代数
是一个
型胞腔代数,如果
是一个
型胞腔代数,且满足条件,对于每一个k和
,存在一个S的
-类H,使得
。此时,称
的胞腔理想链为
型胞腔理想链。
定义2.8
设
是半群代数
上的一个R-对合,则:
1) 对于每一个
,有
,则
是一个
型对合;
2) 对于每一个
,任意
,将存在一个S的
-类H,使得
,则
是一个
型对合。
3. 主要定理
定理3.1
设S是一个半群且
是
上的一个对合,若
关于对合
是一个
型胞腔代数,则对合
是一个
型对合。
证 因为
是一个
型胞腔代数,所以
具有一条
型胞腔理想链:
。
设
。因为
型胞腔理想链的定义,对任意的
和
,都存在S的一个
-类J,使得
。取:
。
下面要证明对合
是一个
型对合,也就是对任意
,有
。由于S的不同的
-类是不相交的,则
是
的一组基。对于任意的
,有:
。(1)
因为
,所以s可以由
中的元素张成。再结合(1),就可以得到
。故对合
是一个
型对合。
定理3.2
设
是一个完全 0-单半群,e是G的单位元,
是
上的对合,且
,假设
,那么映射
,
,其中
,
。则
是一个
型对合。
证显然
可线性扩展到
,任意
,有:
。
因此
。
再取
,则有:
。
此处我们认为G等同于S的子群
。因此
是一个R-对合。又因为对于每一个
,任意
,我们从引理2.2中可以知道,都将会存在一个S的
-类H,使得
,最后根据定义2.8可知,
是一个
型对合。
定理3.3
设S是一个半群,
是
上的一个R-对合,如果
关于
是一个
型胞腔代数,那么对于每一个
,R-代数
都会有一条双边理想链。
证由于
是
型胞腔代数,因此取
的
型胞腔理想链如下:
。
设
,
具有R-模分解:
,
,
,
并且
是
的胞腔理想,因此存在
上的同构映射
,存在
上的左理想
,使得:
。
设
。根据定义2.6可知,任意
,
,都有
。注意,
中元素的先后顺序与I中元素的先后顺序保持一致,为了方便叙述,定义
。为了证明
具有一条双边理想链,我们只需要证明如下两个问题:
1)
显然,集合:
构成了
的一组 R-基,因此对于任意
,我们有:
,
其中
。由于
是
型胞腔代数,因此有:
,
所以可得:
,
因此我们有
。又由于任意
,都有
。因此
,证得:
。
2) 取
,并且
是
的双边理想链。
先取任意
,
,显然有
。又因为当
,
时,我们有:
和
。
因此可得如下等式:
又由于式子
,因此:
。
同理,我们也可以证明
。因此
是
的双边理想链。
定理3.4
设R是一个整环,S是一个完全0-单半群,
是
上的一个
型对合。
,
,若
,
是S关于单位元e的极大子群,如果
关于R-对合
是一个
型的胞腔代数,则
有一条双边理想链,相反,如果
关于R-对合
是一个胞腔代数,则
也有一条双边理想链。
证 由于
是
上的一个
型对合,因此我们可以假设
,并且
。
假设
是一个
型的胞腔代数,那么
会具有一条
型胞腔理想链:
。
设
,
具有R-模分解:
,
,
。
并且
是
的胞腔理想,因此存在
上的同构映射
和
上的左理想
,使得
。取:
。
设集合
是由集合:
中的元素R-线性生成的,取
。注意,
中元素的先后顺序与I中元素的先后顺序保持一致,为了方便陈述,设
,为了证明
有双边理想链,我们只需要证明如下两个问题:
1)
先证
。
因为
,故存在
,使得
。又因为e是
的一个左单位元,故有:
。
对于任意
,
,我们有:
。
根据文献 [2] 的定义1.1的C3,显然可以推出系数
。又因为集合:
中的每一个元素的支撑都包括在一个
-类之中,所以上述等式右边的非零系数所对应元素的支撑一定包含在
中。故
。应用对合
,同理可得
。因此任意
,
,有:
。
可得
。
再证
。
取
,我们可以写成
,
,
。当
时,则有
,可得
。又因为
,故
。那么
,
。
因此问题(1)得证,
。
2) 设
,则
是
的一条双边理想链。
设
,
,由于
是
的双边理想,则有
是
的左理想,有:
。
当
,
时,我们有
和
。又由于
(2)
和
(3)
故式子(2)和(3)都为 。因此有:
。
同理可证,
。因此
是
的一条双边理想链。
相反,假设G的群代数
关于对合
是一个胞腔代数,则
存在一条胞腔理想链:
。
设
,
具有R-模分解:
,
,
。
并且
是
的胞腔理想,因此存在
上的同构映射
和
上的左理想
,使得
。
根据
是一个
型对合,因此我们可以假设
。根据定理3.2,我们还可以假设
。显然:
,
取
。故可得:
。
因为
是一个胞腔代数,取
,则任意
,
,有
,
。又因为
,
,故有
和
。
对于任意
,任意
,有
,又因为
,所以
。类似地,
,
,因此
。故
是
的双边理想。因此
有一条双边理想链:
。
定理3.5
设R是一个整环,S是一个正则半群(其主因子为
,
取遍
,Υ 有限)。假设
是一个
型和
型对合。在
上,设
。取
,设
是具有单位元e的S的极大子群。假设
,
。如果
关于对合
是一个
型的胞腔代数,则每一个
,都有
,使
有一条双边理想链,相反,若
关于对合
的限制是一个胞腔代数,则
也有一条双边理想链。
证假设
是一个
型的胞腔代数,通过文献 [8] 的命题5.1可知,任意
,
也是胞腔代数。取
,那么存在
。因此
是一个完全0-单半群,并且
。又由于
,则
是
在R上的半群代数。由于是在
型的条件之下,根据引理2.5,有
。又由于
,故存在幂等元
,并且
是关于单位元e的
的极大子群,则
,此外,我们还把e定义为
,易证
和
满足定理3.4的条件,因此
有一条双边理想链。
由于S是一个含有有限个
类的正则半群,因此它会存在一条满足相邻理想的商是主因子的理想链:
。
显然
也具有一条理想链:
。
其中
,有
,并且
。
由于每一个主因子
的R-代数
都是一个胞腔代数,设
的胞腔理想链为:
。
其中
,
。
根据理想链:
,
再作出一条新的链:
。
现在需要证明该链是一条双边理想链。
对于任意
,任意
,其中
,
。由于
是
的双边理想,因此
和
都属于
,取
,又由于
或者
,因此我们有如下两种情况:
1)
。
只需要证明
属于
即可。由于
,故
,因此可得:
。
又由于
,
,并且
是
的双边理想,故
。
2)
。
由于
是
的理想,则
。又由于
,因此也有
。并且
是
的双边理想,可得:
,
又根据
,可得
。则
,显然
。因此
也有一条双边理想链:
。
推论3.6
设R是一个整环,S是一个有限正则半群,
上的R-对合
既是
型又是
型,E是S的所有幂等元e所成的集合,其中
。对于每一个
,取
为关于单位元e的S的极大子群。如果对于任意
,
,那么
关于对合
是一个
型胞腔代数,则对于每一个
,群代数
都具有一条双边理想链,相反,若群代数
关于对合
的限制都是一个胞腔代数,则
将会具有一条与其相关的双边理想链。