上海市近二十年房价水平影响因素及发展趋势研究

Research on Influencing Factors and Development Trends of Housing Price Level in Shanghai in the Past Two Decades

摘要: 本文通过收集2000年2月至2021年4月上海市月度住房价格及相关解释变量，对上海市房价水平进行研究。报告首先建立了上海市房价水平与住房销售面积、住宅开发投资额、住宅施工面积、住宅竣工面积的多元线性回归模型并对模型进行了正态性检验和异方差性检验，发现存在异方差，利用加权最小二乘法(WLS)进行处理。接着将研究时间段人为划分为训练集和测试集，在训练集上建立房价水平的时间序列ARIMA模型，得出相关结论，并对住房价格宏观调控政策提出了建议。

Abstract: This paper collects monthly housing prices and related explanatory variables in Shanghai from February 2000 to April 2021 to study the level of housing prices in Shanghai. The report first established a multiple linear regression model between the level of housing prices in Shanghai and housing sales area, residential development investment, residential construction area, and residential completed area. The model was tested for normality and heteroscedasticity, and it was found that there was heteroscedasticity. Weighted Least Squares (WLS) was used for processing. Then the research time period is divided into training set and test set artificially, the time series ARIMA model of housing price level is established on the training set, relevant conclusions are drawn, and the policy of macro-control of housing prices is put forward.

1. 数据来源与描述性分析

为了研究房价的发展趋势、影响因素，以及各因素间相互作用的机制，选取上海市作为典型代表，对上海市2000年2月至2021年4月，共计243期的分月度房价、住宅销售面积、住宅开发投资额、住宅施工面积、住宅竣工面积进行分析研究。表1给出了各自变量的名称、表示字母及单位：

Table 1. The list of independent variables in the study

表1. 研究所选自变量列表

1.1. 因变量：房价

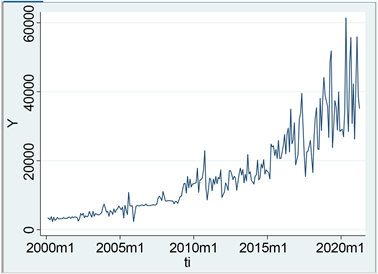
Figure 1. Timing chart of housing prices in Shanghai

图1. 上海市房价的时序图

如图1所示展示了上海市房价从2020.2至2021.4的时序图，从图1中可以看出房价整体呈现上升趋势，这与我们的现实认知是相符的。此外房价水平明显不稳定，且未表现出明显的周期性，而经过一阶差分后的序列表现出了明显的平稳趋势。

1.2. 第1个解释变量：住房销售面积

理论上来说，住宅价格应与住宅销售面积呈现负的相关关系，但是两者的二维散点图并未表现出明显的相关关系。自变量销售面积主要集中于50~300之间，且在这个值域中，几乎囊括了所有的房价范围。

1.3. 第2个解释变量：住宅开发投资额

从解释变量X₁与被解释变量Y生成的二维散点图2中可知二者具有较强的线性相关性，且是正的相关关系。我国房地产市场是一个寡头垄断市场，这一点在上海房地产市场有更明显的反映，开发商对市场的控制力比较强，而市场上的需求要远远大于市场的供给能力。事实上，近年来我国房地产开发投资额一直处于上升状态，需求的强劲推动使得它的增加并不能有效地抑制住房价格持续走高，这就使得它们与住房价格呈现正向趋势 [1]。

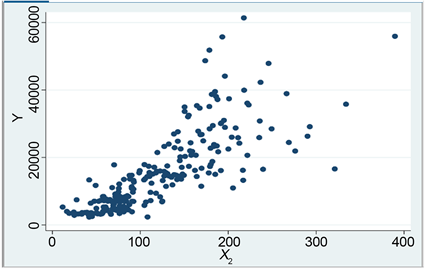
Figure 2. Y A two-dimensional scatter plot of X₂

图2. Y关于X₂的二维散点图

1.4. 第3个解释变量：住宅施工面积

目标时间段内上海市住宅施工面积主要分布在0~1000万m²，最大施工面积为6711.73万m²，最小施工面积为2.25万m²，平均施工面积约为711万m²，分布较不规律，差距较大。

1.5. 第4个解释变量：住宅竣工面积

根据图3可知，本研究范围内的住宅竣工面积属于右偏分布，且易知最大竣工面积为943万m²，最小竣工面积约为16万m²，平均竣工面积约为165万m²。

1.6. 小结

在上述分析中，首先对本报告所研究的因变量——上海市2000年2月至2021年4月的住房价格，进行了归纳与总结，房价随时间呈上升趋势，表现出明显的不稳定性和非正态性。

接着，将所选4个自变量进行描述性统计分析，并着重强调自变量与因变量之间的交互展示，结合现实因素，对它们之间的影响机制进行了初步的分析，为下一步建立数学模型提供准备。

Figure 3. Boxplot of X₄

图3. X₄的箱线图

2. 统计建模

2.1. 多元线性回归模型

2.1.1. 模型建立

根据因变量——住房价格的类型以及研究目的，本报告选择用上文所提取到的4个解释性变量进行回归分析。

首先，建立多元线性回归模型

$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+\epsilon$ (2.1)

$\hat{Y}=b_0+b_1{X}_1+b_2{X}_2+b_3{X}_3+b_4{X}_4$ (2.2)

对四个变量进行共线性检验，得到各自的方差膨胀因子如表2所示：

Table 2. Variance inflation factors for variables

表2. 变量的方差膨胀因子

以10作为判断界限，因为VIF < 10，故不存在多重共线性的问题。

将所采集到的因变量和各自变量数据带入到模型中，利用Stata软件进行多元线性回归，分析各因素对住房价格的影响程度，可以得到如表3所示的结果：

从方程整体来看，F统计量满足要求，回归方程显著；但是从T统计量的结果来看，住宅销售面积X₁对于住房价格的影响并不显著，故从方程中剔除，需要进行第二次回归。

再次将数据代入模型，进行第二次回归，得到如表4所示结果：

Table 3. Results of multiple linear regression model for housing prices

表3. 住房价格多元线性回归模型结果

Table 4. Results of the second housing price multiple linear regression model

表4. 第二次住房价格多元线性回归模型结果

从方程整体来看，F统计量满足要求，回归方程显著；而且此时每个自变量的T统计量也符合要求，即此时每个自变量对因变量的影响都是显著的。

至此，可以确定住房价格的多元线性回归方程为：

$Y=175.9+158.132X_2-2.096X_3-14.538X_4$ (2.3)

此外，根据线性回归所估计的房价与实际样本中的房价二维散点图以及回归线如图4所示：

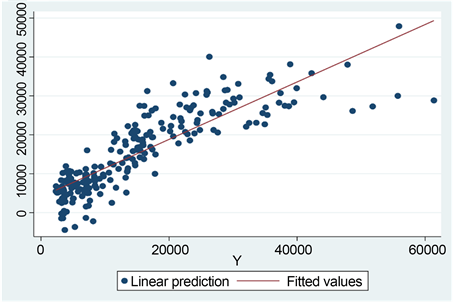
Figure 4. Scatter plot and regression straight line of actual and estimated house prices

图4. 房价实际值与估计值的散点图及回归直线

2.1.2. 模型评价

多元线性模型的残差分析主要包括正态性检验和异方差性检验。

其中正态性检验可通过做残差的直方图进行初步判断，如图5所示。

图中可以看出残差基本符合正态分布，满足正态性假设。

对于异方差性检验，本报告选择通过Stata软件进行White检验，检验结果显示Prob > chi2 = 0.0024，说明拒绝原假设，即存在异方差。接下来运用“加权最小二乘法(WLS)”对异方差进行解决和处理 [2]，求出辅助回归残差平方的倒数，即WLS权重，对模型进行调整，最后，再通过“OLS + 异方差稳健标准误”进一步确保方差依概率收敛。最终结果表5所示：

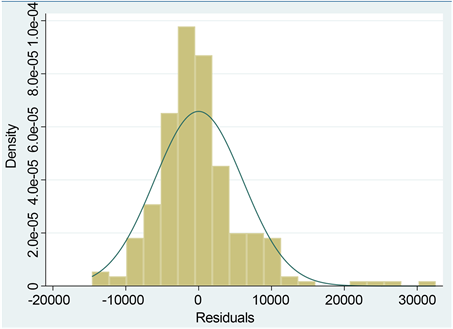
Figure 5. Regression equation residual normality test

图5. 回归方程残差正态性检验

Table 5. Regression model results after heteroscedasticity treatment

表5. 异方差处理后的回归模型结果

结果WLS处理过后的残差图如图6所示，可以看到异方差问题得到了很好的解决：

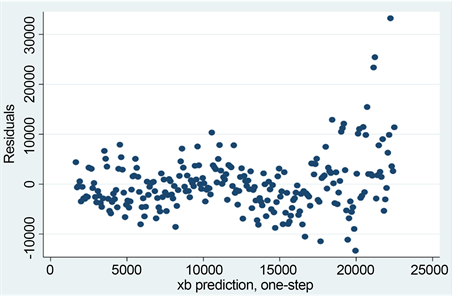
Figure 6. Residual plot after WLS treatment

图6. 经过WLS处理后的残差图

2.2. 时间序列模型

在对样本数据有了基本了解之后，下面采用时间序列方法中的ARIMA模型对房价数据进行分析。具体而言，首先将两个序列拆分为训练集(2000.1~2020.8)与测试集(2020.9~2021.4)。然后在训练集上构建ARIMA模型。

2.2.1. 检验

首先对上海市住房价格进行平稳性检验。从图1的房价时序图中可以初步判断选定时间内的上海房价序列非平稳。接下来采用Q检验对序列进行白噪声检验。检验结果显示，p值小于0.01，序列非白噪声。因此接下来尝试采用ARIMA模型提取序列信息。

2.2.2. 模型建立

对序列完成检验之后，首先画出序列的ACF和PACF图，方便辅助序列的定阶分析；然后，再通过Stata完成定阶，选择出最优的ARIMA模型。

图7给出了原始序列以及一阶差分后的ACF和PACF图，以便分析模型定阶情况。从原始序列的相关系数图中可以看出，序列的ACF和PACF均拖尾 [3]，ACF没有快速将至0附近，从而验证了序列的非平稳性。从一阶差分后的相关系数图中可以看出，在对序列进行一阶差分后，ACF和PACF的拖尾现象都有所改善，尤其是一阶差分后的ACF截尾现象较为明显，因此可以认为差分后的序列表现出了平稳趋势。

Figure 7. Original sequence and first-order differential sequence ACF and PACF plots

图7. 原始序列及一阶差分序列ACF和PACF图

现对其一阶差分序列进行DF-GLS单位根检验，检验结果表明在显著性水平0.05下显著拒绝存在单位根的原假设，说明一阶差分序列是平稳的，因此d = 1 [4]。

根据上面的自相关和偏自相关图，大致确定几个待选模型，表6展示了各个模型的显著性及其AIC值，以便取得一个较优的模型。

Table 6. Significance of the model and AIC values

表6. 模型的显著性及AIC值

根据AIC准则，AIC值越小，拟合度越高，故最终选定的模型为ARIMA (0,1,3)，拟合结果见表7：

Table 7. ARIMA (0,1,3) model results

表7. ARIMA (0,1,3)模型结果

具体公式可写为：

$\nabla x_t=-0.628{\epsilon }_{t-1}-0.36{\epsilon }_{t-2}+0.144{\epsilon }_{t-3}$ (2.4)

2.2.3. 事后检验

在对房价序列完成ARIMA模型建立后，还需要检验模型是否已提取序列的全部信息，即残差的白噪声检验，以及序列是否存在异方差问题，即进行异方差检验。

首先仍然采用Q检验对序列残差进行白噪声检验。检验结果显示p = 0.8387，残差序列为白噪声，即模型以及提取了序列中的全部信息。

接着对序列进行自相关性检验。通过Stata画出残差的自相关-偏自相关图，可以得出结论：残差不再存在自相关，说明模型拟合得很好。

最后进行异方差检验，检验结果为Prob > chi2(40) = 0.0000，即存在异方差问题。接下来尝试对模型建立GARCH模型：

2.2.4. GARCH模型

首先检验ARCH效应是否存在。通过对房价水平一阶差分进行常数回归，接着用LM检验来判断ARCH (1)效应。检验结果显示Prob > chi2 = 0.0000，说明原模型的残差序列存在ARCH (1)效应，因此，通过ARCH (1)模型来估计GARCH (1,1)的系数。最终拟合出GARCH (1,1)模型如下：

$y_t=69.945+{\epsilon }_t$ (2.5)

${\sigma }_t^2=81781.62+0.666{\epsilon }_{t-1}^2+0.593{\sigma }_{t-1}^2$ (2.6)

其中 $y_t=Y_t-Y_{t-1}$

接下来对GARCH (1,1)模型进行评估，包括序列相关性检验、残差正态分布检验以及残差白噪声检验：

画出残差以及残差平方的自相关–偏自相关图，发现不再存在序列相关性，检验通过；

通过残差的直方图可知，满足残差正态性的假设；

最后进行残差的白噪声检验，结果显示p = 0.8267，即GARCH (1,1)模型的残差为白噪声。

综上所诉，GARCH (1,1)模型的建立较好的解决了原模型的异方差问题，且拟合效果较好。

3. 结论和建议

3.1. 结论

本报告首先通过收集2000年2月至2021年4月上海房地产市场有关数据，通过建立多元线性回归方程，对上海房价的影响因素进行深入研究，得出结论：对上海住房价格影响显著的几个因素包括住宅开发投资额、住宅施工面积以及住宅竣工面积，其中房价与住宅开发投资额成正相关关系，与住宅施工面积、住宅竣工面积成负相关关系。

接着对房价水平进行时间序列分析，具体而言，将样本划分为训练集和测试集，然后采用时间序列中的ARIMA模型对房价序列进行建模分析，并最终建立了拟合效果较好的GARCH (1,1)模型。

3.2. 我国房地产宏观调控政策建议

首先应当认识到我国是社会主义市场经济体制，这是国家和政府采取任何政策措施的大前提。在市场经济中，商品的价格主要由市场交易决定，政府一般不能动用行政手段对其进行干涉 [1]。在制定我国房地产宏观调控政策时，同样应该遵循这个规则，不到迫不得已的情形，不主动干预房价，防止扰乱市场秩序。

其次，我国政府和有关部门制定房地产宏观调控政策措施的目的，不是让所有人都能全款买房，也不是放任越来越多的人“炒房”，而是要使“居者有其屋”，解决大部分国人温饱问题的下一步，就是解决普通老百姓“住”的难题。主要措施有：

1) 坚持小户型为主的开发政策。我国虽地大物博，但人口数量众多，地区发展不平衡，东部地区土地资源十分有限，在土地供给总量一时无法得到改善的情况下，主张小面积住宅能够有效缓解住房压力，避免铺张浪费。

2) 完善住房保障体系，健全经济适用住房体系；

3) 科学合理地进行城市规划工作。首先，要加强对城市发展的评估与预测，及早做好城市规划、居住用地布局规划；其次，要平衡大都市区发展，形成多中心的城市空间结构 [1]。