1. 引言
空气滤清器受到发动机的激励以及高速气流的影响,导致辐射噪声的产生,噪声的产生容易导致空气滤清器发生共振作用导致疲劳破坏,使其报废 [1] [2]。关英俊等人 [3] 在有限元仿真软件中建立了空气滤清器的有限元模型,并对其进行了模态分析和结构优化。刘士军等人 [4] 针对当前汽车部件中的空气滤清器结构,构建有限元模型并分析,从而获得汽车空气滤清器的刚度数值,并进行了相应分析。张宇等人 [5] 以某空气滤清器为研究对象,基于有限元方法并结合空气滤清器的实际工况进行振动疲劳分析,并进行了试验验证。栾宝奇等人 [6] 通过机车空气滤清器整机试验台的研发,改进试验方法和试验装置,并阐述了不同试验方法对试验结果的影响。
综合上述分析,对空气滤清器的振动特性和优化方法有仿真分析法和试验法。本文基于有限元仿真软件Abaqus对某车型空气滤清器进行振动特性分析,得到空气滤清器模态分析结果。考虑到空气滤清器的工作状况,以提高其固有频率为目的,对现有的结构进行优化设计,避免与外部激振作用发生共振,提高空气滤清器的工作性能和系统的稳定性。
2. 空气滤清器几何模型建立
本文以某汽车的空气滤清器作为分析对象,首先,根据空气滤清器的实物模型在SolidWorks中创建三维模型,之后导入Abaqus仿真软件,通过网格划分、添加约束及边界条件后进行振动特性分析。图1所示为本文空气滤清器的三维模型,模型主要包括壳体,滤芯,垫圈,端盖几个部分。其材料为PP + TD40塑料材质,弹性模量为2450 MPa,密度为1220 kg/m3,泊松比为0.41 [3]。
3. 空气滤清器模态分析
3.1. 模态分析概述
模态分析作为一种重要的故障检测和结构分析方法,应用在各大领域,是工程实践设计过程中的重要一环 [7]。模态分析可分为自由和约束模态分析两种,实质上,模态是系统的固有属性,只由其材料自身属性和结构决定,与外部激励等其他因素并无关系。
对任意一个系统,其结构的振动微分方程为:
(1)
式中,
为系统质量矩阵,
为系统阻尼矩阵,
为系统刚度矩阵;
为外部激励载荷矩阵;
为系统各点的广义向量。
空气滤清器在忽略阻尼的情况下,系统的自由振动微分方程可表示为:
(2)
根据公式求解可得该空气滤清器的各阶固有频率及振型。
3.2. 模态分析
3.2.1. 模型的建立和网格的划分
同一系统的动态特性会随着约束方式的变化而变化,因此,为了保证仿真的真实性及准确性,在对系统进行模态分析前需要分析系统的约束。考虑到本文滤清器的安装方式,可以得到该滤清器有三处约束,分别是两个出气口与汽车其他部件的连接约束、壳体底座与汽车的连接约束,如图2所示。
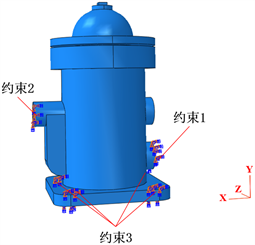
Figure 2. Three restraint positions of air filter structure
图2. 空气滤清器结构的三处约束位置
在Abaqus中利用网格划分模块对滤清器结构的整个计算域进行网格划分。网格划分的精度和质量会对模态分析结果产生较大影响,网格的不规则会导致仿真结果误差较大,同时本文考虑到仿真计算时圆角结构对模态分析的影响,将网格划分四面体网格,网格单元类型为C3D10,网格单元数和节点数分别为201,304及314,105,如图3所示。
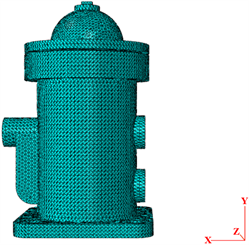
Figure 3. Air filter structure meshing
图3. 空气滤清器结构网格划分
3.2.2. 模态分析结果
根据机械振动理论可知,任意系统都具有无限阶的固有频率,但工程实践中影响系统稳定性的只有前几阶固有频率 [8]。所以,本文在有限元软件中只分析空气滤清器的前6阶固有频率和振型。下图4为空气滤清器的前6阶振型图,由图4可知每一阶的共振部分和振型变形量的大小是不同的;由于两出气口和壳体底座有约束,因此其周边没有出现较大的振幅,这于空气滤清器的正常工况相符合。
由上图4可得空气滤清器的前6阶固有频率值,如下表1所示。由表1可知,空气滤清器在约束条件下从1阶至6阶固有频率大小为246.52~786.89 Hz。

Table 1. The first 6-order natural frequency and mode characteristics of air filter
表1. 空气滤清器前6阶固有频率和振型特征
将上表1中固有频率数值随阶数变化的柱状图绘制于下图5中。
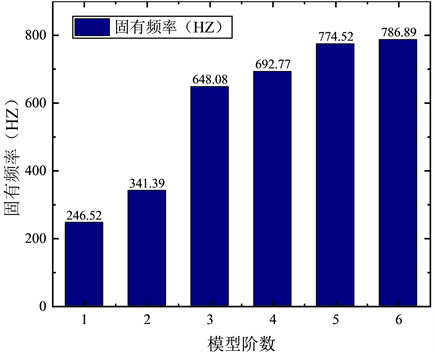
Figure 5. Bar graph of natural frequency with order
图5. 固有频率随阶数变化的柱状图
从上图5可知,空气滤清器在约束条件下从1阶至6阶固有频率逐渐增大,第2阶至第3阶固有频率增幅最大,第5阶至第6阶固有频率增幅最小,这与空气滤清器的结构及其材料属性是有很大关系的。
4. 空气滤清器优化设计
4.1. 优化设计方案的提出
在保证空气滤清器进出口流量等性能参数不变的前期下,对现有的空气滤清器进行结构优化。优化方案A:PP + GF30塑料材质是空气滤清器常用的一种材料,其密度为1130 kg/m3,弹性模量为5800 MPa,泊松比为0.4 [2],此方案将原有的材料替换为PP + GF30塑料材质;优化方案B:考虑到空气滤清器是薄壁类零件,此优化方案中将空气滤清器壳体外壁及壳体底座进行各加厚2 mm处理,如下图6(a)所示;优化方案C:考虑到壳体底座是约束在汽车上的,此优化方案在壳体底座周边增设四个厚度为8 mm的三角形加强筋,如下图6(b)所示。
 (a)
(a)  (b)
(b)
Figure 6. 3D models of optimization plan B and optimization plan C. (a) 3D model of optimization plan B; (b) 3D model of optimization plan C
图6. 优化方案B及优化方案C的三维模型。(a) 优化方案B的三维模型;(b) 优化方案C的三维模型
4.2. 优化方案结果分析
基于动态特性分析方法,对三种优化方案进行分析,三种优化方案的仿真结果如下图7、图8、图9所示。
根据上图7、图8、图9的优化方案仿真结果,得到三种优化方案的前6阶固有频率,并计算了各个方案固有频率相对原方案的增加比率,如下表2所示。

Table 2. Natural frequency and increase ratio of three optimization schemes
表2. 三种优化方案固有频率值和增加比率
根据上表2中三种优化方案的6阶固有频率数值,结合表1中空气滤清器优化前的6阶固有频率数值,对比空气滤清器优化前后固有频率变化趋势,如下图10所示。

Figure 10. Six order natural frequency variation trend before and after air filter optimization
图10. 空气滤清器优化前后6阶固有频率变化趋势
由上表2及图10可知,不管优化与否,空气滤清器的6阶固有频率均呈现增大趋势,且第2阶至第3阶固有频率增速最快。相比于原方案,优化方案A从1阶至6阶固有频率均大幅度增加,平均增加比率为59.60%,优化方案A中PP + GF30塑料材质由于其刚性较大,因此不容易变形,故而其固有频率较高;与原方案相比,优化方案B从1至5阶固有频率均有所增加,第6阶固有频率有微小的减少,平均增加比率为3.82%;与原方案相比,优化方案C的6阶固有频率基本没有变化,平均增加比率为0.07%。综上,从空气滤清器使用寿命及其经济性角度出发,考率到PP + GF30塑料材质的成本较高,故优化方案B即将空气滤清器壳体外壁及壳体底座进行各加厚2 mm,满足结构优化要求。
5. 结论
本文以某汽车空气滤清器为研究对象,基于三维软件SolidWorks建立空气滤清器几何模型,并在有限元仿真软件Abaqus中对其进行了约束模态分析,仿真结果表明该空气滤清器的基频(1阶固有频率)为246.52 Hz,固有频率从1阶至6阶依次增大,第6阶固有频率为786.89 Hz。本文针对该空气滤清器提出的三种优化方案中,考虑到空气滤清器使用寿命及其经济性问题,优化方案B即将空气滤清器壳体外壁及壳体底座进行各加厚2 mm,能使空气滤清器的各阶固有频率都有所提高,基频提高6.33%,1阶至6阶固有频率总体提高3.82%,优化后的结构达到了较为满意的效果。