1. 引言
在金融市场的业务场景中每天都涉及大量的资金流入和流出,面对庞大的用户群,资金管理压力会非常大。在既保证资金流动性风险最小,又满足日常业务运转的情况下,精准地预测资金流入流出情况变得尤为重要。
支付宝所推出的余额宝作为一个货币的理财工具,可以随借随取,使得用户能够更加方便地管理自己的资金。每天大量的资金流入和流出对于资金管理的压力很大,因此需要进行一个预测,来判断未来一段时间资金流入流出的情况。如果预测准确,对于用户的资金管理来说是非常有利的,而如果预测结果偏差,资金流的突然增加和减少都有可能造成一定的系统性风险,而造成严重的损失。但是金融数据往往受经济、政治等多方因素的影响,数据不稳定,这给资金流量的预测带来了难度。
本文通过采用不同时间序列算法对余额宝用户的申购赎回数据的把握,比较不同模型对于未来每日的资金流入流出情况的预测精准性,从而分析不同算法模型在对应场景中的适应性与泛化性。对于货币基金而言,资金流入意味着用户申购行为,资金流出意味着用户赎回行为。
2. 文献综述
金融时间序列预测研究是根据过去若干个历史数据的波动,建立模型来描述金融结构并预测时间序列上未来某一点的值。根据实际场景可以应用在不同的金融领域中,比如对于股票、财政、税收等领域的资金预测,这对于投资者和金融机构来说具有重要的研究意义,除此之外也可以对电商流量或者各类理财产品利率进行预测 [1]。
股票市场在金融领域占据重要的地位,因此对股票和指数的预测一直以来都是海内外学者研究和探索的课题。但股票市场的价格走势收到经济、政治、军事等诸多因素的影响,因此想要单纯的依靠理论分析就对于市场有精准的把控变得较为困难,往往预测效果不佳。因此过多的研究倾向于使用统计学或者人工智能的技术,例如郝继升等基于自适应遗传算法优化的BP神经网络对股票价格进行了预测,结果表明该模型在股票预测的精度方面得到了明显的提升 [2]。Devi,B等人的方法是使用ARIMA模型对股票趋势的有效时间序列进行分析预测,使用了不同参数的ARIMA模型对于公司过去5年的股票数据进行了建模,通过训练之后的时间序列模型来预测未来公司股价的波动趋势 [3]。Adebiyi A A的团队同样运用了ARIMA模型建立了股票预测模型,通过对纽交所和尼日利亚证券交易所的股票数据进行收集和训练,结果表明,自回归移动平均模型在股票短期预测上有着一定的优势 [4]。但同时ARIMA模型在使用上也有着一定的局限性,ARIMA模型要求输入的时间序列是稳定的序列,但在实际情况中大部分的金融数据并不一定是平稳的,因此对于一些股价波动剧烈的股票类型来说,ARMA/ARIMA模型并不具有泛用性和普适性。
金融时序的预测研究对各行业的资金流量预测应用也较为广泛。国内的研究如葛娜等基于ARIMA模型对某品牌鞋类的销售量进行预测,分析结果表明该模型可以达到较好的效果 [5]。陶佳等基于改进支持向量机的方法对于林业资金投资进行了预测,与传统方法相比预测精度的提升显著 [6]。赖慧慧使用Prophet模型对乘用车的消费税进行了预测,这在行业分品目的税收预测上是一个全新的思路,结果证明Prophet在预测具有季节性和节假日特征的税收预测的方面精度高,具有优势 [7]。黄莺等使用多维灰色模型GM (1, N)模型和Prophet模型结合的方式对于电商行业的销售量进行了预测,分析出这样的组合模型适用性更高 [8]。国外研究例如Safari等将指数平滑模型和神经网络进行融合对石油价格进行预测研究,结果表明相对于传统时间序列方法有较高的准确率 [9]。
3. 模型概述
3.1. ARMA/ARIMA模型
ARMA/ARIMA时间序列模型是一组依赖于时间的随机变量。
1) ARMA模型:(Auto Regressive Moving Average自回归滑动平均模型)
ARMA模型,即AR (Auto Regressive自回归模型)和(MA Moving Average滑动平均模型)模型的结合。相比于AR和MA模型,它的准确度更高,其存在p,q两个阶数,称为ARMA (p, q)模型,表达式为:
其中,
为自回归系数,
表示白噪声,是时间序列数值的随机波动。
ARMA模型结合了AR和MA模型的特点,AR解决了前后数据之间的关系,MA则解决了随机变动即噪声的问题,因此其可以拟合所有的时间序列。但是,该模型是基于平稳数据建立的。
2) ARIMA模型:(Auto Regressive,Integrated Moving Average差分自回归滑动平均模型)
由于实际中很多数据都是不平稳的数据,差分的过程就是把输入的不平稳数据平稳化,即将前后两个数据进行减法操作。相较于ARMA,ARIMA增添了一个差分的操作,将不平稳的数据进行差分平稳。ARIMA具有三个阶数,p,d,q,称为ARIMA (p, d, q)模型,d表示差分阶数。因此在对ARIMA模型进行拟合之前,需要判断数据是否为平稳序列 [10]。对于非平稳的数据需要先进行d阶差分运算,化为平稳的时间序列。在使用ARIMA模型进行预测后还需要对预测数据进行还原的操作,图1为该时间序列模型具体流程图。
3.2. Prophet模型
Prophet作为Facebook的一个开源的时间序列预测模型,相比ARMA/ARIMA模型可以设置饱和增长,突变点,节日与大事件等参数。在Prophet的模型预测中,它不会给出一个确切的数字,而会给出一个上下波动的范围,这样的预测区间会更加合理,并且不容易发生过拟合。
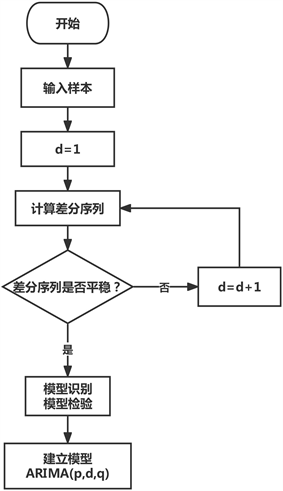
Figure 1. Specific flow chart of time series model
图1. 时间序列模型具体流程图
Prophet是一个基于加法模型(Additive Model)的时间预测,其加法原理就是把一个原始数据拆成几个部分做累加的过程,可以比较精准的去预测非线性的周期趋势。同时Prophet的优势在于添加了Holiday影响因子,可以很好的对例如十一假期、春节等节假日带来的活跃数据的突变进行预测,如中国传统节日春节,在这个期间人们会购买大量新商品,造成资金流发生明显的变化,因此这些大事件前后的日期将会被单独考虑,并且通过拟合附加的参数模拟节假日和事件的效果。
Prophet的数学模型可以表示为:
其中,g(t)代表趋势项,用来表示时间序列中非周期性的变化;s(t)代表周期项,用来表示时间序列中周期性的变化。
3.3. 周期因子时间序列模型
很多时间序列都具有明显的周期性,例如购物、客流量等,对于通勤人数来说,周一的流量最大而周末的流量最小,类似于此类数据都会呈现出一个周期性的波动趋势,因此需要考虑周期因素,在预测之前需要确定周期长度,比如一周或者一个月。
对于周期波动非常明显的数据,使用ARMA/ARIMA模型进行预测的准确度就会下降,ARIMA的原理是用过去的几个时间点预测下一个时间点,含有趋势性,但运用在含周期因素的数据中,预测结果就会出现较大的偏差。
因此使用周期因子预测时间序列的核心任务是尽可能准确的提取出周期特征weekday,具体操作为获取周一到周日的均值,再除以整体均值即可得到因子数。第二步需要设定一个基数base,可以选取最后一周的均值作为基数,最后使用base值乘上周期因子进行预测,具体流程如图2所示:

Figure 2. Flow chart of periodic factor prediction
图2. 周期因子预测流程图
对于不含趋势性相对稳定且周期性强的时间序列而言,采取周期因子的时间序列预测会更合理。
4. 互联网金融资金流数据分析
本次研究数据来源于由阿里云提供的“资金流输入输出预测”大赛数据。数据集一共包含四个部分:用户基本信息数据、用户申购赎回数据、收益率表和银行间拆借利率表。本文主要使用的是用户申购赎回数据表,记录了2.8万用户在427天内的操作情况,其中操作记录包括申购和赎回两个部分,金额的单位为分,即0.01元。数据经过了脱敏确保了安全性,同时保证了:今日余额 = 昨日余额 + 今日申购 − 今日赎回,不会出现负值。
本文使用的数据集包含了余额宝资金流的详细信息。由于单个余额宝的交易记录是以用户维度来进行记录的,但是单用户的余额宝使用行为缺乏规律性,且各个用户的理财习惯和消费风格均有差异,因此对于单个用户的资金流预测较为困难。基于此,本文按照日期这一维度进行了预测和分析,即对所有用户的交易记录进行了聚合和加总的操作,预测分析的是所有用户每一天的总购买量与总赎回量 [11]。对数据集进行聚合操作,按照日期进行聚合,将同一时间进行加和处理,统计每一天的总的购买量与申购量,得到一个2*247维的数据集。
分别提取申购量与赎回量的总体数据并将统计好后的数据可视化如图3所示:
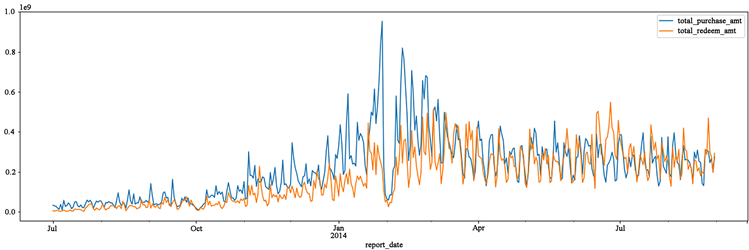
Figure 3. Time series of total daily purchases and redeems
图3. 每日总购买与赎回量的时间序列图
在分析过程中,为了明确模型的拟合效果,并与真实数据进行对比计算误差,需要将数据集分为训练集(train-data)和测试集(test-data),本文选取前13个月即2013年7月1日到2014年7月30日的数据为训练集,选取最后一个月即2014年8月份的数据为测试集进行模型的拟合。按照统计学的方法将时间序列进行拆解后,对于指定时间范围的数据进行可视化分析,分析结果如图4所示:
由上图可以看出,趋势性在一开始一直向上,达到一定高峰后开始下降,一开始的趋势很明显,分析可得前期属于一个推广期,用户数量不多,而在后期随着用户数量的增加,已逐渐趋于稳定。
5. 三个模型的预测比较
在使用时间序列模型ARMA/ARIMA建模之前需要对数据进行平稳性检测,本文使用的检测方法为统计学中的ADF检测,按照小概率事件原则进行检验。
ADF检验需要进行假设检验,假设检验过程如下所示:
原假设H0:序列不平稳;备择假设H1:序列平稳。
如果统计所得的显著性检验统计量小于三个置信度1%,5%,10%,则分别对应有99%,95%,90%的把握拒绝原假设。分别对于申购量与赎回量数据集进行统计量计算可得,原始数据的统计量分别为−1.590和−1.372,大于置信度为10%的统计数值,落入接受域,因此没有充分理由拒绝原假设,即证明原始数据是非平稳的。
对数据集进行一阶差分后再进行假设检验,在进行差分后会出现空值,因此还需要删除缺失值后在进行检验,差分前后统计数值如表1所示:

Table 1. Numerical statistics before and after difference
表1. 差分前后数值统计
由上述ADF平稳性检测可得,在使用时间序列模型ARIMA进行预测时,设置参数d为1,即需要进行一阶差分,保证数据为平稳序列后在进行拟合 [12]。
模型通过上述检验后,使用训练集对模型进行拟合和预测,为了更直观的说明预测精度,将预测结果和测试集的实际结果进行对比如图5和图6所示来分析误差。
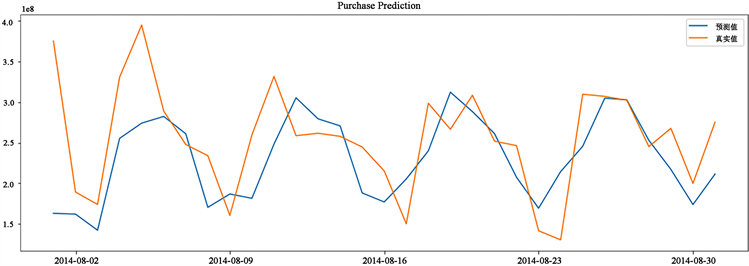
Figure 5. Prediction comparison of purchase model
图5. 申购模型预测对比
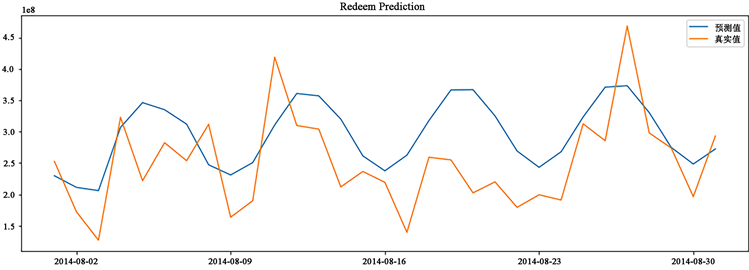
Figure 6. Comparison of redemption model predictions
图6. 赎回模型预测对比
ARIMA模型在经过差分处理后提高了精确度,因为经过差分后数据更加平稳,规律也更加清晰。由于ARMA模型是在统计学的基础上建立起来的,考虑的特征因素较为单一,在预测的过程中更为便捷与直观,同时应用场景广泛,只要与时间序列相关的数据都可以进行运用,不需要调整过多的参数就可以迅速给出一个参考数值作为判断依据。但同时其也存在着局限性:首先,ARMA需要时序数据是稳定的,而现实中的数据大多情况下都有自己的趋势,很难做到完全平稳。其次,ARIMA模型为线性模型,无法处理非线性的关系。
除此之外,经过相关资料的查询与分析,使用ARIMA模型进行金融数据的预测,例如股票预测往往会出现过拟合的情况,究其原因,是因为其预测是存在一些惯性的,但是股市是存在噪音的,例如突发事件可能造成市场的急转直下,所以预测是后知后觉所进行的一个变换,而这些变换会作为已知值传入到预测模型中,数据也会随之发生一些变换,因此从数据的显示中可以看出预测总是存在滞后性,导致许多表面看起来很完美的预测结果,可能只适合于过去,而无法应对未来所发生的的一些未知事件 [13]。
在使用Prophet模型进行预测时,将训练组数据代入Prophet模型可得到许多参数,包含了预测值的上下限,趋势的上下限等数值,具体的预测结果如图7与图8所示,展示了预测的上下波动范围,同时显示了突变点,这其中涵盖了许多市场突发的变化所带来的噪音,随着突变点数量的增多,模型拟合就变得更加了灵活。
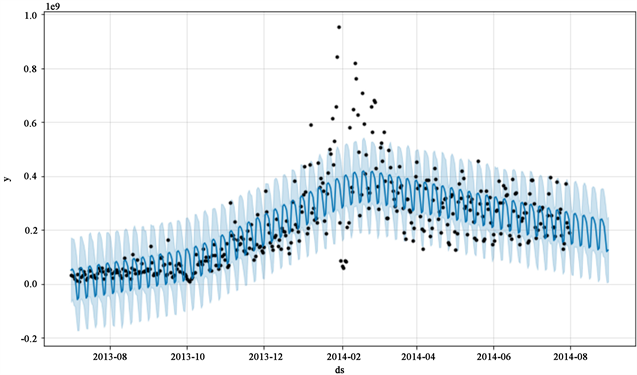
Figure 7. Forecast results of purchase model prophet
图7. 申购模型prophet预测结果
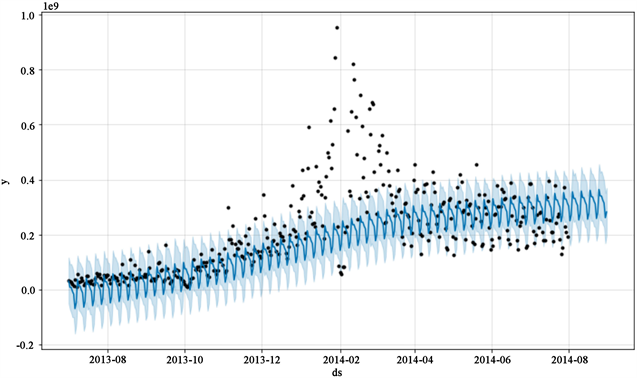
Figure 8. Prediction results of redemption model prophet
图8. 赎回模型prophet预测结果
通过Prophet预测结果与ARIMA模型对比如图9可以看出Prophet与ARIMA的模型的拟合效果相差不大,通过特征提取申购量的周期属性(weekday)可以发现用户在一周之内的不同时间点的行为具有一定的规律,如图10所示,按照weekday特征经过统计得出如下图所示的规律,可以看出周一,周二的用户申购量最多,而周五和周六的数量最低。根据余额宝的收益显示规则进行分析,周五周六所产生的收益用户在下周才能知晓,因此如果没有特殊情况,大部分用户会选择在周一或周二进行申购行为而不会选择在周末。
通过分析,显然weekday是一个非常明显的特征,因此需要在模型拟合的过程中考虑在内。
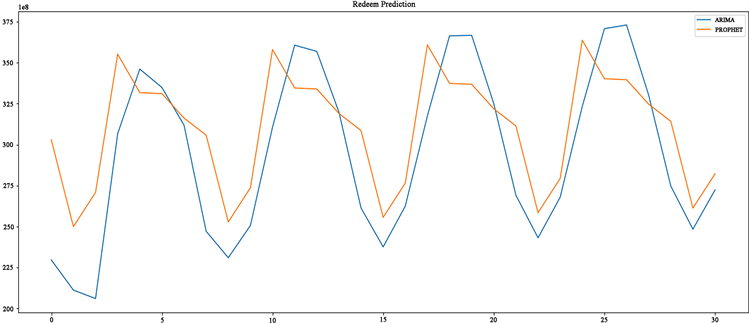
Figure 9. Prediction results of redemption volume by prophet and ARIMA models
图9. Prophet与ARIMA模型对赎回量预测结果
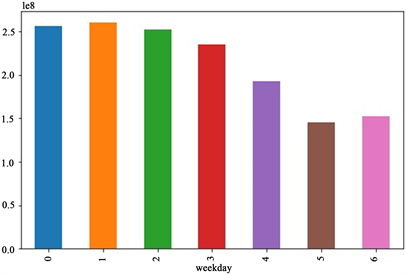
Figure 10. Subscription quantity of users at different times of the week (0 for Monday, 6 for Sunday)
图10. 用户在一周不同时间的申购数量(0代表周一,6代表周日)
基于上述分析,由于数据集存在一个非常明显的用户周期性行为,因此使用了周期因子时间序列模型进行预测。针对资金流入流出的预测,需要预测的是8月份每天的流量,base可以取1~30号的平均流量,乘上周期因子后得出结果。根据上述计算步骤,首先需要计算周期因子weekday,再计算出1号至30号的均值。需要注意的是,在计算每日均值时会受到周期因子weekday的影响,因此需要统计weekday在每日出现的频率,剔除周期因子对于每日均值的影响后再将该数值作为base,最终根据每日的base和周期因子进行预测。
由于使用周期因子的方法进行预测需要保证数据集是稳定的,根据时间序列分解可以看出,在2014年4月之后数据集趋于稳定,因此截取14年4月至7月的数据进行周期因子计算,并由此进行相关预测。如图11所示,根据这一段时期内周一至周日的购买与赎回总量与总均值的比值得出周一至周日的周期因子,其中的purchase_weekday与redeem_weekday分别代表用户申购量与赎回量的周期因子,可以明显比较出周一的数值最大,而周六与周日的数值相对较小。
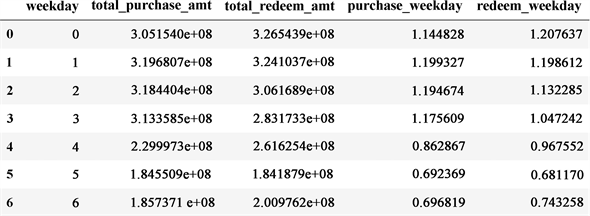
Figure 11. Calculation results of cycle factor from Monday to Sunday
图11. 周一至周日的周期因子计算结果
分别统计周一到周日在1号与31号的频次计算出周期因子对于每一天的影响力day_rate,在按照日期计算每一天的均值day_mean,根据两者的比值即可得到所需的base,最后将周期因子乘上base可得出最终预测结果。
基于周期因子的时间序列预测模型虽然无法考虑到节假日和突发事件等情况,但基于本文数据集在后没有明显向上或向下的趋势且周期性较强,因此通过计算后发现使用该模型拟合效果良好。将所预测结果与前两种模型进行对比如图12所示。
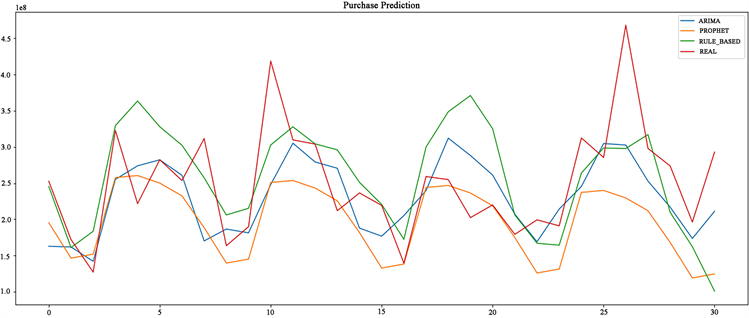 (a)
(a)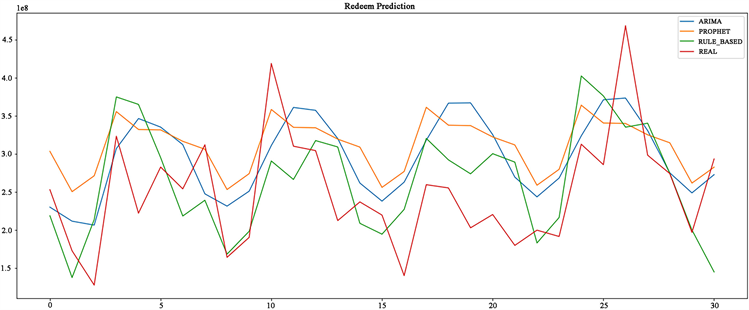 (b)
(b)
Figure 12. Comparison of model prediction results
图12. 模型预测结果对比
通过计算
与均方根误差RMSE来检验模型的拟合效果,如果
越接近于1且RMSE越小,则说明模型的预测效果越好。如表2与表3所示,可以看出不论是申购量还是赎回量的预测,基于周期因子的时间序列模型在进行了数据裁剪,数据集较小的情况下,RMSE仍然相对较小,说明其预测效果是不错的。

Table 2. Comparison of purchase prediction accuracy of three models
表2. 三种模型申购量预测精度对比

Table 3. Comparison of redeem prediction accuracy of three models
表3. 三种模型赎回量预测精度对比
6. 结论
本文针对余额宝的资金流入流出问题进行了模型拟合与数值分析,分别使用了ARMA/ARIMA时间序列模型、Prophet模型和基于周期因子的时间序列方法对其进行了统计和拟合,图13和图14是对三种模型与真实值的比较,预测值1是ARIMA模型的预测结果,预测值2是Prophet模型的预测结果,预测值3是周期因子的预测结果。
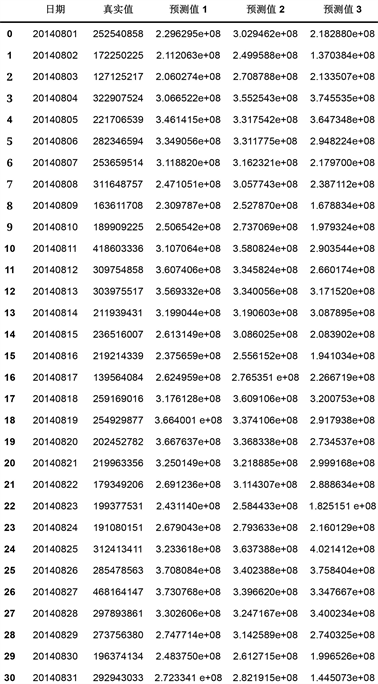
Figure 13. Prediction results of three prediction models for purchase volume
图13. 三种预测模型对于申购量的预测结果
基于上述预测结果主要得出了以下结论:
1) ARIMA模型、Prophet模型和基于周期因子的时间序列预测方法对于资金流量数据均有较好的拟合效果,三种模型的预测精度均在0.2左右。但由于其内部逻辑的不同,基于周期因子的预测方法相较于前两种模型预测的结果相对更加准确,因为其考虑了序列中非常重要的周期性特征。
2) ARIMA模型属于探索性预测模型,是基于统计学基础建立起来的模型,在预测过程中更为简便,主要依赖于时间特征进行建模,很少加入其他参数的影响例如环境限制或周期性变化。因此在进行时间序列预测的前期可以使用该模型迅速得出参考性标准,但若是要追求模型的精确度,可能在后期需要添加更多的影响因素以提高模型的泛化性,防止出现过拟合的情况。
3) Prophet的优点在于在拟合过程中可以人为设置许多参数,例如容量值、突变点以及季节性和节假日,可以预测非线性的周期趋势,大大增强了模型的泛化性。对于商业领域的金融数据分析,Prophet可以进行很好的预测,但可能不适用于一些周期性或趋势性不显著的时间序列。
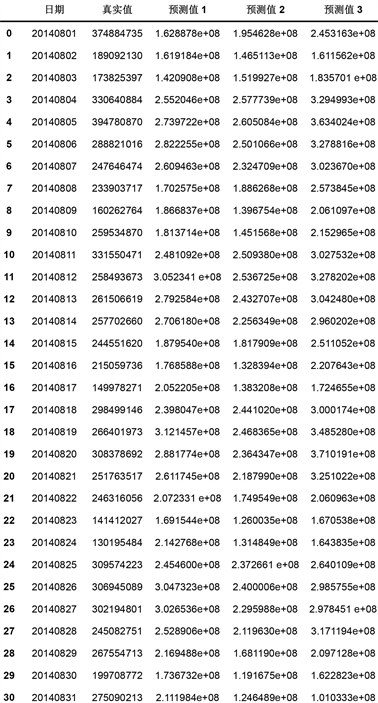
Figure14. The prediction results of three prediction models for redemption volume
图14. 三种预测模型对于赎回量的预测结果
基于周期因子的时间序列分析在本文的拟合效果最优,因其加入了一个非常重要的影响因素,即用户在一周之内不同时间的操作行为具有非常明显的周期性。对于较为平稳的周期性时间序列,基于周期因子的时间序列方法可以达到比较好的预测结果,但该方法只适用于一些特定的时间序列,且只适用于短期预测。