基于多体系统理论的机床几何误差预测模型

Machine Tool Geometric Error Prediction Model Based on Multi-Body System Theory

摘要: 针对五轴机床几何误差建模，首先，从分析误差产生机制和建立精度误差补偿模型的角度，提出了基于多体系统理论的平动轴几何误差模型；其次，依据误差模型，对运动轴联动所产生的圆弧轨迹进行了预测，并与球杆仪实测圆轨迹进行对比验证；同时，依据三角函数法对球杆仪偏置误差进行了分离和辨识，还原出实际的几何误差；最后，实验表明所提方法能有效地去除球杆仪检测时引入的偏置误差，经误差模型预测的圆度与球杆仪实测值的误差百分比为4.2%，所提预测方法效果显著。

Abstract: Aiming at the geometric error modeling of five-axis machine tools, firstly, a translational axis geometric error model based on multi-body system theory was proposed from the angle of analyzing error generation mechanism and establishing accuracy error compensation model. Secondly, according to the error model, the arc trajectory generated by the motion axis linkage was predicted, and compared with the measured circle trajectory of the cue instrument. At the same time, according to trigonometric function method, the bias errors of the cue apparatus are separated and identified, and the actual geometric errors are restored. Finally, the experimental results show that the proposed method can effectively remove the bias errors introduced by the rod tester, and the error percentage between the roundness predicted by the error model and the measured value of the rod tester is 4.2%, indicating that the proposed method is effective.

1. 引言

机床几何误差检测和建模是实现误差补偿的前提条件，五轴机床综合误差模型表示了刀具切削点与被切削点之间的偏差，该偏差是由平动轴和旋转轴引起的综合误差，针对平动轴，建立合理的平动轴误差模型是辨识空间误差的必要保证 [1]。多体系统理论建模法是目前较为成熟的理论，刘又午基于多体系统理论建立了包含几何误差和热误差的机床综合误差模型 [2]，付国强基于多体系统理论建立了五轴机床刀具相对于工作台的综合误差模型 [3]，王涛基于多体系统理论建立了五轴机床旋转轴的误差模型，并推导出误差测量值与各项误差参数的关系模型 [4]。

在几何误差检测及模型验证方面，常用仪器有激光干涉仪 [5]、探针 [6]、球杆仪 [7] 等，其中，球杆仪价格低廉、操作简单，经过简单的圆轨迹测试就可以快速测量出运动过程中球杆仪长度变化量。机床两轴或者多轴联动时得到圆弧轨迹，利用圆轨迹可以对机床综合误差快速评定。李巍采用圆轨迹对五轴机床直线轴及旋转轴误差插补模型进行了验证 [8]，梁莹莹以五轴机床作为载体，使用球杆仪圆轨迹进行几何误差分析 [9]。球杆仪安装时，由于底座轴线与目标轴线不完全重合，产生了偏置误差，有效地对采集的数据进行去偏心处理、对真实的误差数据进行还原是利用球杆仪检测数据进行分析的前提，也是实现对任意圆轨迹误差预测的必要条件。Zargarbashi等提出了一种球杆仪模型，可以消除球杆仪偏置误差的影响 [10]，邵圳将旋转轴上被测点的运动轨迹进行拟合，确定了旋转轴在三维空间中的实际位置，计算出旋转轴的安装误差 [11]，然而，以上方法较为复杂、耗时长。

因此，本文依据多体系统理论对五轴机床平动轴误差进行建模，利用球杆仪对机床平动轴进行空间圆度的测量，依据圆轨迹法对误差模型进行验证。其次，提出了一种基于三角函数拟合的方法，通过分析机床运动过程中偏置误差对球杆仪杆长的影响，从测量结果中分离出偏置误差。

2. 五轴机床几何误差建模

五轴机床一般由X、Y、Z三个直线轴和两根旋转轴、主轴等部件组成，结构如图1所示。由于机床零部件的制造和偏置误差，机床移动轴沿导轨运动时，会产生六项几何误差，以X轴为例，分别为三项线性误差： ${\delta }_x\left(x\right)$ 、 ${\delta }_y\left(x\right)$ 、 ${\delta }_z\left(x\right)$，和三项转角误差： ${\epsilon }_x\left(x\right)$ 、 ${\epsilon }_y\left(x\right)$ 、 ${\epsilon }_z\left(x\right)$，如图2所示。

根据多体系统齐次坐标变化的建模方法，以床身作为参考坐标系，在各运动部件上分别建立各自的局部坐标系，将旋转轴看为静止刚体，将五轴立式机床分解为两条运动链：刀具运动链：O→X→Z→T；工作台运动链：O→Y→W。理想情况下在运动时刀尖点和切削点是重合的，然而实际情况下，由于误差的存在，机床发出命令时刀具不会到达理想位置，X、Y、Z轴运动后，运动链末端点的实际位置与理想位置的偏差量E为：

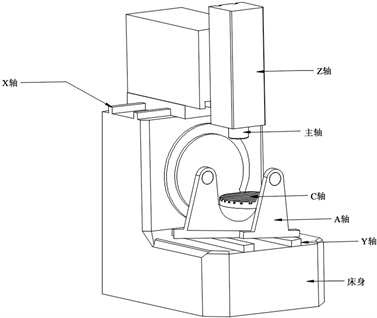
Figure 1. Structure diagram of TTTRR machine tool

图1. TTTRR型机床结构图

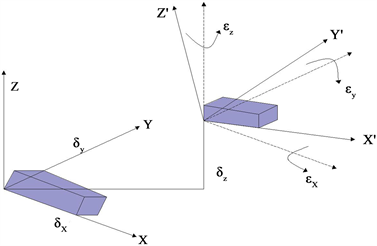
Figure 2. Geometric error diagram of X axis

图2. X轴几何误差示意图

$\begin{array}{l}E={P^{\prime }}_T-{P^{\prime }}_W\\ {P^{\prime }}_W=T_Y\cdot \Delta T_Y\cdot P_W\\ {P^{\prime }}_T=T_X\cdot \Delta T_X\cdot T_Z\cdot \Delta T_Z\cdot P_T\end{array}$ (1)

式中， ${P^{\prime }}_T$ 和 ${P^{\prime }}_W$ 分别表示刀具切削点和工件上对应点在床身坐标系下的坐标； $P_T$ 表示刀具切削点在刀具坐标系内的坐标； $P_W$ 表示工件对应点在工件坐标系内的坐标； $T_X$ 、 $T_Y$ 、 $T_Z$ 和 $\Delta T_X$ 、 $\Delta T_Y$ 、 $\Delta T_Z$ 分别表示X、Y、Z轴的理想运动矩阵和运动误差矩阵。

由式(1)可以得到刀具切削点相对于工件的空间位置误差在X、Y、Z轴方向上的分量：

$\{\begin{array}{l}\Delta x_s={\delta }_x\left(x\right)-{\delta }_x\left(y\right)+{\delta }_x\left(z\right)-y{\epsilon }_z\left(y\right)+z{\epsilon }_y\left(x\right)-z{\epsilon }_y\left(y\right)+y{S}_x\left(y\right)-z{S}_x\left(z\right)\\ \Delta y_s={\delta }_y\left(x\right)-{\delta }_y\left(y\right)+{\delta }_y\left(z\right)-x{\epsilon }_z\left(y\right)-z{\epsilon }_x\left(x\right)+z{\epsilon }_x\left(y\right)-z{S}_y\left(z\right)\\ \Delta z_s={\delta }_z\left(x\right)-{\delta }_z\left(y\right)+{\delta }_z\left(z\right)+x{\epsilon }_y\left(y\right)+y{\epsilon }_x\left(y\right)\end{array}$ (2)

式中， ${\delta }_m\left(n\right)$ 、 ${\epsilon }_m\left(n\right)\left(m=x,y,z,n=x,y,z\right)$ 分别为n轴m方向的线误差和角误差， $S_m\left(n\right)\left(m=x,y,z,n=x,y,z\right)$ 为垂直度误差。

3. 基于球杆仪圆轨迹的空间误差模型验证

根据空间内两点间距离公式，球杆仪杆长变化量和空间误差变化量之间的关系为：

$\Delta r=\sqrt{{\left(x+\Delta x_a-\Delta x_0\right)}^2+{\left(y+\Delta y_a-\Delta y_0\right)}^2+{\left(z+\Delta z_a-\Delta z_0\right)}^2}-r$ (3)

式中， $\Delta x_a$ 、 $\Delta y_a$ 、 $\Delta z_a$ 和 $\Delta x_0$ 、 $\Delta y_0$ 、 $\Delta z_0$ 分别表示圆弧上任意一点a和圆心o的X、Y、Z方向上的偏离误差。

根据空间误差模型对球杆仪圆轨迹进行预测，验证误差模型，流程如图3所示。

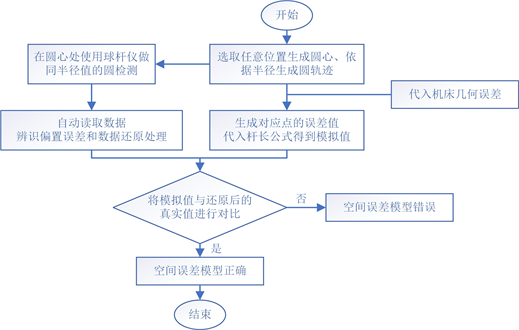
Figure 3. Error prediction flow based on arc trajectory

图3. 基于圆弧轨迹的误差预测流程

4. 球杆仪中心偏置误差的去除

4.1. 基于三角函数的偏置误差分析

以XOY平面圆检测为例，设圆轨迹误差检测中，底座对中时存在水平方向大小为u和竖直方向大小为v的偏差量，AQ是模拟存在中心偏置下测得的半径值，如图4所示。对于圆上任意一点(x, y)的球杆仪的杆长量可以用下式表示：

${\left(x-u\right)}^2+{\left(y-v\right)}^2={\left(AQ\right)}^2$ (1)

圆轨迹上任意一点与对应检测角度 $\theta$ 的关系式如下：

$\{\begin{array}{l}{x}^2+y^2=r^2\\ \cos \theta =x/r\\ \sin \theta =y/r\end{array}$ (5)

忽略掉 $u^2$ 和 $v^2$ 这一部分高阶小量，上式可以化简为：

$u\cos \theta +v\sin \theta =\frac{AQ+r}{-2r}\left(AQ-r\right)$ (6)

式中， $AQ-r$ 为球杆仪测得的半径变化量， $\frac{AQ+r}{-2r}\approx -1$。

即：

$-u\cos \theta -v\sin \theta =\Delta r^{\prime }$ (7)

式中， $\Delta r^{\prime }$ 表示存有偏置误差下的杆长变化量。

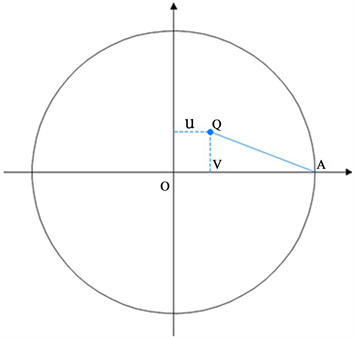
Figure 4. Schematic diagram of bias error

图4. 偏置误差示意图

4.2. 偏置误差仿真分析

本文基于三角函数拟合的方法，去除检测中存在的偏置误差。由于机床误差与偏置误差的耦合特性，将该方法的验证分为(a)和(b)两部分进行。

(a) 仅存在偏置误差下的仿真试验

仅存在偏置误差u，v时，设检测的半径为100 mm，采样的点数为360个，检测圆弧的角度为2π，根据球杆仪的检测原理，在MATLAB中计算得到对应的检测角度与半径变化量的数据，根据式(7)得：

$\Delta r^{\prime }=P\cdot C$ (8)

式中：

$P=\left[\begin{array}{cc}-\cos {\theta }_1& -\sin {\theta }_1\\ ⋮& ⋮\\ -\cos {\theta }_i& -\sin {\theta }_i\\ ⋮& ⋮\\ -\cos {\theta }_n& -\sin {\theta }_n\end{array}\right]n=360,C=\left[\begin{array}{c}u\\ v\end{array}\right]$

用最小二乘法对u和v进行求解，得到偏置误差的估计值。

$\left[\begin{array}{c}\hat{u}\\ \hat{v}\end{array}\right]={\left[P^{\text{T}}P\right]}^{-1}{P}^{\text{T}}\Delta r^{\prime }$ (9)

根据仅存在偏置误差下的仿真试验的辨识结果，辨识得到的偏差值与预设值完全一致，说明基于三角函数下的偏置误差辨识方法准确。

(b) 同时存在几何误差和偏置误差下的仿真试验

在球杆仪模拟器中添加中心偏置误差，并添加部分几何误差，参数如表1所示。

Table 1. Geometry error parameter settings of simulator

表1. 模拟器中的几何误差参数设置

经过三角函数方法的辨识后，得到中心偏置X的值为25.37 mm，中心偏置Y的值为−11.78 mm，辨识的准确率分别为98.52%和98.17%，证明基于三角函数的偏置误差辨识方法有效。依据下式将球杆仪数据还原：

$\{\begin{array}{l}\Delta r=\sqrt{\left(x^{\prime }+u\right)+\left(y^{\prime }+u\right)}-r\\ x^{\prime }=\left(r+\Delta r\right)\cos \theta \\ y^{\prime }=\left(r+\Delta r\right)\sin \theta \end{array}$ (10)

式中， $\Delta r$ 表示去除偏置误差的杆长变化量。

在球杆仪提供的模拟器中，将检测数据与还原后的数据进行比对，如图5(a)所示。在图5(b)中，曲线A表示基于三角函数法去除偏置误差后的数据；曲线B表示含几何误差但不含偏置误差的数据；曲线C表示设置了与B相同的几何误差同时含偏置误差的数据。

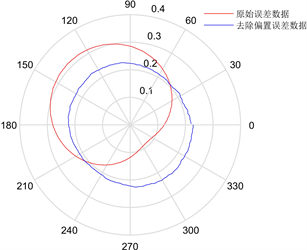(a) 极坐标 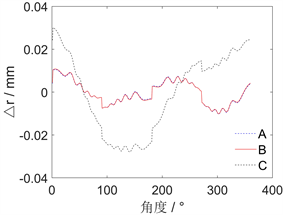(b) 直角坐标

Figure 5. De-bias the comparison of the results

图5. 去偏置结果对比

可以看出，曲线AB重合，曲线C波动较大，引入的偏置误差对球杆仪检测的数据具有较大的影响。此外，偏置误差一般较大，往往会覆盖掉几何误差对杆长变化量的影响，增加了分析几何误差的难度，所提的三角函数法能有效地除去偏置误差。

5. 实验验证

使用RenishawQC-20 W无线球杆系统(分辨率：0.1 μm)在TC-E650型五轴机床上进行XOY平面的误差检测实验，将误差模型得到的杆长变化量模拟值与球杆仪测得的实际值进行比对。实际情况下，球杆仪采集得到的数据较多，根据实测圆上的数据数量对角度进行均分，以线性插值的方法均匀生成360个点的真实杆长值，最终得到的预测轨迹与实际轨迹对比如图6所示。

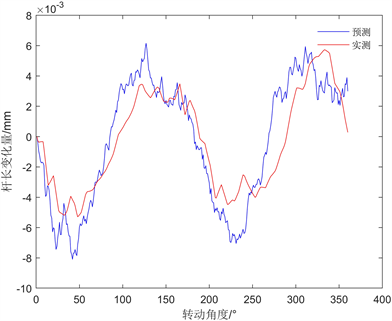(a) 直角坐标 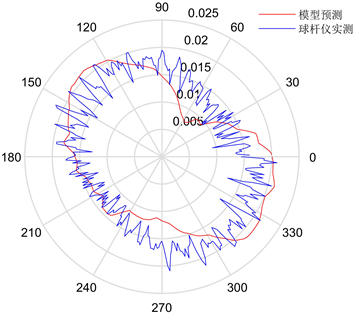(b) 极坐标

Figure 6. Comparison between measured and predicted results of arc trajectory

图6. 圆弧轨迹测量与预测对比

由图6可以得到，基于空间误差模型的球杆仪轨迹误差预测与实际测量值具有较好的一致性，总体结果趋势一致且比较吻合。虽然预测值在峰值处误差偏差量较大，可能导致的原因在于实际圆检测中，机床运动轴在换向的过程中引入的误差量较多，如反向间隙、反向越冲、摩擦等，会对误差圆轨迹预测的准确性造成较大的影响。对于整体的误差预测而言，其最大的残差为−6.7 mm，经过预测后，理论上经过预测后圆度误差与测量值基本吻合，误差值为4.2%。

6. 结论

本文分析了偏置误差对球杆仪杆长的影响，提出了基于三角函数的偏置误差消除方法，分别对仅存在偏置误差的情况和几何误差与偏置误差耦合的情况进行了仿真分析，结果表明，偏置误差对几何误差影响较大，三角函数法去除偏置误差准确有效；构建了基于多体系统理论的五轴机床平动轴误差模型，通过该模型对机床联动所产生的圆弧轨迹进行了误差预测，以TC-E650型五轴机床为对象，进行了球杆仪圆轨迹实测，实验表明，基于模型预测后的圆度与实测圆度偏差仅为4.2%，所提圆轨迹预测方法有效。