基于属性加权的独依赖条件概率编码方法

doi:10.12677/ORF.2023.131009

期刊菜单

基于属性加权的独依赖条件概率编码方法
One Dependence Conditional Probability Encoding Method Based on Attribute Weighting

DOI: 10.12677/ORF.2023.131009, PDF, HTML, XML, 国家自然科学基金支持
作者: 梁祖鹏：贵州大学数学与统计学院，贵州贵阳；李秋德^*, 胡思贵：贵州医科大学生物与工程学院，贵州贵阳
关键词: 混合数据分类；条件概率编码；独依赖值差度量；属性加权；Mixed Data Classification； Conditional Probability Encoding； One Dependence Value Difference Metric； Attribute Weighting

摘要: 包含分类属性和数值属性的混合数据广泛存在于真实世界采集的数据或实验数据，在挖掘或分析这类数据前，通常需要将它们处理(转换/嵌入/表示/编码)为高质量的数值数据。条件概率编码方法(以属性条件独立假设为前提)在大多数情况下能取得不错的性能，但当它面对具有强属性关联的数据集时，性能并不理想。受独依赖值差度量的启发，将放宽属性条件独立的构想应用于条件概率编码方法。此外，还利用属性加权法来优化编码后的数据质量。融合上述这些方法，我们为混合数据的分类编码提出了一个属性加权的独依赖条件概率编码方法。实验结果表明，我们的编码方法可以显著性提高数据转换的质量，从而增强后续数据分析算法的性能。

Abstract: Mixed data containing categorical and numerical attributes are widely available in real-world or experimental data sets. Before mining or analyzing such data, it is typically necessary to process (transform/embed/represent) them into high-quality numerical data. Conditional probability transformation method (which is premised on the attribute conditional independence assumption) can provide acceptable performance in the majority of cases, but it is not satisfactory for data sets with strong attribute association. Inspired by the one dependence value difference metric method, the concept of relaxing the attributes conditional independence is applied to the conditional probability transformation method. In addition, an attribute weighting method is designed to optimize the quality of data encoding. Combining these methods, we propose an Attribute Weighted One Dependence Conditional Probability Encoding method for categorical encoding on mixed data. Extensive experimental results demonstrate that our method can significantly boost the quality of data encoding, hence enhancing the performance of subsequent data analysis algorithms.

文章引用：梁祖鹏, 李秋德, 胡思贵. 基于属性加权的独依赖条件概率编码方法[J]. 运筹与模糊学, 2023, 13(1): 74-87. https://doi.org/10.12677/ORF.2023.131009

1. 引言

在实际工作中收集的数据，由于收集方式和数据来源的不同，这些数据通常包含数值型、分类型、多媒体等多种类型，这给挖掘出有价值的信息时带来了挑战 [1]。为解决数据类型多样化问题，通过数据预处理，将原始数据编码为分类型、数值型或混合型数据(包括数值型和分类型)，然后再应用于机器学习算法进一步开展数据挖掘任务 [2]。就我们所知，很多高性能的机器学习算法只能处理单一的数据类型(即分类型或数值型)，例如，神经网络和回归等算法只能输入数值型数据，决策树和朴素贝叶斯等算法只能应用于分类型数据。但是这些机器学习算法中只有少数可以直接处理分类数据，并且数值数据比分类数据有更好的代数特性。因此，为了将混合数据广泛应用于支持数值输入的机器学习算法，在混合数据中把分类数据转化为数字数据是一种常见的方式 [3]。

然而，如果编码过程损失过多的信息，将得到低质量的数值数据，这会严重影响后续学习算法的性能和可靠性 [4]，因此，寻找一种高质量的编码方法至关重要，如何将混合型数据编码为高质量的单一数据类型吸引了研究者的广泛关注 [5]。Kasif等人 [6] 提出了能够处理分类型数据的MBR转换(或称为条件概率转换，CPT)，它在分类数据的距离度量(如值差度量 [7] )中取得了不错的性能。此外，我们针对CPT的不足，试图寻找对应的缓解策略。CPT是以条件独立性假设为前提，当数据的属性之间存在强相关关系时，该方法估计的条件概率是不准确的。为此，学者们提出了一系列的改进方法。Jiang等人 [8] 提出了隐藏朴素贝叶斯模型，它通过为每一个属性构造隐藏父属性改进条件概率公式，从而放松属性之间的条件独立性假设；Li等人 [8] 通过微调条件概率的方法提出了一个微调条件概率转换；Li等人 [9] 通过引入TAN-tree放宽条件独立性假设以改进条件概率，提出独依赖值差度量(ODVDM)。

此外，在实证研究中我们发现：转换后的数据集中，属性加权对数据挖掘起着重要作用，为此，需要设计一种适合于数据的属性加权方法。Zhang等人 [10] 提出属性和实例加权的朴素贝叶斯(AIWNB)，它结合实例加权和属性加权，对于属性权重定义为互相关性和平均互关联度的差值，利用标准sigmod函数处理属性权重并加权 [11]。Wang等人 [12] 提出双重加权的平均独依赖估计(DWAODE)，他们用属性加权和模型加权对平均独依赖估计器(AODE)进行优化，注意到以不同超父属性结点的超父独依赖估计器(SPODE)性能不同，对AODE中的每一个SPODE赋予一个权重，并且对SPODE中的每一个属性加权，两者结合后的模型可以提升准确性。Zhang等 [5] 提出多传递距离嵌入学习(MTDLE)，这也是一种混合数据分类属性转换方法，它通过多传递距离学习得到任意两个样本之间的距离矩阵，再通过必连与勿连约束得到对应样本距离矩阵的权重并加权，作为最后的转换结果。以上运用属性加权方法都可以提升模型的性能，说明属性加权是有效的。因此，我们通过借鉴ODVDM和属性加权的构想，提出了一个属性加权的独依赖条件概率编码方法(AWODCPE)，改进CPT以提高它的分类数据编码质量。

本文的组织结构如下。第2节介绍了一些预备知识，包括混合数据集介绍、条件概率转换方法、TAN-tree和属性加权方法的主要内容。第3节介绍属性加权的独依赖条件概率编码方法的主要内容。第4节设计实验来证明我们方法的数据编码性能。最后在第5节总结。

2. 预备知识

2.1. 混合数据集

混合数据集是指包含分类属性和数值属性的结构化数据集，如表1 (“Automobile”数据集所示)。其中，“engine type”、“aspiration”和“fuel-type”是分类属性，“width”、“horsepower”是数值属性，“class”为分类标签。

Table 1. Description of mixed datasets

表1. 混合数据集介绍

2.2. 条件概率转换方法

令 $X = {x_{i}}_{i = 1}^{N}$ 是一个混合数据集， $M (= M_{c} + M_{n})$ 是所有属性 $A = {A_{j}^{c}}_{j = 1}^{M_{c}} \cup {A_{j}^{n}}_{j = M_{c} + 1}^{M}$ 的总数，这里 ${A_{j}^{c}}_{j = 1}^{M_{c}}$ 和 ${A_{j}^{n}}_{j = M_{c} + 1}^{M}$ 分别是 $M_{c}$ 个分类属性和 $M_{n}$ 个数值属性。数值属性可表示为：

$A_{j}^{n} \to {[x_{1, j}^{(n)}, \dots, x_{N, j}^{(n)}]}^{T}, j = M_{c} + 1, \dots, M$ (1)

这里 $x_{i, j}^{(n)}$ 是第i个实例第j个数值属性的属性值，其中 $i = 1, \dots, N; j = 1, \dots, M_{c}$ 。同理分类属性可表示为

$A_{j}^{c} \to {[x_{1, j}^{(c)}, \dots, x_{N, j}^{(c)}]}^{T}, j = 1, 2, \dots, M_{c}$ (2)

这里 $x_{i, j}^{(c)}$ 是第i个实例第j个分类属性的属性值。CPT将分类属性值 $x_{i, j}^{(c)}$ 转换为数值行向量 $a_{j} (x_{i}^{(c)})$ ：

$x_{i, j}^{(c)} \to a_{j} {(x_{i}^{(c)})}_{1 \times l} = {[P (c_{1} | x_{i, j}^{(c)}), P (c_{2} | x_{i, j}^{(c)}), \dots, P (c_{l} | x_{i, j}^{(c)})]}_{1 \times l}$ (3)

其中， $P (c_{l} | x_{i, j}^{(c)}) = \frac{\sum_{t = 1}^{N} δ (x_{t, j}^{(c)}, x_{i, j}^{(c)}) δ (c_{i}, c_{t}) + 1}{\sum_{t = 1}^{N} δ (x_{t, j}^{(c)}, x_{i, j}^{(c)}) + l}$ ，这里l是标签个数， $P (c_{l} | x_{i, j}^{(c)})$ 是给定标签 $c_{l}$ 属性值 $x_{i, j}^{(c)}$ 的概率。由公式(3)可知，CPT是以属性条件独立性假设为前提，然而在所有的属性之间可能存在依赖关系，例如表1中“engine type”和“aspiration”或“fuel-type”之间存在联系，如果忽略这种依赖关系可能会导致估计的概率不准确 [9]。

2.3. TAN-tree

独依赖值差度量 [9] 实行与贝叶斯分类器 [13] 相同的策略学习属性之间的网络结构，生成一棵TAN-tree以获得不同属性的依赖关系，具体步骤如下：

1) 使用下式计算任意两个分类属性之间的条件互信息

$I (x_{i, j}^{(c)}, x_{i, k}^{(c)} | c) = \sum_{x_{i, j}^{(c)}, x_{i, k}^{(c)}; c \in y} P (x_{i, j}^{(c)}, x_{i, k}^{(c)} | c) \log \frac{P (x_{i, j}^{(c)}, x_{i, k}^{(c)} | c)}{P (x_{i, j}^{(c)} | c) P (x_{i, k}^{(c)} | c)}$ ； (4)

2) 以属性为结点构建完全图，将图中任意两个结点之间无向边的权重设为 $I (x_{i, j}^{(c)}, x_{i, k}^{(c)} | c)$ ；

3) 构建完全图的最大带权生成树，挑选根变量，将边设置为有向；

4) 加入标签结点c，增加从c到每个属性的有向边。

2.4. 属性加权方法

属性加权 [14] 为0到1之间的每个属性分配连续的权重。在AIWNB [10] 中，通过以下公式计算权重，首先计算属性与标签之间和属性与属性之间的条件互信息：

$I (A_{j}; C) = \sum_{x_{i, j}^{(c)} \in A_{j}} \sum_{c \in C} P (x_{i, j}^{(c)}, c) \log \frac{P (x_{i, j}^{(c)}, c)}{P (x_{i, j}^{(c)}) P (c)}$ (5)

$I (A_{j}; A_{k}) = \sum_{x_{i, j}^{(c)} \in A_{j}} \sum_{x_{i, k}^{(c)} \in A_{k}} P (x_{i, j}^{(c)}, x_{i, k}^{(c)}) \log \frac{P (x_{i, j}^{(c)}, x_{i, k}^{(c)})}{P (x_{i, j}^{(c)}) P (x_{i, k}^{(c)})}$ (6)

再将公式(5)和公式(6)的条件互信息归一化：

$N I (A_{j}; C) = \frac{I (A_{j}; C)}{\frac{1}{m} \sum_{j = 1}^{m} I (A_{j}; C)}$ (7)

$N I (A_{j}; C) = \frac{I (A_{j}; A_{k})}{\frac{1}{m (m - 1)} \sum_{j = 1}^{m} \sum_{k = 1 \land k \neq j}^{m} I (A_{j}; A_{k})}$ (8)

最后由属性权重定义为互相关性和平均互关联度的差值(即公式(9))，并利用sigmoid函数将权重映射到[0, 1]中(即公式(10))：

$Δ w_{j}^{a t t} = \underset{互相关性}{\underset{︸}{N I (A_{j}; C)}} - \underset{平均互关联度}{\underset{︸}{\frac{1}{m - 1} \sum_{j = 1}^{m} \sum_{k = 1 \land k \neq j}^{m} N I (A_{j}; A_{k})}}$ (9)

$w_{j}^{a t t} = \frac{1}{1 + e^{- Δ w_{j}^{a t t}}}$ (10)

AIWNB [10] 中的实验证明属性加权确实取得了不错的效果，每个属性的权重被纳入到公式(11)所示的朴素贝叶斯分类公式中：

$c (x_{i}) = \arg \max_{c \in C} P (c) \prod_{j = 1}^{m} P {(x_{i, j}^{(c)} | c)}^{w_{j}^{a t t}}$ (11)

上式中， $P (c)$ 是标签为c时的先验概率， $P (x_{i, j}^{(c)} | c)$ 是标签为c时分类属性值为 $x_{i, j}^{(c)}$ 的条件概率。除了上述的加权方式，在MTDLE中，通过判别嵌入的方法为不同共现行为得到的距离矩阵加权，具体用公式(12)为距离矩阵加权：

$D = \sum_{j = 1}^{n} w_{j} D_{j}$ (12)

上式中，D_j是由不同共现行为得到的距离矩阵，D是加权后的距离矩阵。而我们的方法借鉴MTDLE的加权方式为转换后的数据加权。因此，我们结合独依赖值差度量放松属性依赖性的方法和属性加权对条件概率编码进行改进，提出属性加权的独依赖条件概率编码方法(AWODCPE)。

3. 属性加权的独依赖条件概率编码方法

3.1. 算法框架

AWODCPE具体的编码过程分为两个部分：

Figure 1. AWODCPE framework

图1. AWODCPE框架

根据图1第一部分提出了一个独依赖条件概率编码方法，将混合属性数据中的分类数据转换为数值数据。首先，计算每个数据集所有分类属性之间的TAN-tree得到分类属性之间的依赖性，改进CPT的公式，将一个分类属性值转换成一条条件概率向量，并替换原分类属性 $A_{j}^{c}$ 中对应的分类属性值得到数值属性 ${A^{'}}_{j}$ ，以此提高混合数据的转换质量。

第二部分是基于属性之间的条件互信息的属性加权方法。由于公式(6)和公式(8)中没有考虑标签对属性与属性之间条件互信息的影响，所有我们对这两个公式进行改进，求出每个数据集的所有分类属性的权重之后并加权，表示为：

$w_{1} {A^{'}}_{1}, w_{2} {A^{'}}_{2}, \dots, w_{M_{c}} {A^{'}}_{M_{c}}$ (13)

3.2. 独依赖条件概率编码

由前面所述，CPT具有现实中不成立的条件独立性假设，因此，我们使用独依赖值差度量相同的方法进行改进。经过计算TAN-tree的四个步骤，我们能够获得每个数据集中分类属性依赖关系，但仅保留了最相关属性之间的依赖性，并没有包括所有的分类属性信息。我们从TAN-tree中得到除根结点之外所有分类属性的父属性之后，再将分类属性值 $x_{i, j}^{(c)}$ 转换成数值向量 $a_{j} (x_{i}^{(c)})$ ：

$\begin{array}{l} x_{i, j}^{(c)} \to a_{j} {(x_{i}^{(c)})}_{1 \times (l \cdot n_{j p})} \\ = {([P (c_{1} | x_{i, j}^{(c)}, x_{1, j p}^{(c)}), \dots, P (c_{l} | x_{i, j}^{(c)}, x_{1, j p}^{(c)})], \dots, [P (c_{1} | x_{i, j}^{(c)}, x_{n_{j p}, j p}^{(c)}), \dots, P (c_{l} | x_{i, j}^{(c)}, x_{n_{j p}, j p}^{(c)})])}_{1 \times (l \cdot n_{j p})} \end{array}$ (14)

上式中 $n_{j p}$ 为父属性 $A_{j p}$ 的属性值个数，则第j个分类属性值可转换成

${A^{'}}_{j} \to {[a_{j} (x_{1}^{(c)}), a_{j} (x_{2}^{(c)}), \dots, a_{j} (x_{N}^{(c)})]}_{N \times (l \cdot n_{j p})}^{T}$ (15)

其中， $P (c_{l} | x_{i, j}^{(c)}, x_{i, j p}^{(c)}) = \frac{\sum_{t = 1}^{N} δ (x_{t, j}^{(c)}, x_{i, j}^{(c)}) δ (x_{t, j p}^{(c)}, x_{i, j p}^{(c)}) δ (c_{i}, c_{t}) + 1}{\sum_{t = 1}^{N} δ (x_{t, j}^{(c)}, x_{i, j}^{(c)}) δ (x_{t, j p}^{(c)}, x_{i, j p}^{(c)}) + l}$ ，式中l是标签个数， $δ (\cdot)$ 是示性函数(当函

数中的两个元素相等时，返回1，否则返回0)， $x_{i, j p}^{(c)}$ 是第j个属性 $A_{j}$ 的父属性 $A_{j p}$ 同一行的属性值， $P (c_{l} | x_{i, j}^{(c)}, x_{i, j p}^{(c)})$ 是给定标签 $c_{l}$ 和父属性值 $x_{i, j p}^{(c)}$ 的 $x_{i, j}^{(c)}$ 的概率。通过公式(14)和公式(15)，我们就能将分类属性转换为数值属性。

3.3. 属性加权

因为不同的属性的重要性不同，需要为其分配权重并加权。我们借鉴AIWNB [10] 的方法计算权重，但是他们的公式(6)中没有考虑标签的信息，这可能导致计算权重时出现偏差。在DWAODE [12] 中，他们通过使用属性与标签之间的条件概率计算条件互信息，我们借鉴他们的方法改进AIWNB的权重计算公式(6)。对公式改进如下：

$I (A_{j}; A_{k} | C) = \sum_{x_{i, j}^{(c)} \in A_{j}} \sum_{x_{i, k}^{(c)} \in A_{k}} \sum_{c \in C} P (x_{i, j}^{(c)}, x_{i, k}^{(c)} | c) \log \frac{P (x_{i, j}^{(c)}, x_{i, k}^{(c)} | c)}{P (x_{i, j}^{(c)} | c) P (x_{i, k}^{(c)} | c)}$ (16)

其中，

$P (x_{i, j}^{(c)} | c) = \frac{P (x_{i, j}^{(c)}, c)}{P (c)}$ (17)

$P (x_{i, k}^{(c)} | c) = \frac{P (x_{i, k}^{(c)}, c)}{P (c)}$ (18)

$P (x_{i, j}^{(c)}, x_{i, k}^{(c)} | c) = \frac{P (x_{i, j}^{(c)}, x_{i, k}^{(c)}, c)}{P (c)}$ (19)

公式(17)(18)(19)中的概率又由以下四个公式计算：

$P (c) = \frac{\sum_{t = 1}^{N} δ (c_{t}, c) + 1 / q}{N + 1}$ (20)

$P (x_{i, j}^{(c)}, c) = \frac{\sum_{t = 1}^{N} δ (x_{t, j}^{(c)}, x_{i, j}^{(c)}) δ (c_{t}, c) + 1 / (n_{j} \cdot q)}{N + 1}$ (21)

$P (x_{i, k}^{(c)}, c) = \frac{\sum_{t = 1}^{N} δ (x_{t, k}^{(c)}, x_{i, k}^{(c)}) δ (c_{t}, c) + 1 / (n_{k} \cdot q)}{N + 1}$ (22)

$P (x_{i, j}^{(c)}, x_{i, k}^{(c)}, c) = \frac{\sum_{t = 1}^{N} δ (x_{t, j}^{(c)}, x_{i, j}^{(c)}) δ (x_{t, k}^{(c)}, x_{i, k}^{(c)}) δ (c_{t}, c) + 1 / (n_{j} \cdot n_{k} \cdot q)}{N + 1}$ (23)

这里q是标签数量， $n_{j}$ 和 $n_{k}$ 分别是是第j个和第k个分类属性中属性值的数量，N是实例个数。由以上四个公式计算出任意两个属性之间给定标签情况下的条件信息值后，我们归一化条件互信息：

$N I (A_{j}; C) = \frac{I (A_{j}; C)}{\frac{1}{m} \sum_{j = 1}^{m} I (A_{j}; C)}$ (24)

$N I (A_{j}; A_{k} | C) = \frac{I (A_{j}; A_{k} | C)}{\frac{1}{m (m - 1)} \sum_{j = 1}^{m} \sum_{k = 1 \land k \neq j}^{m} I (A_{j}; A_{k} | C)}$ (25)

公式(9)可变为：

$Δ w_{j} = N I (A_{j}; C) - \frac{1}{m - 1} \sum_{j = 1}^{m} \sum_{k = 1 \land k \neq j}^{m} N I (A_{j}; A_{k} | C)$ (26)

然而，通过公式(26)计算的权重可能为负，所以我们通过公式(10)将权重映射在区间[0, 1]中，得到分类属性的M_c个权重： $w_{1}, w_{2}, \dots, w_{M_{c}}$ ，并对编码后的分类属性 ${A^{'}}_{1}, {A^{'}}_{2}, \dots, {A^{'}}_{M_{c}}$ 加权，可表示为：

$w_{1} {A^{'}}_{1}, w_{2} {A^{'}}_{2}, \dots, w_{M_{c}} {A^{'}}_{M_{c}}$ (27)

原始的数值数据不做任何处理，并与式(27)的数据拼接获得最后的转换数据：

$w_{1} {A^{'}}_{1}, \dots, w_{M_{c}} {A^{'}}_{M_{c}}, A_{M_{c} + 1}^{n}, \dots, A_{M}^{n}$ (28)

3.4. 算法设计与时间复杂度分析

我们的数据编码算法设计见表2，对于Algorithm 1的时间复杂度如下：步骤1和步骤8至步骤12中计算考虑标签后的任意两个属性之间的条件互信息值花费时间按复杂度为 $O (c n_{j} n_{k} M_{c}^{2})$ (这里c是标签数量， $M_{c}$ 是类别属性数量，n_j和n_k分别是第j个分类属性的属性数量和第k个分类属性的属性数量)；步骤2至步骤6计算每个属性对应的概率向量，时间复杂度为 $O (c n_{j} n_{j p} M_{c})$ (这里n_jp是第j个分类属性的父属性属性值数量)。

4. 实验设计和评估

4.1. 实验设置

4.1.1. 参数设置

在我们的实验中，我们使用多重感知机分类器 [15] (Multilayer Perceptron, MLP)评估后续数据转换学习算法的质量，构造一层隐藏层，最大迭代次数(max iter)设置为1000，激活函数为“relu”函数。

Table 2. Algorithm design

表2. 算法设计

本节给出的所有实验都是在Intel(R) Core(TM) i5-10500 CPU @ 3.10GHz 3.10GHz处理器上执行的，内存为8GB，在Windows 10 Professional x64上运行。MLP和22个编码方法是从scikit-learn的程序包中调用的，scikit-learn是一个广泛使用的用Python实现的机器学习库。实验在Python 3.10环境下运行。

4.1.2. 数据集和预处理

我们基于以下原因使用来自加州大学机器学习领域UCI数据库的18个数据集：1) 这些数据集的样本实例数量差距较大，方便我们比较方法之间的转换效率；2) 它们包括两种属性，即分类属性和数值属性；3) 它们来源广泛，比如医学和商业等。

我们对这些数据集有如下处理：1) 缺失值替换处理，数值属性用平均值替换缺失值，分类属性用出现次数最多的属性值替换缺失值；2) 删除数据集中的重复对象；3) 移除属性值太多或因数据缺失导致只有一个属性值的无用属性(比如“Zoo”数据集中的属性“animal”有100个以上的属性值，“Anneal”数据集中的“exptl”和“ferro”属性只有一个属性值)。我们将经过以上处理后的18个数据集信息总结在表中(见表3)。

Table 3. Description of 18 UCI datasets used in the experiments

表3. 实验中18个UCI数据集介绍

4.1.3. 评估标准

我们使用20折交叉验证的F1得分 [16] 对实验结果的性能进行评价，并在每个单元格中标出平均值 ±标准差，使用置信水平为0.95的双尾t检验 [17] 在统计意义上比较在所有数据集上所有方法之间的显著性差异，并且单元格中的○和●的意义分别是我们的方法与对比方法相比在统计学意义上有显著的退化和改善。每个数据集最好的F1得分加粗。表底部还总结了在所有数据集上的平均值(average)，最优F1得分(# of best)，Win/Tie/Loss (W/T/L)和平均序值(AR)。W/T/L意义是我们的方法与对比方法相比，赢W个数据集，平T个数据集，输L个数据集。我们还使用箱线图总结F1-score，每个箱体中的直线是该方法的中位线，并且将我们的方法(AWODCPE)的中位线用红色虚线延伸，并标出数值，直观地确定方法的优缺点。

除了以上评估方法之外，我们为了进一步分析AWODCPE在多个数据集上的泛化性能，使用Friedman 检验及其后续Nemenyi检验的统计假设检验 [18]。在使用Friedman检验时， $X_{F}^{2}$ 对应的分布服从自由度为 $k - 1$ 和 $(k - 1) (N_{d} - 1)$ 的F分布(这里k是算法个数， $N_{d}$ 是数据集个数)。若在95%显著性水平下， $X_{F}^{2}$ 值大于对应F分布临界值，则拒绝原假设，表明不同方法之间有显著性差异。最后，我们使用后验Nemenyi检验直观的确定方法之间是否有显著差异。在p值小于0.05时，Nemenyi检验的平均序值差别的临界值为：

$C D = q_{α} \sqrt{\frac{k (k + 1)}{6 N_{d}}}$ (29)

其中 $q_{α}$ 为Tukey分布的临界值。

4.2. 编码算法性能评估

我们从scikit-learn的Category Encoder库中选出4种编码方法与CPT和AWODCPE比较数据编码性能，这4种编码方法如下：

· Ordinal Encoder：顺序编码将分类属性值映射为连续的整数值。

· Target Encoder [19]：由Micci等人于2001年提出，使用参数函数作为加权因子计算对应的数值标签均值和总标签均值的加权平均值作为最后的数值估计。

· Catboost Encoder [20]：由Prokhorenkova等人于2018年提出，计算当前所在行的标签平均值与总标签数之比，并使用先验概率进行平滑处理，处理后的值作为最后的数值估计。

· Quatile Encoder [21]：由Mougan等人于2021年提出，利用对应属性的样本数和正则化参数定义权重，对具有相同标签的样本的p分位数和全局p分位数进行加权，加权后的值作为最后的数值估计。

AWODCPE与以上6种方法的比较结果被总结在表4、图2和图3中，我们将重点做如下总结：

1) 在表4中，AWODCPE的平均的F1得分是最高的(86.87%)，与CPT(84.92%)相比高1.95%。我们的方法比其它4种方法高至少3%。我们方法的最高成绩数为12个，远高于其它比较方法。在统计学意义上，我们方法与CPT相比，赢7个数据集，平10个数据集，输1个数据集，明显优于CPT，并且也显著由于其它4个方法。平均排序为1.72在所有方法中最小，仅以平均排序来看CPT与AWODCPE的差距最小。

2) 从图2中可以看出，AWODCPE的箱体上下限差距最小区别于其它5种方法，这说明我们的方法有更优秀的稳定性。并且我们的方法比其他方法有更高的箱体位置和中位线，说明拥有更好的转换性能。

3) 在95%显著性水平下，Friedman检验的大于临界值 $F_{0.95} (5, 85) (= 2.32)$ ，说明各方法之间有显著区别。因此，我们计算CD值为1.78，并以表4中的平均排序(AR)为基础，在图3中直观表现各个编码方法之间的区别。可以看出AWODCPE最佳，各方法之间有显著性差异，显著优于Ordinal、Target、catboost和Quatile。

Table 4. F1-score comparisons for our method versus 6 encoding methods

表4. 我们的方法与6个编码方法的F1得分比较

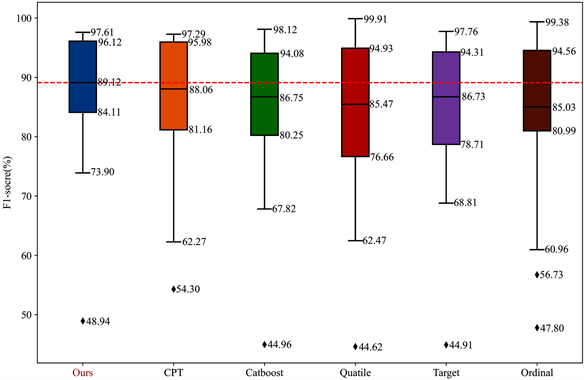
Figure 2. Comparison of AWODCPE with its competitors in terms of F1-score

图2. 我们的方法与竞争者在F1得分方面的比较

Figure 3. F1-score comparison of our method versus its competitors per Nemenyi test

图3. 根据Nemenyi检验，我们的方法与竞争者的F1得分比较

4.3. 时间开销评估

我们将本节实验中，将转换后的数据集输入多重感知机分类器，记录分类器在这些数据集上的时间花费，并结果总结在了表5中。同样地，每个数据集最好的时间花费加粗。从表中可以看出，我们的方法由于维度扩张造成在“census”数据集上的时间花费远高于其他方法，导致拉高了平均值。在其他数据集上，比其他方法的花间花费稍高。

进一步地，我们在95%显著性水平下，计算Friedman检验的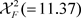大于临界值 $F_{0.95} (5, 85) (= 2.32)$ ，说明各方法之间有显著区别。因此，我们计算CD值为1.78。同样地，根据表5中的平均排序(AR)画出图4。从图中可以看出，我们方法的时间开销不算理想，但在转换性能和时间成本的权衡之下，是可以接受的。

Table 5. F1-score comparisons for our method versus 6 encoding methods

表5. 我们的方法与6个编码方法的F1得分比较

Figure 4. Time Cost comparison of our method versus its competitors per Nemenyi test

图4. 根据Nemenyi检验，我们的方法与竞争者的时间花费比较

5. 结论

为了将混合数据应用于数值输入的机器学习算法，需要将分类属性数据转换为数值属性数据，而如何高质量地完成转换，这对于学者们是一大挑战。对于这个问题，本文提出了一种属性加权的独依赖条件概率编码算法(AWODCPE)。它通过建立TAN-tree达到放松条件独立性假设的目的，通过放松后的依赖关系求出条件概率向量，再通过所有属性之间的条件互信息值求出每一个分类属性对应的权重并加权，得到最终的转换数据。在18个数据集上的实验说明了AWODCPE的转换性能比其它5个竞争者更优秀。

虽然AWODCPE从总体上已经取得了很好的效果，然而在如下的部分还可以做进一步改进。例如，在一个数据集中有些属性并不依赖于其他属性，然而为它赋予一个父属性后，可能会降低数据转换质量，所以我们可以寻找最先进的放松条件独立性假设的方法进行改进。或者是寻找一套求每个属性值权重的更有效的方法，从而降低转换过程的时间成本，使其具有更高的转换效率，这些都是我们将来的工作方向。

基金项目

本研究由国家自然科学基金(No. 62166009)、贵州省科技厅自然科学基金ZK [2021]333, ZK [2022]350资助；贵州省卫健委科学基金(No. gzwkj2023-258)、贵州医科大学博士研究启动基金(No. 2020-051)资助。

NOTES

^*通讯作者。

参考文献

[1]	Ramírez-Gallego, S., Krawczyk, B., García, S., Wozniak, M. and Herrera, F. (2017) A Survey on Data Preprocessing for Data Stream Mining: Current Status and Future Directions. Neurocomputing, 239, 39-57. https://doi.org/10.1016/j.neucom.2017.01.078
[2]	García, S., Luengo, J. and Herrera, F. (2015) Data Pre-processing in Data Mining. Intelligent Systems Reference Library. https://doi.org/10.1007/978-3-319-10247-4
[3]	Li, Q., Xiong, Q., Ji, S., Yu, Y., Wu, C. and Yi, H. (2021) A Method for Mixed Data Classification Base on RBF-ELM Network. Neurocomputing, 431, 7-22. https://doi.org/10.1016/j.neucom.2020.12.032
[4]	李秋德. 混合属性数据的处理及其分类算法研究[D]: [博士学位论文]. 重庆: 重庆大学, 2020. https://doi.org/10.27670/d.cnki.gcqdu.2020.000081
[5]	Zhang, K., Wang, Q., Chen, Z., Marsic, I., Kumar, V., Jiang, G. and Zhang, J. (2015) From Categorical to Numerical: Multiple Transitive Distance Learning and Em-bedding. Proceedings of the 2015 SIAM International Conference on Data Mining (SDM), Vancouver, 30 April-2 May 2015, 46-54. https://doi.org/10.1137/1.9781611974010.6
[6]	Kasif, S., Salzberg, S., Waltz, D. L., Rachlin, J. and Aha, D. W. (1998) A Probabilistic Framework for Memory-Based Reasoning. Artificial Intelligence, 104, 287-311. https://doi.org/10.1016/S0004-3702(98)00046-0
[7]	Stanfill, C. and Waltz, D. L. (1986) To-ward Memory-Based Reasoning. Communications of the ACM, 29, 1213-1228. https://doi.org/10.1145/7902.7906
[8]	Jiang, L., Zhang, H. and Cai, Z. (2009) A Novel Bayes Model: Hidden Naive Bayes. IEEE Transactions on Knowledge and Data Engineering, 21, 1361-1371. https://doi.org/10.1109/TKDE.2008.234
[9]	Li, C. and Li, H. (2011) One Dependence Value Difference Metric. Knowledge-Based Systems, 24, 589-594. https://doi.org/10.1016/j.knosys.2011.01.005
[10]	Zhang, H., Jiang, L. and Yu, L. (2021) Attribute and In-stance Weighted Naive Bayes. Pattern Recognition, 111, Article ID: 107674. https://doi.org/10.1016/j.patcog.2020.107674
[11]	Jiang, L., Zhang, L., Li, C. and Wu, J. (2019) A Correla-tion-Based Feature Weighting Filter for Naive Bayes. IEEE Transactions on Knowledge and Data Engineering, 31, 201-213. https://doi.org/10.1109/TKDE.2018.2836440
[12]	Wang, L., Xie, Y., Pang, M. and Wei, J. (2022) Alleviating the Attribute Conditional Independence and I.I.D. Assumptions of Averaged One-Dependence Estimator by Double Weighting. Knowledge-Based Systems, 250, Article ID: 109078. https://doi.org/10.1016/j.knosys.2022.109078
[13]	Friedman, N., Geiger, D. and Goldszmidt, M. (1997) Bayesian Network Classifiers. Machine Learning, 29, 131-163. https://doi.org/10.1023/A:1007465528199
[14]	Lee, C.-H. (2018) An Information-Theoretic Filter Approach for Value Weighted Classification Learning in Naive Bayes. Data & Knowledge Engineering, 113, 116-128. https://doi.org/10.1016/j.datak.2017.11.002
[15]	Popescu, M.-C., Balas, V., Perescu-Popescu, L. and Masto-rakis, N. (2009) Multilayer Perceptron and Neural Networks. WSEAS Transactions on Circuits and Systems, 8, 579-588.
[16]	Yang, C. C. (2010) Search Engines Information Retrieval in Practice. The Journal of the Association for Information Science and Technology, 61, 430. https://doi.org/10.1002/asi.21194
[17]	Nadeau, C. and Bengio, Y. (2003) Inference for the Generalization Error. Machine Learning, 52, 239-281. https://doi.org/10.1023/A:1024068626366
[18]	Demsar, J. (2006) Statistical Comparisons of Classifiers over Multiple Data Sets. Journal of Machine Learning Research, 7, 1-30.
[19]	Micci-Barreca, D. (2001) A Preprocessing Scheme for High-Cardinality Categorical Attributes in Classification and Prediction Problems. ACM SIGKDD Ex-plorations Newsletter, 3, 27-32. https://doi.org/10.1145/507533.507538
[20]	Prokhorenkova, L., Gusev, G., Vorobev, A., Dorogush, A.V. and Gulin, A. (2018) CatBoost: Unbiased Boosting with Categorical Features. Pro-ceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, 3-8 December 2018, 6639-6649.
[21]	Mougan, C., Masip, D., Nin, J. and Pujol, O. (2021) Quantile Encoder: Tackling High Car-dinality Categorical Features in Regression Problems. 18th International Conference, MDAI 2021, Umeå, 27-30 September 2021, 168-180. https://doi.org/10.1007/978-3-030-85529-1_14

为你推荐

友情链接