1. 引言
随着我国社会经济的高速发展,城市的高层建筑物、石油以及化工企业的数量得到大幅度的增加,可燃物品的种类非常多,这不可避免地存在着非常大的安全隐患问题。针对目前我国城市在新形势下的灭火救援任务所呈现出的特点,近些年提出了城市主战消防车的这一新型概念,所谓的城市主战消防车是指“执行救援灭火任务必须第一时间出动的具有多功能、高比功率、多乘员、高性能、短轴距、智能化等几大特征的消防车”,以满足日益复杂且多元化的社会需求 [1] [2] [3] 。城市主战消防车由于在大流量以及高压力的作业环境下工作必然会导致其弯管接头处产生非常大的喷射反力,这会影响消防车在作业时的安全与稳定性,特别是当高压水流经过炮体的内腔时,因流动环境的变化,使得流体在受到弯曲的内壁面作用时其流动状态发生被迫性改变,对应的固体壁面处则会受到流体对其的持续反作用 [4] ,这种情况的存在极易使得管道内部因强震荡的原因导致焊缝处发生破裂。通过找出不同影响因素与过流时的喷射反力的关系,这对工程师在后续弯管设计时避免了“拍脑袋”现象,因此,这项研究具有一定的工程意义。
近些年,针对喷射反力的研究也非常多。贾传娣等 [5] 在车载消防炮喷射反力的研究过程中提出,同一工况下,喷射反力仿真及实验数据相对误差在6%以内。车载消防炮的喷射反力与流量正相关,得出的拟合公式可以作为消防炮喷射反力与流量关系的简单计算公式。
胡国良等 [6] 采用Fluent流场仿真软件对一种新型固定式消防水炮炮身内部流体流态进行了仿真分析,得到较好的炮身形状及结构;并对消防水炮炮头喷嘴射流性能进行了仿真分析。结果表明:所设计的新型固定式消防水炮能满足实际消防作战使用要求。
何猛等 [7] 对消防炮作业时的受力进行理论分析,通过Fluent仿真研究入口压力分别为0.5、1.0、2.0、3.0、4.0 MPa时后坐力的大小,并将该值导入动力学模型,分析消防炮在不同工况下作业时对整车静态侧翻角的影响。
胡国良等 [8] 针对目前水力自摆式消防水炮后坐力大、容易倾翻的不足,利用Fluent流场软件对水力自摆式消防水炮内部流场进行了仿真,仿真结果表明现有水力自摆式消防水炮内流道截面形状的变化及过渡不平顺,容易使消防水炮出现流速不均匀,造成消防水炮能量损失和后坐力增大。
张俊等 [9] 对几种不同出口直径和锥角的锥形喷嘴水射流反推力进行了理论分析和仿真计算,研究了压力、流量和锥形喷嘴的结构参数对反推力及反推力系数的影响,从而确定锥形喷嘴的最佳结构参数。
胡国良 [10] 在对消防水炮流道优化的研究设计过程中主要研究了进水压力与水炮射程的数量关系,验证优化设计后的性能。
上述文献多为流量或进口压力与喷射反力的关系,而弯管接头出进口面积比、弯角两类结构参数与喷射反力的关系却鲜有文献进行相关研究,因此有必要对不同进出口面积比、弯角、进口水流量与喷射反力的关系进行深入研究。
本文首先采用理论和仿真值进行对比,验证了仿真模型的正确性,随后采用仿真的手段对不同进出口面积比、弯角、进口水流量与喷射反力的关系进行深入研究,得到不同参变量与喷射反力的关系式,这为后续管管的设计提供了一定的理论指导。
2. 理论与仿真对比
2.1. 理论计算
如图1所示为弯管受力分析简图。
本计算中:如图1管道受力分析简图,规定y方向进口面积为A1,流速V1;x方向出口面积为A2,流速V2。设弯管进出口面积比为1 (即A1 = A2),进出口管道直径D1 = D2 = 100 mm,转弯半径R = 60 mm,弯角θ = 90˚,流量Q = 30 L/s。由喷射反力理论计算公式可得 [11] :
Fx = qvρ(V2 − 0) = 114.59 N;
Fy = qvρ(0 + V1) = 114.59 N。
2.2. 仿真计算
2.2.1. 模型
如图2所示为对应的弯管三维模型。
将模型导入流体仿真软件中,采用多面体网格对其进行网格划分,确定网格单元尺寸之前对网格无关性进行了验证,如图3所示。
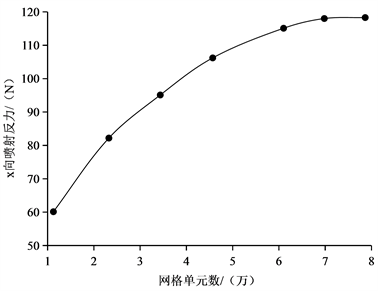
Figure 3. Grid independence verification
图3. 网格无关性验证
由图3发现网格单元数在超过6.5万个后管道出口动压变化很小,因此最后固定好单元尺寸,考虑到计算成本以及计算精度,最后共划分了69,802个网格单元,如图4所示为弯管的网格模型。
模型边界条件设置如下 :1) 入口为质量流量Q = 30 kg/s;2) 出口为压力出口边界,压力为0;3) 其他壁面设为无滑移壁面。假设水为不可压缩流体。主要边界条件具体见图5所示。
本计算在商业计算软件Star CCM+中进行且采用的湍流模型为标准的K-ε模型。
2.2.2. 计算结果
如图6和图7分别表示管道中间截面速度矢量分布与压力分布。
由图6,图7可知:弯角处流体速度流动非常复杂,并且高速区在弯角内侧,该区域还存在较大的负压,影响流体的流动。另外从软件中可以提取出x向和y向的喷射反力:
Fx = 118.032 N, Fy = 130.135 N
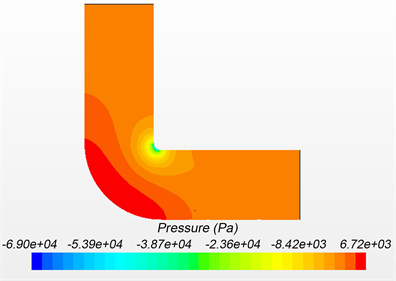
Figure 7. Cloud map of pressure distribution
图7. 压力分布云图
2.2.3. 理论与仿真计算对比
表1给出了水质量流量Q = 30 kg/s、进出口直径相同(D1 = D2,进口面积为A1,出口面积为A2,出进口面积比a = A2/A1 = 1)、弯角θ = 90˚且转弯半径R = 60 mm时对管道壁面反冲压力的理论值和仿真值对比情况。

Table 1. Comparison of theoretical and simulated recoil pressures
表1. 反冲压力的理论值和仿真值对比
由表1可知:理论值和仿真值的一致性较好,误差最大控制在15%以内。误差产生的原因是:1) 理论公式里面没有考虑实际转弯半径,而实际上转弯半径对内部的流动带来非常大的影响,这是主要原因;2) 模型的简化,包括不考虑内壁面摩擦等因素,这是次要原因。实际上,仿真值更接近于真实的情况,后续的分析中均采用仿真值来对不同的参数对喷射反力的影响进行分析。
3. 不同参数下的喷射反力
3.1. 改变弯角
固定参数有:设流量Q = 30 L/s,进出口管道直径D1 = D2 = 100 mm (即出进口面积比a = A2/A1 = 1),转弯半径R = 60 mm。当弯角θ = 30˚~100˚时,通过仿真计算得到不同弯角角度θ与x、y向喷射反力的关系,具体见表2。
如图8所示为x、y向喷射反力与弯角θ的关系图,而且还对两者的关系进行了拟合。
由图8可知:x向喷射反力Fx和y向喷射反力Fy与弯角θ均呈线性关系,只是x向喷射反力Fx与θ呈正线性相关,而y向喷射反力Fy与弯角θ呈负线性相关。具体的关系式如下:
Fx = 0.8675θ + 43.869;
Fy = −2.1421θ + 319.09。

Table 2. The relationship between angle θ and jet reaction
表2. 弯角θ与喷射反力的关系
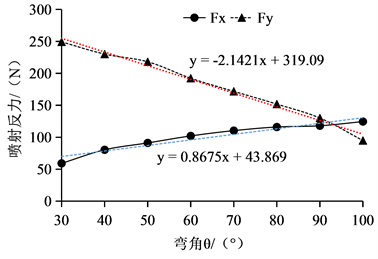
Figure 8. Relation between x and y jet reaction and angle θ
图8. x、y向喷射反力与弯角θ的关系
3.2. 改变流量
固定参数有:设转角θ = 90˚,进出口管道直径D1 = D2 = 100 mm (即出进口面积比a = A2/A1 = 1),转弯半径R = 60 mm。当水质量流量Q = 30~90 L/s,时,通过仿真计算得到不同弯角角度θ与x、y向喷射反力的关系,具体见表3。

Table 3. Relation between mass flow Q and jet reaction
表3. 质量流量Q与喷射反力的关系
如图9所示为x、y向喷射反力与水质量流量Q的关系图,而且还对两者的关系进行了拟合。

Figure 9. Relation between x and y jet reaction and mass flow rate Q
图9. x、y向喷射反力与质量流量Q的关系
由图9可知:x向喷射反力Fx和y向喷射反力Fy与弯角θ之间均具有正线性相关的关系,且x向的喷射反力Fx随着质量流量的增大而增大幅度比y向的喷射反力Fy要打。具体的关系式表述如下:
Fx = 19.016Q − 528.43;
Fy = 25.327Q − 734.12。
3.3. 改变进出口面积比
固定参数有:设水质量流量Q = 30 kg/s,转角θ = 90˚,转弯半径R = 60 mm。当进口直径D1 = 100 mm (进口面积为A1)通过改变出口直径D2 (出口面积为A2),使得进出口面积比a在0.25~1.75之间变化时,通过仿真计算得到不同出进口面积比δ与x、y向喷射反力的关系,具体见表4。

Table 4. The relationship between the area ratio a and the ejection reaction
表4. 出进口面积比a与喷射反力的关系
如图10所示为x、y向喷射反力与出进口面积比a的关系图,而且还对两者的关系进行了拟合。
由图10可知:x向喷射反力Fx和y向喷射反力Fy与弯角θ之间关系较复杂,总体而言以出进口面积比a = 1为界,当a > 1,时,喷射反力随着a的增大基本不变,而当a < 1,时,喷射反力随着a的增大急剧变小;喷射反力与出进口面积比a的关系可以用多项式进行描述,具体表达式如下:
Fx = 352.02a4 − 1726.2a3 + 3148.4a2 − 2597.5a + 941.92;
Fy = −1945.1a5 + 11287a4 − 25463a3 + 28009a2 − 15190a + 3439.9。
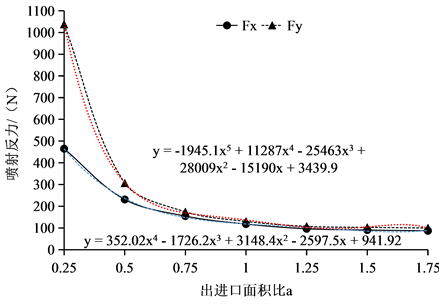
Figure 10. Relation between x and y injection reaction and inlet area ratio a
图10. x、y向喷射反力与出进口面积比a的关系
4. 结论
1) 针对消防车弯管接头影响因素较多且鲜有理论支撑导致其难以设计等难题,通过理论计算对仿真模型进行验证,在两个方向上的喷射反力的理论计算值与仿真值一致性较好,验证了仿真模型的正确性;
2) 采用仿真手段研究了不同弯管转角、不同进口流量、不同出进口面积比与弯管接头过流时在两个方向上的喷射反力的关系。弯管转角与两个方向上的喷射反力均呈线性关系,只是x向喷射反力Fx与θ呈正线性相关,而y向喷射反力Fy与弯角θ呈负线性相关;进口流量与两个方向上的喷射反力均呈正线性关系;出进口面积比与两个方向上的喷射反力的关系较复杂,均呈现出多项式的负相关的关系。
3) 后续的研究中将在理论计算和数值模拟的基础上引入实验研究,进一步验证弯管转角、进口流量、出进口面积比与弯管接头过流时在两个方向上的喷射反力的关系,为类似弯管接头的设计提供理论支撑。
NOTES
*通讯作者。