1. 引言
接触件是电连接器中负责承担信号及能量传输的关键组件,其接触性能的可靠性能够直接决定电连接器的有效寿命。而开槽收口式接触件以其结构简单、信号传输稳定等特点成为最广泛最常用的一类接触件 [1] 。
目前,国内外研究人员们大多着眼于各种外界环境及变化的工作条件对接触性能的影响进行研究。如:Kong等 [2] 对高频连接器进行了微动实验研究电接触的接触性能;Ren等 [3] 对典型的圆形电连接器进行了多应力自动振动测试研究导致连接器接触性能退化失效的主要因素;骆燕燕等 [4] [5] [6] 以某型航空电连接器为研究对象,分别研究了插拔、冲击及振动对电连接器接触性能退化的影响;Kehong等 [7] 讨论并分析了环境温度应力引起的电连接器接触件间歇性故障问题;郑淑梅等 [8] 通过ansys仿真软件对航空电连接器在低温环境下的温度场进行了仿真研究。在众多研究中,未有针对开槽收口量所展开的研究,而收口量作为该类型接触件的关键设计参数之一,若忽视接触件之间的不同收口量对接触性能退化情况产生的差异,将对接触件可靠性评估结果带来误差,因此有必要对贮存状态下开槽收口量对接触件接触性能的影响展开研究。
本文以开槽收口式电连接器接触件为研究对象,针对贮存状态下收口量对接触件的影响及其寿命评估问题,从机理层面出发建立收口量与接触性能之间的数学关系,通过开展加速试验分析收口量对接触件贮存寿命的影响并实现其寿命评估与模型验证,为评估电连接器贮存寿命提供基础数据。
2. 接触件贮存环境下失效机理分析
接触件作为负责电连接器电信号导通的关键组件。在电连接器中的位置如图1所示,通常接触件接触区周围会灌入密封件以保障外界空气、杂质难以进入接触区造成接触件腐蚀、污染等现象,同时两端绝缘件将压紧接触件,保障接触件电气连通的同时与其他部分形成空间上的隔离,进一步提高了电连接器抵御外部侵蚀的能力及接触件的稳定性。
接触件由插针与插孔所组成,而开槽收口式接触件插孔形状为开槽簧片状,其中开槽数将会影响簧片截面形状,通常有开两槽、四槽、六槽等多槽数之分,如图2所示为某型开两槽接触件三维结构图。
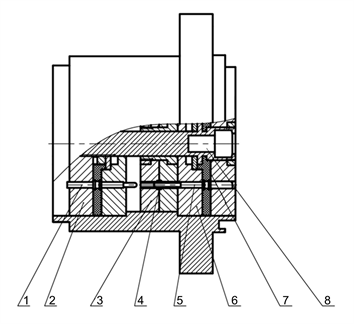 1、4、5-接触件;2、3、6-绝缘件;7-密封件;7-机械连接件
1、4、5-接触件;2、3、6-绝缘件;7-密封件;7-机械连接件
Figure 1. Partial sectional view of a type of electrical connector socket
图1. 某型电连接器插座的局部剖视图
 (a) 插孔
(a) 插孔  (b) 插针
(b) 插针
Figure 2. Three-dimensional structure diagram of the contact
图2. 某型电连接器插座的局部剖视图
接触性能失效作为电连接器的主要失效模式,在贮存期间主要表现为接触电阻随着时间逐渐增大至超过失效阈值 [9] ,从而使电连接器信号传输受到阻碍。在贮存状态下,造成接触电阻增大的原因主要是由于接触表面氧化腐蚀物堆积使膜层增长引起膜层电阻增大所导致,同时温度与收口量均会对接触件氧化产生影响。
2.1. 接触件表面氧化机理
接触件的基体材料大多为铜的合金材料,如最常用的锡青铜、铅黄铜、铍青铜等,而铜作为有色金属其化学性质较为活跃,若将其裸露在空气中,极易与空气中的氧气发生氧化反应形成氧化腐蚀物沉淀在铜表面,进而阻碍了电信号的传导或传输。因此,通常会在铜的表面镀金以形成保护膜,起到化学屏蔽与阻隔作用,但镀金层并非完全致密的,它的晶体表面呈现出凹凸分散不均的状态 [10] 。由于生产方面的实际问题,镀金层往往是非常薄的一层,因此无法避免会存在一些细小的微孔或裂纹,使空气中的O2与H2O进入基体与铜发生氧化还原反应,总化学反应方程式为
,生成的Cu2O堆积在孔隙中,逐渐溢出形成薄膜,进而增大了接触件的膜层电阻。
2.2. 温度对接触件的影响
1) 加速接触面氧化
温度会显著影响氧化膜层的生长速度。这是由于温度的升高会使Cu+的内部活性能增大,加速了Cu+越过镀层向外扩散的速率,进而加快氧化反应。随着Cu2O的膜层厚度不断增加,接触电阻不断增大,最终造成电连接器因接触电阻超过失效阈值而发生接触失效。
2) 接触压力减小
为保证插针与插孔的紧密插合,当光轴插针插入插孔簧片时,插针会撑开插孔簧片使其发生弹性变形,产生一种弹性回复力使簧片与插针之间形成稳定接触压力,接触件插合过程如图3所示。在应力的作用下,插合后的簧片随着时间延长缓慢发生蠕变与应力松弛效应,使金属簧片逐渐从弹性变形转变到塑性变形 [11] ,从而使接触件的接触压力减小。根据有关研究表明,应力松弛现象与环境温度密切相关,升高温度能够加快材料内部原子运动加快应力松弛过程,造成接触力的加速丧失 [12] 。
 (a) 插合前
(a) 插合前 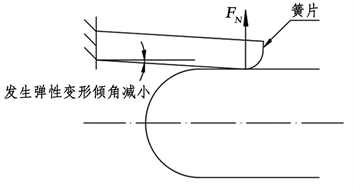 (b)插合后
(b)插合后
Figure 3. Diagram of the process of inserting a pin into a spring
图3. 插针插入簧片过程示意图
3) 镀层剥落
在贮存状态下,温度的波动会引起接触件材料发生微小的相对运动,产生微动磨损或疲劳,同时随着温度的升高,镀金层与基体铜的结合力下降,进而使镀金层发生剥落现象。这种镀层剥落现象会导致基体铜暴露在空气中的面积增大,进而加速其氧化速率,增大接触电阻,降低接触性能。
2.3. 收口量对接触件的影响
对于开槽收口式接触件,开槽收口量是其在生产过程中,以过盈设计生产插孔而后对插孔簧片端部进行收口工序时产生的收口位移量,这样能够使接触件插合后能够形成一定接触压力。即开槽收口量越大,接触件插合后产生的接触压力就越大,收口量示意图如图4所示,图上f表示收口量。

Figure 4. Schematic diagram of reed closing quantity
图4. 簧片收口量示意图
研究表明 [13] ,适当增加外部压力能够有效抑制原离子扩散,进而抑制接触表面氧化速率。这种扩散现象可以理解为在反应过程中,原离子需要克服能量势垒从一个间隙位置跳跃到另一个间隙位置,增加压力能够增大这种能量势垒,使原离子移动时需要耗费更大的能量,进而氧化膜生长速率也就得到了减缓 [14] 。通常计算接触压力时会将簧片近似为悬臂梁,根据悬臂梁力学表达式可得
(1)
式中,F为接触件接触压力;E为插孔簧片的弹性模量;
为插孔簧片中性轴的惯性矩;
为簧片发生弹性变形产生的挠度;L为簧片悬臂部分长度。
接触件简化后的悬臂梁力学模型示意图如图5所示。
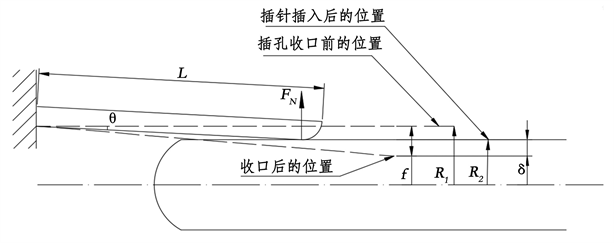
Figure 5. Mechanical model diagram of contact element cantilever beam
图5. 接触件悬臂梁力学模型示意图
如图5所示,
为簧片收口前的半径,
为插针半径,
为插针与插孔之间的接触压力,
为接触件插合过程产生的转角。那么根据尺寸链关系,簧片挠度可表示为
(2)
根据接触压力表达式可以看出,插孔簧片的收口量越大,则接触件接触压力越大,原离子扩散速率越低,生成氧化膜的速率越慢,接触性能退化越慢。因此,可以不同接触压力表示不同收口量,同时接触压力与插拔力成正比关系,且插拔力相比之下更易测量获得,故试验时可以不同插拔力作为区分,最后折算为相对应的收口量。
3. 接触件接触性能退化建模
3.1. 接触件退化轨迹模型
接触电阻r作为考察电连接器接触件接触性能的关键性能指标,根据经典电接触理论,其主要由接触件导体的体电阻
、接触件导电斑点处的收缩电阻
和接触件表面膜层电阻
三部分组成 [15] 。即
(3)
根据失效机理分析可知,接触件接触性能失效主要是由于接触表面氧化膜层堆积使膜层电阻增长所造成,而体电阻与收缩电阻主要由接触件自身材料、结构及生产工艺参数所决定,可视为定值,则可令
表示体电阻与收缩电阻作为接触件出厂后无膜层状态下的接触电阻初值。那么接触电阻可进一步表示为
(4)
对于上述膜层电阻,目前在工程应用方面常采用下式表示 [16]
(5)
式中,
导电斑点上的平均隧道电阻率,与接触件表面氧化膜层厚度有关;
为霍尔姆半径,表示所有导电斑点面积累加后的等效圆半径,与接触压力及导体材料硬度有关。
由隧道效应理论研究可知,可得平均隧道电阻率
与氧化膜层的平均厚度
满足如下关系 [17]
(6)
式中,
、c为待定参数。
根据失效机理可得,接触件表面氧化膜增长主要是由于接触件基体材料的Cu+通过镀层孔隙及缺陷扩散至接触表面发生氧化反应生成Cu2O所导致。根据金属腐蚀学及失效物理基础,假设开始试验时接触件表面无氧化膜层,则氧化膜的生长速率可表示为
(7)
式中,k为氧化反应速率。
由阿伦尼斯方程,氧化物生长速率k与绝对温度T之间的表达式为
(8)
式中,A为常数;
为扩散激活能;
为玻尔兹曼常数。
物体内部原子扩散的有效激活能可被描述为
[18] ,其中J为接触应力,在挤压场中接触应力为负值,拉伸场中接触应力为正值,
为应力J做的功。接触压力F与接触应力的关系如下
(9)
式中,W表示簧片宽度;h表示簧片厚度。
根据霍尔姆的电接触原理,接触压力改变会引起接触件接触面积的变化,接触压力与接触面等效面积
、导电斑点等效半径
之间的数学关系为
(10)
式中,
为小于1的系数,与接触面的压痕比深度有关。
将上述整合后可以进一步得到膜层电阻表达式
(11)
将上式(11)代入式(4)中,即可得到接触件的退化轨迹模型
(12)
3.2. 接触件加速退化方程
为了便于应用,将式(12)进行简化,令
,
,则可以转化为
(13)
其中,α表示膜层电阻退化率与温度之间的关系,
表示模型参数。
对α取对数得
,可见
为较多随机变量的综合,根据中心极限定理,可认为
服从正态分布,则α服从对数正态分布,即
,
和
分别表示退化分布的对数均值和对数标准差。对数均值
可表示为
(14)
其中,
、
为待估计的参数。
3.3. 接触件可靠性模型
若将接触电阻的失效阈值假设为D,那么根据式(14)可以得到接触件的贮存寿命
为
(15)
由于退化率α服从于对数正态分布,那么接触件的可靠性模型可表示为
(16)
式中,
表示标准正态分布函数。
4. 接触件加速试验方案
以开槽收口式接触件为试验对象,接触件基体材料为锡青铜,插针直径为1.5 mm,为避免不同镀层接触件对试验结果产生影响,选取镀金层厚度1.0 μm,插拔力通过测试筛选确定为1.0 N、1.7 N及2.4 N的三组样品进行试验。根据前期研究经验,试验所采取的加速温度应力水平为105℃、125℃、140℃及158℃。为了保证试验精度,在低应力水平105℃下投放样本量为25个,其他温度下投放样本量为20个,试验截尾时间为2500小时,试验测试指标为接触电阻。具体试验方案如下表1所示。

Table 1. Accelerated test schedule
表1. 加速试验方案表
在测试接触电阻时采用开尔文四线法以达到消除导线电阻对试验数据产生影响的目的,开尔文四线法的测试原理图如图6所示。
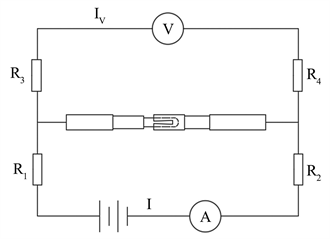
Figure 6. Kelvin four-wire test schematic
图6. 开尔文四线法测试原理图
图中的
、
、
、
分别为四根导线的电阻。在试验时,通过调节稳压源将导通电流设为1 A,根据欧姆定律,电压表上示数即为接触件样品接触电阻值。试验测试平台如下图7所示。

Figure 7. Kelvin four-wire test platform
图7. 开尔文四线法测试平台
5. 试验数据统计分析及模型参数估计
5.1. 不同收口量下的接触件接触性能定性分析
按照试验方案,对各组接触件样品进行定时接触电阻测试,各接触件样品在105℃、125℃、140℃及158℃下分别试验了720 h、648 h、516 h及288 h。各组样品的接触电阻已基本趋于稳定,以140℃为例,接触件接触性能退化轨迹箱线图如图8所示。
图中,“-”表示中位数,“□”表示平均值,“◇”表示异常值。可以看出在环境温度及镀层厚度等影响因素相同的情况下,插拔力越大即收口量越大的接触件,其接触电阻在试验过程中产生的波动越小,接触性能退化速率越慢。
5.2. 加速试验数据统计分析
1) 模型参数粗略估计
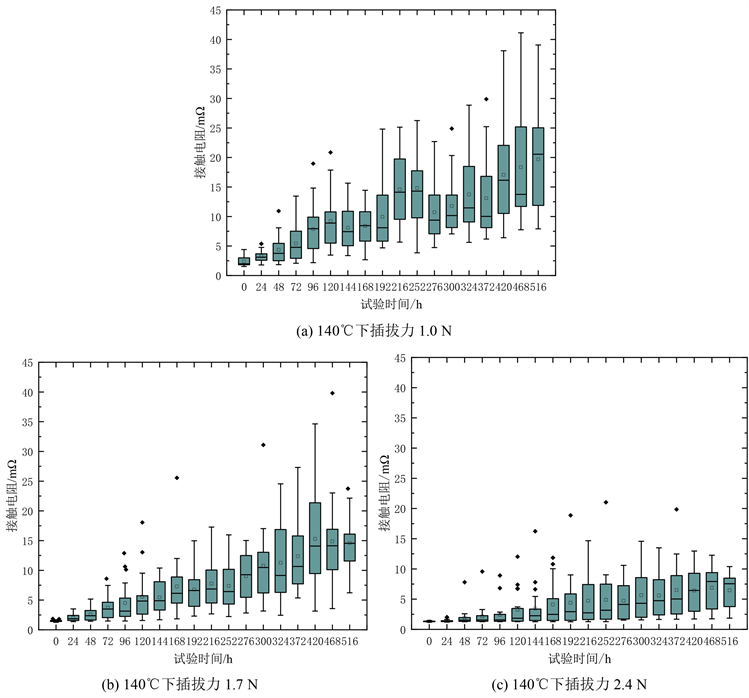
Figure 8. Box diagram of contact performance degradation trajectory of each insertion and withdrawal force group at 140˚C
图8. 140℃下各插拔力组接触性能退化轨迹箱线图
将接触件在t时刻的接触电阻记为
(17)
式中,l表示第l个温度应力水平;j表示第j组接触件;w表示第w个接触件。
通过利用最小二乘估计法,可得各接触件的接触电阻退化率
及模型参数
的粗略估计值,计算表达式如下
(18)
式中,
为实际测量得到的退化数据;
为理论退化轨迹;
为各温度应力水平下各组的测试次数。
各温度应力水平下不同插拔力接触件的接触电阻退化率的
、
及
可以通过下式计算
(19)
(20)
(21)
式中,
为各温度水平下的试验组数。
同理,对式(14)进行参数粗略估计,即可得到第j组接触件的
、
粗略估计值。将上述计算获得的参数粗略估计值作为初始值用于极大似然估计。
2) 模型参数极大似然估计
由于在接触电阻测试时,各种随机因素可能会使测试实际值
与理论值
之间存在一定误差,误差关系可表达为
(22)
式中,
表示测试时所产生的误差,一般可认为其服从标准正态分布,即
。
假设不同组接触件间接触电阻相互独立,根据测试误差及退化率的分布特性,建立似然函数可得
(23)
式中,M为试验温度水平数。
根据似然函数及最小二乘法求解所得粗略参数值,即可求解退化模型中参数
、
、
及
的估计值,结果如表2所示。

Table 2. Degradation model parameter estimates
表2. 退化模型参数估计值
6. 接触件退化模型验证及寿命评估
6.1. 退化轨迹模型检验
根据式(22)可知,该式为接触性能退化轨迹模型的非线性回归模型,采用残差分析法对模型的拟合优度进行检验,通过计算回归平方和SSR与总平方和SST的比值来衡量模型对试验数据的拟合程度。即
(24)
式中,
,
,
为模型估计的拟合数据,
为实测获得的数据平均值,
为测试得到的测试数据。
根据加速试验数据,求得不同温度组别下各插拔力组的
值如表3所示。

Table 3. R 2 value of inserting and pulling force of each group under different temperature groups
表3. 不同温度组别下各组插拔力的
值
从表中可以看出,各温度水平下各组插拔力的
值均接近于1,因此,认为该回归模型对试验数据的拟合程度较好,即推导的退化轨迹模型正确。
6.2. 退化率分布检验
采用Anderson-Darling检验法对接触电阻退化率是否服从对数正态分布进行检验,根据试验数据及结果,对各温度应力水平下各组插拔力的退化率分布检验P值如表4中所示。

Table 4. P values of insertion and withdrawal forces of each group in each temperature group
表4. 各温度组别下各组插拔力的P值
从表中可以看出,各温度应力水平下各组插拔力的退化率分布检验P值均大于0.05,认为接触电阻退化率服从对数正态分布,即推导的分布类型正确。
6.3. 加速退化方程检验
对加速退化方程的检验即检验接触电阻退化率的对数均值
与温度应力
之间是否存在明显的线性关系。根据式(14)建立线性回归方程
(25)
式中,
为满足Guess-Markov假设的随机误差。
利用4.2节的统计分析方法对接触电阻退化率的对数均值进行估计,再以估计值
对式(25)进行最小二乘估计,得到线性回归方程的估计值
和
。采用方差分析法检验
是否为0,即
(26)
式中,
,
,M为温度应力水平,
。
取显著性水平为0.05,通过查F分布表确定分位数为
,计算各组插拔力的F检验统计量,结果如表5所示。

Table 5. F value of inserting and pulling force of each group in each temperature group
表5. 各温度组别下各组插拔力的F值
从表中可以看出,各组插拔力的检验统计量F均大于18.5,认为接触电阻退化率的对数均值与温度应力水平之间存在显著线性关系,即加速退化方程正确。
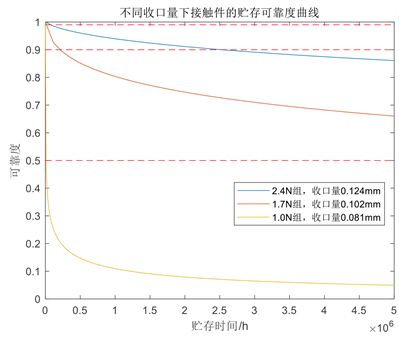
Figure 9. Storage reliability curve under different closure quantity
图9. 不同收口量下的贮存可靠度曲线
6.4. 可靠性评估
在验证了模型及机理的正确性后,根据插拔力与接触压力的关系式
,其中μ表示接触件摩擦系数,n表示簧片数量。将各组插拔力数值代入式(1)中,可得插拔力1.0 N/1.7 N/2.4 N分别对应收口量0.081 mm/0.102 mm/0.124 mm。再根据表2中的参数估计值,将其代入式(16)中,即可得到各组插拔力在贮存环境(25℃)下的可靠度函数,不同插拔力可靠度曲线如图9所示。
由图9可见,收口量越大的接触件在相同贮存时间的条件下其可靠度越高,贮存寿命越长。
7. 总结
本文从失效机理角度分析确定了接触件接触性能失效主要原因是由接触表面发生氧化反应使氧化物堆积所导致,而温度升高会加速接触性能的退化速率,且开槽收口量越大的接触件接触压力越大,对原离子扩散现象的抑制效果越强,性能退化越慢;建立了接触件的性能退化模型,通过开展加速试验证明了开槽收口量越大的接触件,其接触电阻在试验过程中产生的波动越小,相同贮存条件下的可靠度越高,并利用试验数据对模型进行了验证,证明了所建模型的正确性。
基金项目
浙江省重点研发项目(2021C01133)。