1. 引言
针对普通混凝土材料脆性大、耐久性差等问题,近些年来许多学者为研制出能提升混凝土性能的新型材料做了大量研究。Li等 [1] 成功研制出一种高延性纤维增强水泥基复合材料(ECC),以水泥、砂、矿物掺合料等构成基体,2%体积掺量的乱向分布短纤维为增韧材料,其具备高韧性、高延性、优秀的抗拉性能和优异的裂缝控制能力。相对聚乙烯(PE)纤维来说,聚乙烯醇(PVA)纤维成本较低,与水泥基体化学粘结力较强。除此之外,PVA的抗渗性 [2] 、抗冻性 [3] 和抗碳化 [4] 等性能都远高于普通混凝土,是目前ECC试验研究和实际工程应用最为广泛的增韧材料 [5]。
传统ECC中的胶凝材料以造价高昂的水泥为主,在凝结硬化过程中的干燥收缩较大 [6]。水泥生产过程排放大量二氧化碳会造成环境污染,因此国内外学者开始研究使用工业固废来代替水泥。荣传新等 [7] 研究表明,将普通脱硫石膏经高温煅烧后生成β型半水石膏,再将其与矿物、化学激发剂混合搅拌则形成改性脱硫石膏,以改性脱硫石膏替代水泥可以增强混凝土抗压强度和抗折强度;Ji等 [8] 用粉煤灰部分替代水泥,发现替代率在30%~40%之间时,对抗压和抗折强度的提升效果最好,通过实验发现,PVA纤维和ECC基体的界面得到有效改善,实现了ECC材料的拉伸应变–硬化特性 [9] ;Yu等 [10] 用硅灰代替水泥,可以密实填充基体,从而起到减小孔隙率的作用,解决粉煤灰代替水泥后基体早期抗折强度低的问题,从而提高ECC基体强度。与此同时,石英砂资源有限,价格昂贵,以河砂代替传统ECC常用的石英砂,能明显降低成本 [11]。
结合国内外研究成果,本文采用改性脱硫石膏、粉煤灰和硅灰组成ECC的胶凝材料体系,P·O 42.5级水泥配置高强混凝土,用河砂来替代石英砂,以此来提高传统ECC的力学性能,实现工业废渣类材料再利用。本文所研制的ECC预计用于煤矿井壁修复 [12],鉴于矿井缝隙较小,不同井壁混凝土强度要求不同,所以对ECC坍落度以及强度有一定要求。本文结合现有ECC研究成果,开展一系列力学性能试验,研制出适应于煤矿井壁修复的高强高韧性混凝土配合比,以期提供ECC在井壁修复领域的应用基础,为我国煤矿井壁修复提供重要帮助,为实现我国“绿色可持续煤矿”贡献一份力量。
2. 实验材料及方法
2.1. 原材料
试验中水泥采用安徽海螺公司生产的P·O 42.5级普通硅酸盐水泥;硅灰购于山东博肯硅材料有限公司;淮南平圩电厂生产的Ⅰ级粉煤灰;上海每天节能环保科技公司生产的粒径约为40 μm的改性脱硫石膏;细骨料采用最大粒径为0.5 mm的细河砂;减水率为25%~30%的聚羧酸高性能减水剂购于江苏苏博特公司;纤维采用日本可乐丽12 mm PVA纤维,纤维性能参数如表1所示;采用山西杰克科技有限公司生产的KC-2混凝土膨胀剂;拌和用水为实验室自来水。

Table 1. Performance parameters of PVA fiber
表1. PVA纤维性能参数
2.2. 试验设计
为研究胶凝材料和外加剂对ECC力学性能的影响,本试验选取的研究因素为硅灰掺量、改性脱硫石膏掺量、膨胀剂掺量和减水剂掺量,每个因素选取三个水平,制作四因素三水平L9 (34)正交表 [13] (见表2)。试验指标为ECC坍落度、28 d抗压强度、28 d抗拉强度、28 d抗折强度。根据李晓琴等 [14] 的实验研究,本次试验的水胶比取0.25,砂胶比取0.35,纤维体积比取0.2。

Table 2. Orthogonal table of four factors and three levels
表2. 四因素三水平正交表
2.3. 试件制备和试验方法
2.3.1. 试件制备
具体步骤如下:首先将称好的胶凝材料和河砂加入JJ-5水泥砂浆搅拌机中干拌2 min,然后将搅拌好的水和减水剂混合液倒入搅拌机中湿拌3 min。将手工分散好的纤维均匀撒入拌和物中搅拌10 min,以保证纤维能够在水泥基体中均匀分散。为使试件充分密实,分两次浇筑,每次在振动台上振捣20 s左右,抹平浇筑面。浇筑24 h后,拆除模具,将试件放入温度为(20 ± 2)℃、湿度为95%的恒温恒湿养护箱中,养护到试验所需的龄期 [15]。
2.3.2. 试验方法
按照GB/T 50081-2002《普通混凝土力学性能试验方法标准》中的相关规定 [16] 开展物理力学性能试验。使用时代试金WAW-1000电液伺服万能试验机以2.5 mm/min的加载速率对100 mm × 100 mm × 100 mm的立方体试件进行抗压强度试验;在0.2 mm/min的加载速率下对400 mm × 70 mm × 16 mm的试件进行抗拉强度试验,为了保证试件轴心受拉,在试件两端粘贴碳纤维布和1 mm厚的铝板加固;对40 mm × 40 mm × 160 mm的试件以0.5 mm/min的加载速率进行抗折强度试验;坍落度试验测试方法,以坍落高度作为不同配合比ECC的流动性指标。每组配合比的每种尺寸制作三个试件,试验结果取三个试件的算术平均值。
3. 试验结果与分析
3.1. 试验现象
通过图1(a)、图1(b)对比观察出ECC立方体试件分别在7 d和28 d受压的破坏形态。ECC的受压破坏过程与普通混凝土有明显区别,破坏过程中纤维断裂声清晰,试件在压缩下仍能保持其完整性,表现出优良的延性。PVA纤维的掺入控制了裂纹的扩展,ECC的抗压强度和韧性得到提高。
由图1(c)可以看出,ECC试件在直接拉伸试验下的破坏形态,基体在达到初裂应变时,开始出现裂纹。随着碳纤维编织网与基体之间的滑移,裂纹开始传播,在达到峰值应力后,演变成一条纹路较宽的裂纹,这个过程表现出明显的多缝开裂特性。
通过图1(d)分析ECC试件在四点弯曲试验中的破坏过程,ECC试件在弯曲载荷作用下开裂,由于纤维的桥联作用,导致应力不断重新分布,同时伴随着新裂缝产生。直到试件达到极限应力时,纤维桥联作用开始失效,不再出现新的裂缝。现有裂缝开始缓慢扩展,其中第一条产生的裂缝宽度和深度迅速扩展,试件最终发生破坏。ECC在整个过程中表现出优秀的应变硬化和多缝开裂特性。

Figure 1. Failure forms of specimens under various mechanical properties tests
图1. 试件在各种力学性能测试下的破坏形态
3.2. 试验结果极差分析
为研究实验因素(硅灰、改性脱硫石膏、膨胀剂和减水剂掺量)对试验指标(ECC坍落度、立方体抗压强度、抗折强度和抗拉强度)的影响,借助SPSS数据分析软件,对表3试验数据进行极差分析,极差分析结果如表4所示。Kij表示因素j所在列在对应i水平下的试验数据之和,i = 1, 2, 3;j = A, B, C, D。表中Kij、kij、Rj之间的关系为:

Table 3. Test results of ECC slump and strength
表3. ECC坍落度和强度试验结果

Table 4. Range analysis results of ECC slump and strength
表4. ECC坍落度和强度的极差分析结果
试验指标受到实验因素的影响程度可以用Rj来反映。为了更加直观地显示各因素水平的变化对试验指标的作用,以各因素的水平变化为横坐标,以上述极差分析得到的各试验指标在不同水平下平均值为纵坐标,绘制水平与指标的曲线图,发现了如下规律:
由表4可知,各因素对ECC坍落度的影响程度为:减水剂掺量 > 硅灰掺量 > 改性脱硫石膏掺量 > 膨胀剂掺量;最佳组合为A1B1C2D3。由图2(a)可以看出,减水剂和硅灰掺量影响坍落度较显著,其中减水剂掺量从1.3%增加到1.9%,坍落度提高了41.6%,硅灰掺量从10%增加到30%,坍落度降低了28.4%;脱硫石膏掺量越大,坍落度越小;膨胀剂掺量对坍落度的影响呈波动状,极差为8.67 mm最小。
通过对表4的分析可以发现,各因素对ECC抗压强度的影响程度为:硅灰掺量 > 减水剂掺量 > 膨胀剂掺量 > 改性脱硫石膏掺量;最佳组合为A3B2C1D3。由图2(b)可知,硅灰掺量和减水剂掺量与抗压强度成正比,抗压强度最大可以达到66.51 MPa;膨胀剂掺量与抗压强度成反比,抗压强度最小为62.56 MPa;当脱硫石膏掺量超过6%以后,抗压强度开始降低。
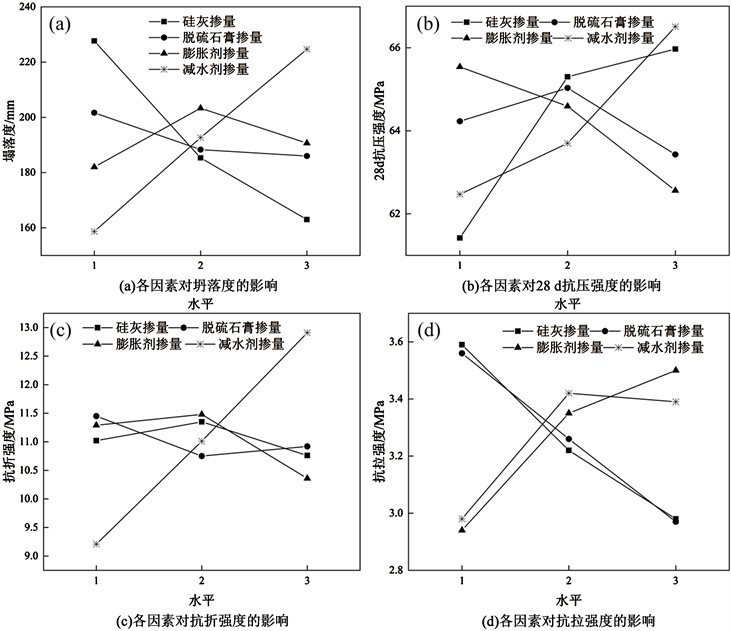
Figure 2. Influence of various factors on collapse, 28-day compressive strength, flexural strength and tensile strength
图2. 各因素对塌落度、28 d抗压强度、抗折强度、抗拉强度的影响
由表4可看出,各因素对ECC抗折强度的影响程度为:减水剂掺量 > 膨胀剂掺量 > 改性脱硫石膏掺量 > 硅灰掺量;最佳组合为A2B1C2D3。由图2(c)可知,减水剂掺量和抗折强度呈正相关,减水剂掺量为1.9%的三组抗折强度均达到12 MPa以上,最大为14.06 MPa;当膨胀剂和脱硫石膏掺量超过6%以后,抗折强度出现两种不同的变化趋势,膨胀剂使其强度减小,脱硫石膏使其强度增大;硅灰掺量对抗折强度影响最小,极差为0.58 MPa。
将表4得到的极差结果归纳发现,各因素对ECC抗拉强度的影响程度为:硅灰掺量 > 改性脱硫石膏掺量 > 膨胀剂掺量 > 减水剂掺量;最佳组合为A1B1C3D2。由图2(d)可以看出,硅灰和脱硫石膏掺量对抗拉强度的影响呈负相关,硅灰和脱硫石膏掺量从1水平增加到3水平,抗拉强度均降低了17%;膨胀剂掺量从4%增加到8%,抗拉强度升高了19%;减水剂掺量对抗拉强度的影响甚微。
4. 试验结果的线性回归分析
利用统计软件SPSS对试验得到的数据进行多元线性回归分析,假设因变量与多个自变量之间的线性关系模型为:
其中,y为因变量(y1为坍落度;y2为28 d抗压强度;y3为抗折强度;y4为抗拉强度);x为自变量(x1为硅灰掺量;x2为改性脱硫石膏掺量;x3为膨胀剂掺量;x4为减水剂掺量);βi (i = 0, 1, 2, 3, 4)为回归系数;ε为随机误差项。根据SPSS的计算结果,得到各因变量的方差分析表(表5~表8)和关于β的最小二乘估计。

Table 5. Variance analysis of Slump variance
表5. 坍落度方差分析
注:β = [197.667, −32.333, −7.833, 4.333, 33.000], y1 = 197.667 − 32.333x1 − 7.833x2 + 4.333x3 + 33x4。

Table 6. Variance analysis of compressive strength at 28 d
表6. 28 d抗压强度方差分析
注:β = [59.423, 2.273, −0.402, −1.488, 2.020], y2 = 59.423 + 2.273x1 − 0.402x2 − 1.488x3 + 2.02x4。

Table 7. Variance analysis of flexural strength
表7. 抗折强度方差分析
注:β = [9.056, −0.127, −0.265, −0.463, 1.848], y3 = 9.056 − 0.127x1 − 0.265x2 − 0.463x3 + 1.848x4。

Table 8. Variance analysis of tensile strength
表8. 抗拉强度方差分析
注:β = [3.492, −0.305, −0.295, 0.278, 0.207],y4 = 3.492 − 0.305x1 − 0.295x2 + 0.278x3 + 0.207x4。
对多元回归方程进行显著性检验,通过F检验方法来检测回归方程的整体显著性。坍落度、28 d抗压强度、抗折强度、抗拉强度对应的显著性值依次分别为:0.010、0.043、0.014、0.018,均小于0.05,说明对自变量x整体的线性回归效果显著。通过对每个回归系数进行显著性检验,得到每个因变量的显著影响因素:坍落度的显著因子是减水剂和硅灰;抗压强度的显著因子是硅灰和减水剂;抗折强度的显著因子是减水剂;抗拉强度的显著因子是硅灰、脱硫石膏和膨胀剂。结合以上极差分析得到最优组为A2B1C2D3。
将效果不显著的影响因子删除,以优化模型,重新建立更为简单的回归方程,得到各因变量新的回归方程如下:坍落度y1 = 190.667 − 32.333x1 + 33x4;抗压强度y2 = 55.643 + 2.273x1 + 2.02x4;抗折强度y3 = 7.346 + 1.848x4;抗拉强度y4 = 3.906 − 0.305x1 − 0.295x2 + 0.278x3。
图3为ECC各物理、力学性能的预测值与实测值对比图,由图3可以看出,大部分实测值大于预测值,说明建立的模型拟合效果较好,预测结果比较合理可靠,可以为工程假设提供一定的参考价值。并且可得出各因素预测值与实测值的比值平均数分别为1.0008、1.00002、1.00003、0.99997;比值方差分别为:0.0049、0.0007、0.0034、0.0044。
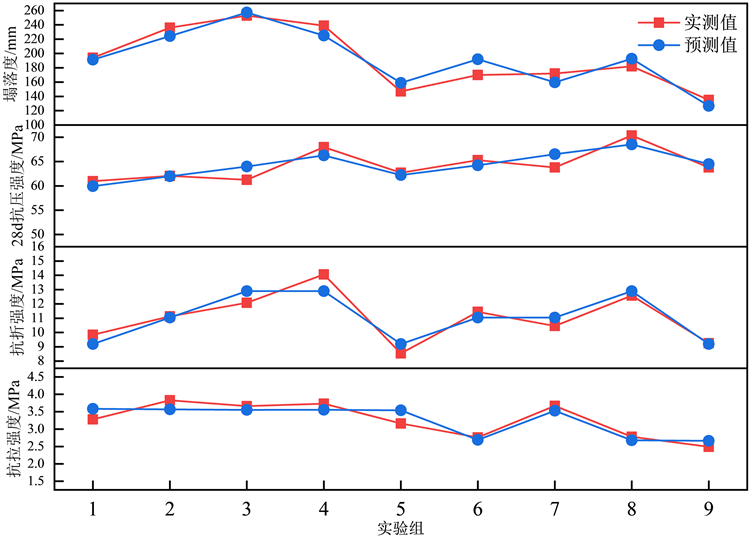
Figure 3. Comparison of the predicted value and measured value of ECC strength
图3. ECC强度预测值与实测值对比
5. 结论
1) ECC的坍落度随减水剂掺量的增大而显著增大,硅灰和改性脱硫石膏掺量会导致坍落度降低;抗压强度随硅灰和减水剂掺量的增大而增大,但膨胀剂掺量则会降低抗压强度;抗折强度随减水剂掺量增加而显著增大,膨胀剂、改性脱硫石膏掺量对抗折强度无明显影响;抗拉强度随硅灰和改性脱硫石膏掺量的增加而降低,膨胀剂和减水剂掺量则相反。
2) ECC坍落度的显著性因素是减水剂和硅灰;ECC抗压强度的显著性因素是硅灰和减水剂;ECC抗折强度的显著性因素是减水剂;ECC抗拉强度的显著性因素是硅灰、脱硫石膏和膨胀剂。综合考虑的最佳组合为:硅灰掺量20%,脱硫石膏掺量4%,膨胀剂掺量6%,减水剂掺量1.9%。
3) 通过对试验结果的多元线性回归分析,得到可以预测ECC配合比试验结果且整体显著的物理、力学性能回归方程,并根据试验结果建立了精度满足工程需求的预测模型,有一定的实际工程参考意义。
NOTES
*通讯作者。