1. 引言
随着互联网技术的发展,网络拓扑日益复杂,业务流量也不断增大,网络拥塞的出现也更加频繁,使得业务流量出现卡顿、丢包等现象,造成服务质量(Quality of Service, QoS)下降,导致用户体验不佳。因此,提出行之有效的网络负载均衡算法来解决网络拥塞问题是十分必要的。
针对网络负载均衡这一问题,主流的算法可以大致分为基于策略的启发式算法和基于模型的优化算法两类。一般而言,启发式类算法是基于拥塞产生的原因提出避免策略而产生的,在特定场景下具有良好效果,例如网络拓扑为多根树的网络数据中心 [1] 等,但是难以适应广域网的复杂拓扑,同时这类算法的效果也没有理论保障。优化模型算法通过将网络建立成数学模型,算法效果一般具有一定理论保证,但根据模型的不同导致精确度和求解难度差异较大。
本文基于SDN (Software-Defined Network)网络的性质,建立了网络负载均衡的数学模型。由于在实际应用中,网络使用者通常是向网络服务提供商(Internet Service Provider, ISP)购买网络使用权,这种场景下网络拓扑是固定的,使用者根据使用的网络链路向ISP付费。因此,本文提出的网络负载均衡模型同时以新增链路数为极小化目标,使其具有更大的应用价值。
2. 背景
作为一种基础设施建设提供者,网络供应商通常从如中国电信、中国移动、AT&T等多家ISP购买网络带宽的使用权,整合后以基础设施即服务(Infrastructure as a Service, IaaS)的形式为客户提供服务。当用户业务规模增加,网络负载上升时,网络供应商通常使用网络负载均衡技术使得网络流量分布均衡,在充分利用带宽资源的前提下提高网络性能和可靠性。网络负载均衡技术可以将网络流量分散到多条链路上,从而充分利用链路资源并降低单条链路的负载,提高整个网络的性能和吞吐量。同时,当网络出现故障或瓶颈时,负载均衡技术可以将流量转移到其他链路上,以保持网络的可靠性和稳定性。
国内外许多专家学者都对网络负载均衡问题进行了深入研究,并针对不同场景下的需求开发了多种网络负载算法。在SDN网络技术 [2] 出现之前,已经有学者认识到了基于最短路的路由算法如RIP、OSPF协议会出现链路热点,造成网络拥塞问题,并提出了如等价多径路由(Equal Cost Multi-Path, ECMP) [3] 等路由策略缓解该问题。在SDN网络出现之后,除一般的转发和路由信息之外,网络的控制平面还可以获得关于包括边缘节点负载信息在内的网络全局信息,大大提升了网络负载均衡算法运行时可以利用的信息量,因此基于这些信息有很多学者为不同的应用场景提出了许多基于全局优化的网络负载均衡模型。
2.1. 基于策略的启发式算法
基于网络拥塞出现的原因,学者首先提出了ECMP负载均衡策略,该策略的思路是将源点汇点相同的不同业务平均分配到多条代价相等的路径上,以避免不同业务在相同链路上出现冲突。该算法可以将流量均衡地分配到多个路径上,避免某些路径因为流量过大而导致拥塞,提高网络吞吐量和负载能力,并且简单、易于实现,目前常见的OSPF-ECMP [4] 等协议都是基于ECMP策略实现的。但是,ECMP要求所有的路径成本相同,如果实际场景中不存在这样的路径就会导致该策略无法有效进行负载均衡,并且由于路由选择算法的不确定性和网络拓扑的复杂性,可能会导致某些路径的负载过高或过低,无法完全实现负载均衡。基于数据中心网络拓扑通常为多根树的拓扑特性,在SDN技术的支持下有学者提出了Hedera负载均衡算法 [1] ,该算法综合考虑网络拓扑、链路成本、流量负载等因素,利用中心控制平面来动态地调整负载均衡策略,以实现高效的流量负载均衡能力。但是由于Hedera采取了为大流单独分配路径的策略,当网络中存在大量的高带宽、大流量的数据流时,Hedera可能无法在进行有效的负载均衡,这可能会导致某些链路负载过高,影响网络性能。另一方面,当网络中存在大量的小流时,由于Hedera采用的是TCP连接级别而不是业务级别的负载均衡策略,这些小流很可能会被映射到同一个服务器上,导致该服务器的负载过高,影响网络性能。从广域网应用的角度看,Hedera算法主要针对数据中心内部的流量负载均衡,难以应用于跨数据中心的网络负载均衡问题中。
2.2. 基于模型的优化算法
基于SDN网络控制平面中央控制器收集到的网络流量信息,可以将网络负载均衡问题建立为数学优化模型,一般目标函数为最小化链路的最大负载,约束条件包括业务约束和链路负载等约束。由于建立了数学优化模型,一般可以得到最优的负载均衡方案,相比其他算法可以得到更精确的负载均衡结果,并且可以根据实际情况调整目标函数和约束条件,适应不同的网络环境和业务需求。在不可分割流的场景下,有学者基于整数规划理论提出了混合整数线性规划模型 [5] ,在可分割流的场景下,还有学者提出了基于多商品流的网络负载均衡模型 [6] 。一般而言,这些模型通常是NP-难的,计算复杂度较高,需要较强的计算能力和时间成本,因此为模型设计高效的求解算法是很有必要的。
本文提出的新网络负载均衡算法也是基于模型的优化算法,但优化目标没有采用最小化链路的最大负载,这是因为在实际应用中由于业务流量波动 [7] ,只需要将最大负载控制在给定的阈值之内即可,而极小化波动的负载计算量较大但收益很小。并且根据IaaS供应商的业务场景特点,我们将极小化目标设置为了新增链路数,这样可以在在阈值内有效利用已有带宽资源,节省成本。同时,我们使用线性规划的方法来求解模型,使用内点法可以保证多项式的时间复杂度,进一步降低了计算成本。
3. 一种新增链路数最小的网络负载均衡算法
3.1. 算法提出
在实际应用中,广域网网络的物理层通常是由ISP建设并负责维护的,之后由ISP按链路带宽出租给IaaS供应商为上层业务提供服务。因此对于IaaS供应商而言充分利用已有带宽资源可以有效节省带宽成本。另一方面,广域网业务复杂、规模庞大,网络负载均衡算法的运行效率的提升可以有效减少计算成本。
因此,我们提出了以新增链路数为极小化目标的优化模型,同时将链路最大负载控制在给定的阈值
内,这样可以有效降低成本并控制网络拥塞。同时,我们采用线性规划方法近似求解该模型,当采用内点法时,该算法具有多项式时间复杂度,可以有效处理广域网中的网络负载均衡问题。
3.2. 模型建立
3.2.1. 符号说明
在网络拓扑
中,其中为V顶点集,E为边集,每条边都具有带宽属性
。网络上承载的业务构成的集合记为业务集D,并且每个业务都具有起点
和终点
,以及所需业务流量
。为了方便讨论,不妨记集合
为业务m当前所使用的边的集合。决策变量为
表示业务m在边e上的流量。
3.2.2. 优化目标
我们的优化目标为极小化新增链路数。对于业务m而言,
可以表示业务是否使用边e,因此
可以对业务m的新增链路进行求和,得到
为其新增链路数,其中
表示从边集E中去掉负载均衡算法运行前业务m使用的边集
后得到的集合。之后再对所有业务进行求和,可以得到所有业务的新增链路数
作为其极小化目标。
3.2.3. 问题约束
该优化问题需要满足的约束条件是业务约束、拥塞约束和非负约束。业务约束要求最优解满足业务m的三个属性,即源点
,汇点
和流量带宽
。我们将该约束化为流平衡约束,即对于图G中每个节点i而言,如果节点i是业务m的源点,那么其流量应净流出
;如果节点i是业务m汇点,那么其流量应净流入
;如果既不是源点也不是汇点,即中间节点或无关节点,其净流量都为零。拥塞约束要求网络中最大负载小于阈值
,因此我们可以对边e上所有业务的流量都求和,并要求利用率小于阈值
,
即
,为了使约束方便线性化求解,我们可以等价的要求每条边都满足该约束,即
。非负约束要求我们的决策变量都是非负的,这是由于问题特性决定的,即
。
3.2.4. 数学模型
基于上述的分析我们可以建立如下的优化模型:
该优化模型的目标是极小化新增链路数,第一个约束是业务约束,要求满足业务需求;第二个约束是拥塞约束,要求最大链路负载不超过给定的阈值
;第三个约束是非负约束,要求所有流量非负。
3.3. 模型求解
由于该模型中使用了零范数刻画链路新增数量,造成目标函数高度非线性,难以直接求解。因此我们考虑使用
范数近似零范数 [8] 。
范数通常比零范数更容易优化,因为它是凸函数,而零范数高度非凸,难以优化。因此在实践中,我们通常使用
范数来近似零范数。由于在我们的模型中决策变量是非负的,近似后的绝对值也可以省去,这样可以得到以下线性规划模型:
该模型是一个标准的线性规划模型,可以使用常用的线性规划求解器求解。通过内点法求解,该模型具有多项式的时间复杂度 [9] 。
4. 数值实验
在数值实验中,我们在Windows 10操作系统中使用Python 3.10编写数值实验程序,线性规划求解器我们选用了HiGHS求解器 [10] 。在实验中,初始流量是使用传统路由算法生成的,之后,我们对比了传统算法和新算法的负载均衡效果。实验表明,传统基于最短路的路由算法确实会导致网络拥塞问题,对比试验结果可以看出我们的算法可以有效将网络负载控制在阈值之内,在新增链路数最小的情况下有效降低了网络拥塞。
4.1. 测试网络拓扑
我们分别在经典拓扑广域网全连接图和随机生成的网络拓扑中对比测试了经典OSPF-ECMP算法与我们算法的效果。网络带宽和业务需求是按照文献 [11] 的方法随机生成的,随机拓扑是按照文献 [12] 的方法随机生成的。拥塞阈值根据文献设置为
,在这个阈值水平下,可以较好地平衡网络性能与网络吞吐量。
4.2. 数值结果
图1是在经典拓扑上的实验结果,我们选取了10个全连接的广域网节点并部署了50个业务。图1左图为网络拓扑示意图,右图横轴为从零开始的链路编号,纵轴为链路负载率,红色水平线表示拥塞阈值
。从图中可以看出虽然网络链路还有冗余,即许多负载远低于阈值的链路,但已经出现了拥塞。通过对比OSPF-ECMP算法结果和我们的算法结果可以看出,OSPF-ECMP算法并不能有效去除网络拥塞,最大链路利用率仍超过了拥塞阈值
,甚至超过了1。这是因为虽然全连接网络拓扑中具有数量庞大的网络链路,但最短路类算法倾向于选择的大带宽、低延时链路并不多,因此往往在这些链路上形成热点,造成网络拥塞。这类算法没有充分利用网络中的链路资源。而我们的算法通过全局优化模型,利用了闲置带宽资源,从图中可以看出,我们的算法提升了OSPF-ECMP算法中闲置部分的利用率,同时将带宽使用率限制在了拥塞阈值
之内,避免了网络拥塞问题。图2是在随机拓扑上的实验结果,与经典拓扑相比,该拓扑增多了网络节点但减少了链路数量,使得问题更难求解,从实验结果来看,该拓扑冗余链路较少,OSPF-ECMP算法和我们的算法都更多的利用了冗余链路,但对比算法并没有有效解决拥塞问题,而我们的算法成功将拥塞控制在了拥塞阈值
之内,因此仍然是我们的算法更具优势。
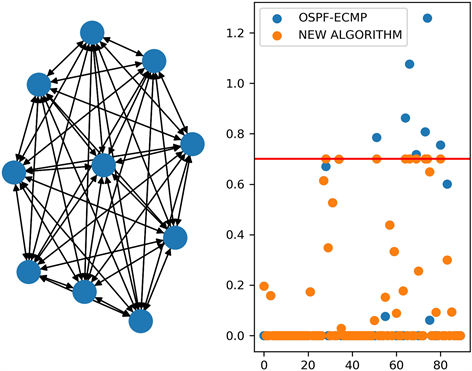
Figure 1. Comparison of OSPF-ECMP algorithm and the new algorithm in classic topology
图1. 经典拓扑中OSPF-ECMP算法与新算法的对比
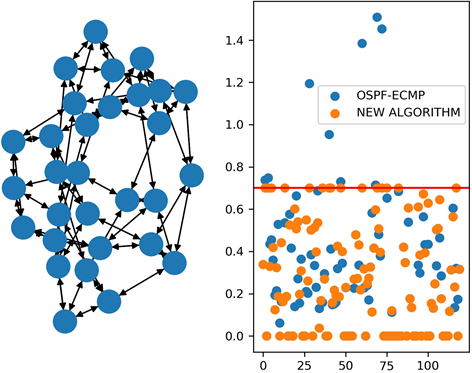
Figure 2. Comparison of OSPF-ECMP algorithm and the new algorithm in random topology
图2. 随机拓扑中OSPF-ECMP算法与新算法的对比
5. 结论
本文提出了一种新增链路数最少的网络负载均衡模型,在实际应用中,该模型可以在避免网络拥塞的前提下节省大量链路带宽成本。该模型为全局优化模型,与启发是算法相比效果具有理论保证,同时该模型可以使用线性规划方法求解,与传统NP-难模型相比具有时间复杂度优势。数值实验表明,我们的算法优于传统的OSPF-ECMP算法,可以有效求解网络负载均衡问题。