基于抛物线OWA熵权–灰关联的配电网规划方案综合决策

Comprehensive Decision-Making of Distribution Network Planning Based on En-tropy Weight and Grey Correlation Optimized by Parabolic OWA

摘要: 为了解决配电网规划方案综合决策中由于定性指标模糊导致的决策主观性强的问题，提出了抛物线OWA熵权和灰色关联度相结合的配电网规划方案综合决策体系。该方法首先通过抛物线OWA将德尔菲法的专家重要度量值进行优化处理，可根据专家量值区分度之间大小自适应改变专家重要度大小，然后通过熵权法对整体指标赋权，按照给定的最优分辨系数 求取熵权灰色关联度，最后对其排序得到最优方案。文中给出了一套配电网规划方案指标体系，并通过实例将该方法与以往多种方法进行对比，验证了该决策方法运算简单，具备良好的主客观融合等特点，具有一定实际意义。

Abstract: In order to solve the problem of strong subjectivity of decision making caused by fuzzy qualitative index in the comprehensive decision of distribution network planning scheme, a comprehensive decision system of distribution network planning scheme based on entropy weight and grey correlation optimized by parabolic OWA was presented. Firstly, the important value of Delphi proposed by experts was optimized by parabolic OWA, and the importance value can be changed adaptively according to the size of the expert score value. Secondly, the weight of the whole index was weighted by entropy weight method, and the grey correlation degree of entropy weight was obtained according to the given optimal resolution coefficient . Finally, the best scheme was selected by ranking the degree. In this paper, a set of typical index system of distribution network planning was given, and the decision-making result of this method in this paper is compared with previous works. The case study verified that this method has the characteristics of simple computation and good fusion of both subjective and objective, which can be used in practice to some extent.

1. 引言

配电网规划是城市配电网规划的主要组成部分，其主要流程包括城市电力负荷预测、变电站选址定容、配电网络规划、无功优化及自动化配置 [1] 。配电网规划方案则是着眼于不同等级变电站容量的确定、配电设备选取以及线路的长度、半径、数量的筛选等 [2] 。优良的配电网规划方案有利于进一步精准投资，传统规划中大多只考虑经济性、可靠性等单一因素，并且只给出一种规划方案，这种追求单一目标的最优必然会以牺牲其它目标为代价，且规划中由于城市区域地形、电源点选择、资金构成、甲方要求、建设期限等不同，理论规划与实际往往不能准确对应，因此目前则是更多地考虑可适应性、环境影响等多种因素，并通过设计出若干个配电网规划方案作综合分析与比较，最终确定一个综合、科学、合理的规划方案，这就要求将综合决策理论引入到配电网规划方案中。

所谓综合决策就是将多个互有竞争力的方案按照一定的方法完成不同属性上的定量与定性的评价，再根据评价结果进行排序与寻优的过程 [3] 。目前配电网方案综合决策方法相比输配电网理论成熟度低 [4] [5] [6] ，主要有层次分析法、模糊评价法以及逼近理想解法等 [7] [8] [9] 。文献 [10] 采用区间层次分析法对判断矩阵的取值区间化，使指标模糊度与专家意见更加契合，将决策中信息的不确定性进一步降低，但方案权重和属性权重根本上还是依赖于主观建立的判断矩阵计算得来的。文献 [11] 采用结构熵权与层次灰色关联度方法进行配电网规划方案综合决策，减少了专家初始排序意见由于主观赋值带来的不确定性，使意见具有一致性收敛，保持了良好的客观性。文献 [12] 用区间层次分析法的优点将传统TOPSIS进行改进，改善了单一的点值序列无法充分体现配电网规划方案决策多样性的缺点，但是文中将定性和定量指标统一打分处理，弱化了定量数据原本的客观性。文献 [13] 采用加强数据包络法改进了传统DEA只能将所有决策单元分为有效和非有效两大类的缺点，根据综合产出与综合投入的比值率高低实现了多决策单元的排序寻优，且无需数据的无量纲处理，客观程度较强。主成分分析法以及神经网络等智能算法虽然在规划中有很强的非线性寻优能力，但所需数据量庞大导致在方案决策中适应度不高 [14] [15] [16] 。综上，将主客观特性良好融合决定着配电网规划综合决策的准确性，其中关键是对指标定性、定量的科学处理。

据此，本文通过采用抛物线OWA对德尔菲中的专家重要度进行赋值来优化定性指标的综合分值，形成对不同规划方案定性指标的单独定量处理，然后再和其余定量指标一同用熵权法赋权，最终根据熵权灰色关联度大小完成排序和决策。此外还给出了适应不同专家量值差异度的不同抛物线OWA权重值，为今后决策工作减少工作量。

2. 抛物线OWA理论

2.1. 抛物线OWA原理

OWA算子 [17] 于1988年被Yager提出之后被广泛应用于管理、神经网络、数据挖掘、图像处理、人工智能、专家系统等诸多领域 [18] [19] ，该算子在决策分析中就权重计算得到了广泛的应用。

设OWA： $R^n\to R$ ，

$\text{OWA}\left(a_1,a_2,L,a_n\right)={\displaystyle \underset{j=1}{\overset{n}{\sum }}{w}_j{b}_j}$ (1)

其中 $a_j$ 是决策指标数据， $w={\left(w_1,w_2,\cdots ,w_n\right)}^{\text{T}}$ 是与OWA相关联的加权向量， $w_j\in \left[0,1\right]$ ， $j=1,2,\cdots ,n$ ，

${\displaystyle \underset{j=1}{\overset{n}{\sum }}{w}_j}=1$ ，且 $b_j$ 是一组数据 $\left(a_1,a_2,L,a_n\right)$ 中第j大的元素，R为实数集，则称函数OWA是有序加权平均

算子。该算子的特点是把决策者的评价信息按大小排序并与权重值相乘，但由于两者对应关系不明确使得评价方向过于离散，最终导致结果严重失真。

抛物线OWA [20] 是将抛物线函数曲线特点与OWA核心思想结合，先按照要求给出相应具体抛物线函数方程，再根据方程求出目标权值，最后将其与事先排列好的决策指标信息相乘得到综合决策值。

考察抛物线方程 $y=1-\frac{x^2}{2p}\left(p>0\right)$ ，它是一条经过 $\left(-\sqrt{2p},0\right)$ ， $\left(0,1\right)$ ， $\left(0,\sqrt{2p}\right)$ 三点、开口向下且关于y轴对称的曲线，基于抛物线函数 $y=1-\frac{x^2}{2p}\left(p>0\right)$ 给出OWA算子的权重为：

$w_j=\frac{1-\frac{{\left(\frac{2j-n-1}{n+1}\right)}^2}{2p}}{{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left(1-\frac{{\left(\frac{2j-n-1}{n+1}\right)}^2}{2p}\right)}}=\frac{2p-{\left(\frac{2j-n-1}{n+1}\right)}^2}{{\displaystyle \underset{j=1}{\overset{n}{\sum }}\left(2p-{\left(\frac{2j-n-1}{n+1}\right)}^2\right)}}$ (2)

2.2. 抛物线OWA性质

由文献 [20] 可知，抛物线OWA具有以下性质：

性质1算子权重有良好的对称性，即 $w_j=w_{n+1-j}$ ；

性质2

当n为奇数时，该OWA算子的权重满足：

$w_1<w_2<\cdots <w_{\frac{n-3}{2}}<w_{\frac{n-1}{2}}<w_{\frac{n+1}{2}}>\cdots >w_n$

当n为偶数时，该OWA算子的权重满足：

$w_1<w_2<\cdots <w_{\frac{n-3}{2}}<w_{\frac{n-1}{2}}<w_{\frac{n+1}{2}}>\cdots >w_n$

性质3 $orness\left(w\right)=0.5$ ，它表示与最大值接近程度的测度算子。

3. 配电网规划方案综合决策体系

3.1. 抛物线OWA熵权–灰色关联度模型的提出

传统的综合评价模型中大多数未将定性指标作单独预处理，通过使用德尔菲法 [21] 可将多数专家对指标的评价结果加权统一，但仅仅根据与同一分数对应的专家人数作为重要度的加权因子虽在一定程度上得到了专家们的主观意见，但是当专家们量值趋于分散时，既会导致加权结果在原有分数上的不收敛，且极端分值的误差影响加大，因此本文提出用抛物线OWA来改进德尔菲中的专家重要度的赋权，从而改善传统德尔菲的不足，并且无需重复统计意见，大大减少了工作量。因此将该方法与传统的熵权–灰色关联分析相结合，得到了主客观良好融合的决策结果。该模型的表达式为：

$\{\begin{array}{l}{b}_{ij}={\displaystyle \underset{k=1}{\overset{p}{\sum }}{w}_k{a}_k}\\ p_{ij}=\frac{b_{ij}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{b}_{ij}}}\\ E_j=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{p}_{ij}\ln p_{ij}}}{\ln n}\\ w_j=\frac{1-E_j}{{\displaystyle \underset{j=1}{\overset{M}{\sum }}\left(1-E_j\right)}}\\ {\xi }_i\left(k\right)=\frac{\Delta \min +\rho \Delta \max }{{\Delta }_i\left(k\right)+\rho \Delta \max }\\ {\gamma }_i={\displaystyle \underset{k=1}{\overset{M}{\sum }}{w}_k{\xi }_i\left(k\right)}\end{array}$ (3)

其中，p是参与打分的专家人数，n是待决策配电网规划方案个数，M是所有的指标个数，m是定性类指标个数， $a_k$ 代表第k个专家的量值， $w_k$ 代表第k个专家的重要度， $b_{ij}$ 是第i个方案中第j个指标的规范前评价值， $p_{ij}$ 是规范后的评价值， $E_j$ 代表第j个指标的熵， $w_j$ 代表第j个指标的权重， ${\xi }_i\left(k\right)$ 代表第i个方案中第j个指标的关联系数， $\rho$ 是取值为[0, 1]的分辨系数， $\Delta \min$ 、 $\Delta \max$ 分别代表待评价方案与最优方案之间对于不同指标的最大、最小距离，要注意的是： $b_{ij}$ 中 $j=\left(1,2,\cdots ,m\right)$ ， $p_{ij}$ 中 $j=\left(1,2,\cdots ,M\right)$ ，其目的是对定性指标单独进行抛物线OWA预处理，再和所有指标一起标准化。

3.2. 指标体系的建立

配电网规划方案指标体系要能充分体现配电网效益的各个方面，优良、科学的指标评估体系决定着评估的模型选择、流程步骤、繁琐程度以及结果准确度，在全方面考虑不同属性要素基础上，按相应权重整合计算得到综合效益值，最终达到对不同规划方案的最优决策。本文建立了表征配电网规划方案综合效益的三级指标体系，选取了体现配电网规划方案可靠性、经济性、环境性与适应性的18个三级指标，如图1所示，该指标体系可以良好的反映规划方案的科学程度。

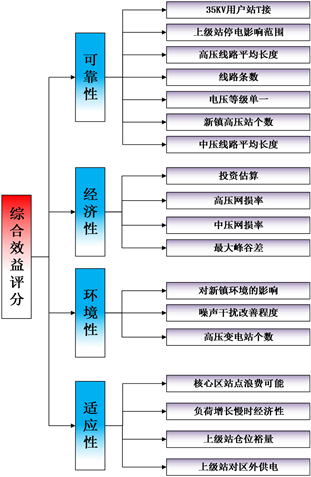
Figure 1. Comprehensive benefit Evaluation Index system of Distribution Network Planning Scheme

图1. 配电网规划方案综合效益评价指标体系

3.3. 指标的预处理

分析指标体系可知，由于配电网规划方案是由建设前通过专家根据往年数据与经验拟定而成，故诸如规划后短路电流、电压合格率等实际运行指标无法取得，因此定性指标数量和种类相比定量指标要多，有利于充分发挥本文方法的优势。文中高、低压线路平均长度、高压站个数、投资估算、高压网损率、中压网损率、新镇高压站个数、高压变电站个数8个指标为定量指标，其余10个指标均为定性指标。

根据抛物线OWA的定义，首先定义所有定性指标的重要度级数和对应的量值，然后针对各个定性指标通过德尔菲法统计所有专家给出的量值，并对比不同专家的量值区分度大小来赋予不同的抛物线p值，最后基于抛物线OWA法计算得到不同指标的综合得分。定性数据的量化度表如表1所示，其中考虑到如“核心区站点浪费可能”、“上级站对区外供电”等指标属于逻辑型评价指标，为减小误差这里用10⁻⁵代替0来定义此类指标的量化度。

Table 1. Quantifications of qualitative indicators

表1. 定性指标的量化度

现在计算一下专家重要度，假设存在8个专家，则根据公式(2)， $n=8$ ，当对p取不同值时，通过计算得 $w_j$ 取值如下：

$p=0.25$ 时， $w_j=\left(-0.0545,0.0994,0.2019,0.2532,0.2532,\mathrm{0.2019.0.0994},-0.0545\right)$

$p=0.5$ 时， $w_j=\left(0.0667,0.1167,0.1500,0.1667,0.1667,\mathrm{0.1500.0.1167},0.0667\right)$

$p=1$ 时， $w_j=\left(0.1002,0.1215,0.1356,0.1427,0.1427,\mathrm{0.1356.0.1215},0.1002\right)$

$p=2$ 时， $w_j=\left(0.1134,0.1233,0.1300,0.1333,0.1333,\mathrm{0.1300.0.1233},0.1134\right)$

由此可见，当p越来越大时，所求的各项权重值逐渐相似，越往中间靠拢权重值越大且呈左右对称分布，与前面所述抛物线OWA性质相符，当各个专家所给出的量值比较分散，跨度较大时，通过相应取较大的p值降低极端分值的效应，使最终分值向中间收敛。

3.4. 综合决策的步骤

根据本文提出的综合决策模型所确定的具体决策步骤如下：

1) 选取待决策的n个目标配电网规划方案；

2) 建立表征配电网的综合效益的指标体系；

3) 收集整理指标数据，根据专家查阅历史数据根据要求拟定定量指标数据，定性指标则先收集各专家的打分量值；

4) 抛物线OWA求取各专家重要度，进行定性指标预处理；

5) 熵权法求取定性、定量指标权重；

6) 灰色关联分析求取各指标关联系数；

7) 加权得到熵权–灰色关联度并排序、决策。

具体流程如图2所示：

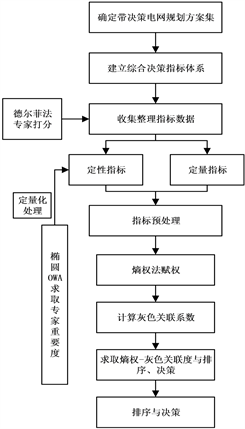
Figure 2. Comprehensive decision flow chart of distribution network planning scheme

图2. 配电网规划方案综合决策流程图

4. 实例分析

本文选取上海某规划区为例验证提出的综合决策模型的有效性。该规划区规划范围包括全区高压配电网规划、核心区及新镇一期中压配电网规划 [22] [23] [24] ，待决策规划方案有三个：35 kV、110 kV及35 kV~110 kV混合方案。通过收集、整理得到指标数据如表2所示，其中35 kV用户站T接、噪音干扰改善程度等10个定性指标已通过抛物线OWA处理得到最终评价值，并且各个方案均满足N − 1条件下最低电压，过负荷等技术约束。

Table 2. Data sheet of different power network planning schemes

表2. 不同电网规划方案数据表

根据表2中的数据，运用抛物线OWA熵权–灰关联模型进行求解，将得到的熵权–灰色关联度取值进行排序，其中灰色关联分析中分辨系数取 $\rho =0.69$ ，由文献 [25] 得该值为去除主观性因素的最优取值，并将综合排序结果分别与之前所做的SE-DEA模型、区间层次法、模糊层次分析进行对比，如表3所示。

由表3可知，方案3与理想方案的关联度最大，方案2次之，方案1最差，因此最终选择方案3为最优决策，该方法结果与区间层次分析、模糊层次分析相一致，与SE-DEA模型决策结果也相差无几。

通过该案例可以看出，抛物线OWA赋权方法并没有彻底抹消决策过程中专家主观赋予的最大量值与最小量值的作用，而是赋予它们较小的权重而使决策结果收敛，使之尽量保持决策的主观性，同时结合熵权–灰关联的客观综合决策方法将使决策结果更加科学。

Table 3. Comprehensive decision ranking

表3. 综合决策排序

5. 结论

本文提出抛物线OWA熵权–灰关联的综合决策方法，并在配电网规划方案中应用，具体工作如下：

1) 构建了含有四个维度、16个指标的配电网综合效益评估指标体系，较完整地体现了表征配电网规划方案综合效益的各个因素，并给出了具体的决策实例。

2) 详细分析了指标数据类型的特点，将抛物线OWA应用到德尔菲专家评价法中，有效、简便地将指标体系中的定性指标定量化，既保留了专家们的主观因素，同时缩小了由主观极端值带来的数据误差，不同的抛物线p值使定性指标评价结果得到有效收敛，提高了指标预处理的准确性。

3) 本文采用熵权–灰色关联分析方法对配电网规划方案进行综合决策，确保了决策过程的客观性，发挥了其在小样本数据处理中的优势，通过算例表明该方法结果上和其他方法保持一致，验证了该方法的有效性。

在下一步研究中，需要进一步加强对专家量值梯度的分解和抛物线p值自适应调整，使未来结果更加精确；另一方面是否有比抛物线更有优化特性的其他函数曲线有待探索。