考虑个性化驾驶员的信号口车速引导研究

A Study of Speed Guidance at Signal Gates Considering Individualized Drivers

摘要: 车速引导系统的发展可以减少道路交通拥堵现象，保证行车安全，提高通行效率与燃油经济性，但针对个性化驾驶员的车速引导以及跟驰状态下的车速引导研究甚少，多为考虑单车的路口通行引导，且现有的车速引导系统研究中大多忽视不同驾驶风格的主观决策对车速引导的影响，车速引导系统缺乏广泛的适用性，难以满足不同类型驾驶员的需求。因此本文建立在对驾驶员驾驶风格分类的基础上，利用层次分析法(AHP)分别对不同风格的驾驶员进行路口通行时的决策倾向指标进行权重确定，将跟驰模型与车速引导相结合，优化跟驰模型，得出最优引导加速度，通过仿真得出优化曲线，研究表明，在考虑了个性化驾驶员的跟驰行为后的车速引导模型，能在保证一定的车辆通行效率的前提下，提高了安全性，更加符合现实驾车场景，具有一定的参考价值。

Abstract: The development of speed guidance system can reduce road traffic congestion, ensure traffic safety, and improve traffic efficiency and fuel economy, but there is little research on speed guidance for individual drivers and speed guidance in the following state, mostly considering the intersection guidance of a single vehicle, and most of the existing speed guidance system research ignores the impact of subjective decisions of different driving styles on speed guidance, and the speed guidance system. The speed guiding system lacks wide applicability and is difficult to meet the needs of dif-ferent types of drivers. Therefore, this paper builds on the classification of drivers’ driving styles, uses the hierarchical analysis method (AHP) to determine the weights of the decision tendency in-dicators of drivers with different styles when making intersection passes respectively, combines the following model with the speed guidance, optimizes the following model to derive the optimal guidance acceleration, and derives the optimization curve through simulation. The study shows that the speed guidance model after considering the individual driver’s following behavior can improve the safety and meet the realistic driving scenario with certain reference value, while ensuring cer-tain vehicle passing efficiency.

1. 引言

为实现更加环保、绿色地通行，响应国家的政策，汽车成为了首当其冲需要改进的对象，而信号口是交通安全问题与污染排放的重地，随着互联网技术与智能交通的发展，车速引导系统的出现不仅能缓解上述问题，更能提高能源的利用效率增大路口的通行率。当下学者对车速引导系统的研究的重点各不相同：李振龙等人 [1] 从驾驶员与引导速度的博弈决策层面出发，突破了车速引导模型中驾驶员完全遵从引导速度的理想假设，提出了有限理性下的车速引导模型，这种考虑实际情况的模型可为车速引导系统的实际应用提供参考；王文辉等人 [2] 以三角函数优化的车速引导模型为基础，考虑到驾驶员在实际驾驶时无法完全跟踪速度引导曲线，设计了一种闭环反馈速度更新算法，动态补偿了人车响应特性造成的跟踪偏差，增强了车速引导系统对驾驶员的适应性；Tang T Q等人 [3] 将速度引导策略引入到汽车跟踪模型中，研究了具有多个信号交叉口的单车道道路的驾驶行为和燃油消耗；Zejian Deng等人 [4] 引入了驾驶员实际选择的速度与理论曲线速度之比的与驾驶员驾驶风格相关的驾驶员行为影响因子，对曲线速度模型进行改进，根据驾驶员的驾驶风格提供不同的合适的曲线安全速度。

综上文献所述，不足点在：1) 虽然已经出现考虑驾驶员的影响而非单单着重汽车本身的动力学的研究，但在结合时，车速控制模型依旧以考虑单车为主；

2) 考虑跟驰模型与车速引导的结合但缺少对个性化驾驶员的影响与需求分析；

3) 闭环反馈的车速引导模型过于简单，缺乏考虑对不同驾驶风格的驾驶员的影响分析。

因此，针对上述问题，以将跟驰模型与车速引导相结合为目标，对不同风格的驾驶员在路口通行时的决策权重进行确定，利用不同风格驾驶员的反应灵敏度不同，优化跟驰模型，得出优化后的实际最优加速度进行符合个性化驾驶员的车速引导需求。

2. 个性化驾驶员通行决策的权重确定

2.1. 层次分析法

层次分析法(AHP) [5] 是一种基于专家打分的主观定量分析方法，通过递进式层状结构来确定每个指标的权重，一般分为三个步骤：1) 构建层状结构；2) 构造判断矩阵；3) 一致性检验。层次分析法的具体操作以及计算需求内容如下：

1) 构建层状结构

一般将层状结构分为：目标层、指标层、方案层，共三层，对每个指标做出主观权衡，得出方案。

2) 构造判断矩阵

判断矩阵的形成是为了将矩阵内的元素每两两进行主管比较从而得到不同的权重分配，假设判断矩阵为A，矩阵内的各个元素为 $a_{ij}$ ，其代表了第i个元素与第j个元素相比，其重要程度的展示，定义的矩阵A以及权重分配比例表如表1所示：

$A_{n\times n}=\left[\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& \ddots & ⋮\\ a_{n1}& \cdots & a_{nn}\end{array}\right]$ (1.1)

Table 1. Weight proportion distribution table

表1. 权重比例分配表

3) 一致性判断

由于在处理层次结构时过于繁琐，在实际运用时，定义了一致性比率值CR同时引入一致性检验标准CI对所构建的判断矩阵进行一致性检验，比率值CR的计算公式如下：

$\text{CR}=\frac{\text{CI}}{\text{RI}}$ (1.2)

其中RI的值可以通过矩阵的阶数查表获得：

Table 2. Value of consistency index RI

表2. 一致性指标RI的值

所引入的一致性检验标准CI的计算公式如公式(1.3)所示：

$\text{CI}=\frac{{\lambda }_{\max }-n}{n-1}$ (1.3)

其中 ${\lambda }_{\max }$ 为判断矩阵A的最大特征值，n为判断矩阵A的阶数；CI的值越大，判断矩阵的一致性越差，而对于公式(1.2)中的一致性比率CR，其值不可以大于0.1，若大于，则判断矩阵的一致性不符合要求，需要对判断矩阵进行重新构建。 ${\lambda }_{\max }$ 的计算公式如公式(1.4)所示：

${\lambda }_{\max }={\displaystyle {\sum }_{i=1}^n\frac{{\left(A\omega \right)}_i}{n{\omega }_i}}$ (1.4)

式中 $\omega$ 的值需要对构造的判断矩阵按列归一化后取行均值得出。

2.2. 个性化驾驶员决策权重计算

根据研究学者分析 [6] [7] ，将驾驶员的通行整合数据通过K-means算法分为三类最为科学分别为：激进型驾驶员、普通型驾驶员以及保守型驾驶员，这三类驾驶员在信号口跟车决策通行时，侧重点各不相同，运用层次分析法为每类驾驶员构造判断矩阵并分别对其进行权重确定。

1) 激进型驾驶员

激进型驾驶员在交通信号灯引导下的路口通行时，面对跟车场景，更容易忽视合适的跟车距离与燃油消耗，以通过路口为主要目标，其速度均值与冲击度都要高于普通型驾驶员与保守型驾驶员。因此，针对以上特点，以跟车距离、燃油消耗量和通行时间作为决策权衡指标，所构造的判断矩阵为：

$A_{agg}=\left(\begin{array}{ccc}1& 3& 1/6\\ 1/3& 1& 1/8\\ 6& 8& 1\end{array}\right)$ (1.5)

按列对激进型驾驶员的判断矩阵进行归一化处理得：

$A_{agg}=\left(\begin{array}{ccc}0.1364& 0.2500& 0.1290\\ 0.0455& 0.0833& 0.0968\\ 0.8182& 0.6667& 0.7742\end{array}\right)$ (1.6)

对同一行的数据取均值得到 $\omega ={\left(\begin{array}{ccc}0.1718& 0.0752& 0.7530\end{array}\right)}^{\text{T}}$ ，分别对应激进型驾驶员对跟车距离、燃油消耗量和通行时间的权重，根据公式(1.4)可以求得 ${\lambda }_{\max }^{agg}=3.0749\ge n$ ，符合要求。查表2得知，三阶矩阵的RI值为0.58，再根据公式(1.3)可以求得CI值为0.0374，最后利用公式(1.2)求出比率值CR = 0.0646 < 0.1，因此所构造的激进型驾驶员的判断矩阵符合一致性要求。

2) 保守型驾驶员

而对于保守型驾驶员在交通信号灯引导下的路口通行时，更加会考虑安全性，尤其是处于跟驰状态下时，保证合适的跟车距离的前提才会考虑通过性以及燃油消耗等问题。其速度均值与冲击度在三类驾驶员中都处于最低值。因此，针对以上特点，所构造的判断矩阵为：

$A_{con}=\left(\begin{array}{ccc}1& 9& 6\\ 1/9& 1& 1/4\\ 1/6& 4& 1\end{array}\right)$ (1.7)

按列对激进型驾驶员的判断矩阵进行归一化处理得：

$A_{con}=\left(\begin{array}{ccc}0.7826& 0.6429& 0.8276\\ 0.0870& 0.0714& 0.0345\\ 0.1304& 0.2857& 0.1379\end{array}\right)$ (1.8)

对同一行的数据取均值得到 $\omega ={\left(\begin{array}{ccc}0.7510& 0.0643& 0.1847\end{array}\right)}^{\text{T}}$ 。根据公式(1.4)求得 ${\lambda }_{\max }^{con}=3.1107\ge n$ ，符合要求。根据公式(1.3)可以求得CI值为0.0554，最后利用公式(1.2)求出比率值CR = 0.0955 < 0.1，因此所构造的保守型驾驶员的判断矩阵符合一致性要求。

3) 普通型驾驶员

最后对普通型驾驶员通过路口的决策进行分析，普通型驾驶员在交通信号灯引导下的路口通行时，对于安全性的考虑相较于燃油消耗和通过性优先级要大。在保证一定的安全前提下，尽可能可以通过路口而后才会考虑燃油消耗问题。其速度均值与冲击度的大小在三类驾驶员中处于中间位置。因此，针对以上特点，所构造的判断矩阵为：

$A_{ord}=\left(\begin{array}{ccc}1& 6& 3\\ 1/6& 1& 1/5\\ 1/3& 5& 1\end{array}\right)$ (1.9)

按列对激进型驾驶员的判断矩阵进行归一化处理得：

$A_{ord}=\left(\begin{array}{ccc}0.6667& 0.5000& 0.7143\\ 0.1111& 0.0833& 0.0476\\ 0.2222& 0.4167& 0.2381\end{array}\right)$ (1.10)

对同一行的数据取均值得到 $\omega ={\left(\begin{array}{ccc}0.6270& 0.0807& 0.2923\end{array}\right)}^{\text{T}}$ 。根据公式(1.4)求得 ${\lambda }_{\max }^{ord}=3.0952\ge n$ ，符合要求。根据公式(1.3)可以求得CI值为0.0476，最后利用公式(1.2)求出比率值CR = 0.0821 < 0.1，同样构造的普通型驾驶员的判断矩阵符合一致性要求。

对于上述三种类型风格的驾驶员对跟车距离、燃油消耗量以及通行时间的权重 $\omega$ 分析可知：相较于保守型驾驶员，激进型驾驶员在路口通行时更加注重通行效率，即会以更高的车速跟车行驶，且过程中速度变化率较大，容易忽视车速引导系统建议的合理车速，一旦前方车辆紧急制动，容易产生安全问题。而保守型驾驶员过于注重通行的安全性，可能在跟驰环境下无法在剩余的交通指示灯时间内通过路口，行车速度较慢，速度变化较小，容易影响车道的通行效率引起交通堵塞等问题。其中通行时间的权重差别最为明显，即车道内行驶速度差异较大，而驾驶员对外界刺激的敏感程度与速度是成正相关。因此，在后文对引入跟驰行为的车速引导模型的优化中，以敏感系数作为表征不同驾驶风格的指标，优化车速引导模型，提高模型的现实场景适用性。

3. 跟驰模型优化

3.1. 基于车速引导的跟驰模型优化

跟驰模型经常被用于研究车辆控制部分，传统的跟驰模型大多用于分析驾驶员的主观行为与车道通行的影响关系问题。而随着智能汽车与车路协同的发展，车速引导系统会影响甚至改变驾驶员的驾驶操作以及车辆的跟车行为，在加上交通信号机的影响 [8] ，因此对于传统车辆在车道内的跟驰模型需要做出优化。本文以FDV跟驰模型 [9] [10] 为基础，将后车视为车速引导系统的引导对象，考虑前车的运动状态信号灯的状态，以引导后车与前车以同样的车速通过路口为目标，考虑车速引导系统的跟驰模型改进为：

$a_o=\frac{\text{d}{v}_o\left(t\right)}{\text{d}t}=f\left(\alpha \right)\left[v_a^{obj}-v_o\left(t\right)\right]+\beta \Delta v\left(t\right)$ (2.1)

式中： $a_o$ 为后车的跟驰加速度， $v_o\left(t\right)$ 为t时刻后车的速度， $v_a^{obj}$ 为前车的目标车速， $\Delta v\left(t\right)$ 为t时刻前后辆车的速度差， $f\left(\alpha \right)$ 为驾驶员的敏感系数； $\beta$ 为反馈系数，取值为0.3 s⁻¹。

3.2. 基于不同驾驶风格的跟驰模型优化

在上述的跟驰模型中，用 $f\left(\alpha \right)$ 表示为驾驶员的敏感系数函数 [11] ，由于驾驶员驾驶风格不同，其对于外界刺激的敏感程度不同，而在许多研究中将 $f\left(\alpha \right)$ 确定为固定常量，过于理想化不符合实际。根据第一节的研究，不同风格驾驶员路口通行的权重不同，其中通行时间的差异最大，激进型驾驶员为了提高路口通行效率，其平均速度以及速度变化率会比保守型驾驶员要大，也因此激进型驾驶员会提高警觉，敏感程度要大于保守型驾驶员，因此本文以敏感系数作为表征不同驾驶风格驾驶员的指标。

由于不同风格驾驶员对外界的灵敏程度与速度的大小有关，且成正比例关系，但由于人类反应程度的有限性 [12] ，因此需要将敏感系数的值控制在合理范围内，并对不同驾驶风格驾驶员的敏感系数做出取值范围划分。在此利用sigmoid函数构建动态敏感系数函数 $f\left(\alpha \right)$ 如下所示：

$f\left(\alpha \right)=\alpha \left({\alpha }_1+\frac{{\alpha }_2}{1+{\text{e}}^{k\left(v_{ave}-v\right)}}\right)$ (2.2)

其中 $\alpha$ 、 ${\alpha }_1$ 、 ${\alpha }_2$ 与k为未知常系数， $v_{ave}$ 为车道平均速度，v表示被引导车辆当前车速。根据公式(2.1)，最终考虑不同驾驶风格结合跟驰模型 [13] 的车速引导模型为：

$a_o=\frac{\text{d}{v}_o\left(t\right)}{\text{d}t}=\alpha \left({\alpha }_1+\frac{{\alpha }_2}{1+{\text{e}}^{k\left(v_{ave}-v\right)}}\right)\left[v_a^{obj}-v_o\left(t\right)\right]+\beta \Delta v\left(t\right)$ (2.3)

驾驶员在以高于车道车辆平均速度的速度行驶时，反应较为敏感，能够更快的对前车速度的突然变化做出反应，而在以低于车辆平均速度的速度行驶时，反应较不敏感。根据学者实验研究发现 [14] ，在平均车速为15 m/s的车道上， $f\left(\alpha \right)$ 的变化程度在车速小于10 m/s时变化较小，取值在1左右；速度区间在10 m/s到20 m/s时， $f\left(\alpha \right)$ 变化程度剧烈，并在车速为20 m/s时达到最高值2.3，也为实验结果的最高驾驶员灵敏度。由于城市道路限速60 km/h，因此 $f\left(\alpha \right)$ 的最大值为2。

对不同风格驾驶员的速度区间进行划分：

$V=\{\begin{array}{ll}\left[50,60\right],\hfill & 激进型驾驶员\hfill \\ \left(40,50\right),\hfill & 普通型驾驶员\hfill \\ \left[30,40\right],\hfill & 保守型驾驶员\hfill \end{array}$ 单位：km/h (2.4)

根据速度区间，对不同驾驶风格驾驶员的敏感系数取值划分如下：

$f\left(\alpha \right)=\{\begin{array}{ll}\left[1.45,2\right],\hfill & 激进型驾驶员\hfill \\ \left(1.02,1.45\right),\hfill & 普通型驾驶员\hfill \\ \left[1,1.02\right],\hfill & 保守型驾驶员\hfill \end{array}$ 单位：S (2.5)

4. 考虑后车个性化驾驶员的车速引导场景分析及其模型构建

4.1. 绿灯场景车速引导模型

当后车进入车速引导范围内，所获取的交通指示灯为绿灯为应用场景，绿灯进入倒计时，需要加速才能通过路口。假设绿灯剩余时间为 $T_{gre}^l$ ，后车离停车线距离为S，后车驾驶员的反应时间为 $t_{act}$ 。前车目标车速 $v_a^{obj}$ 以车道限制最大车速行驶。

1) 后方车辆驾驶员为激进型风格：

激进型驾驶员以通过路口为目标，跟驰距离较短，车速较大，合理车速引导下的跟驰加速度为：

$a_o^{agg}=f_{agg}\left(\alpha \right)\left[v_a^{lim}-v_o\left(t\right)\right]+\beta \Delta v\left(t\right)$ (3.1)

对于激进型驾驶员而言，此时最优加速度为：

$a_{o-best}^{agg}=\min \left(a_o^{agg},a_{\max }\right)$ (3.2)

2) 后方车辆驾驶员为保守型风格：

保守型驾驶员由于自身技术以及谨慎性格等主观性原因影响，其车辆进入车速引导范围内时，容易与前车产生过大的跟驰距离，速度较慢，灵敏较低，跟驰加速度为：

$a_o^{con}=f_{con}\left(\alpha \right)\left[v_a^{lim}-v_o\left(t\right)\right]+\beta \Delta v\left(t\right)$ (3.3)

对于保守型驾驶员而言，此时最优加速度为：

$a_{o-best}^{con}=\max \left(a_o^{con},a_{\max }\right)$ (3.4)

3) 后方车辆驾驶员为普通型风格：

普通型驾驶员为三者中跟驰距离最为适中的，在车辆进入速度引导区范围内时，驾驶员灵敏度适中，其跟驰加速度为：

$a_o^{ord}=f_{ord}\left(\alpha \right)\left[v_a^{lim}-v_o\left(t\right)\right]+\beta \Delta v\left(t\right)$ (3.5)

对于普通型驾驶员而言，此时最优加速度为：

$a_{o-best}^{ord}=\min \left(a_o^{ord},a_{\max }\right)$ (3.6)

对于加速引导场景，则所行驶的总距离 $S_{total}\ge S$ ，即：

$S_{total}\ge t_{act}{v}_o\left(t\right)+\frac{v_a^{lim}{}^{{}^2}-v_o{\left(t\right)}^2}{2a}$ (3.7)

4.2. 红灯场景车速引导模型

当后车进入车速引导范围内，所获取的交通指示灯为红灯为应用场景，但红灯时间进入倒计时，保持车速行驶至路口容易出现交通指示灯依旧是红灯的场景。此时需要引导车辆减速行驶，在到达路口信号前时红灯已经结束且转为绿灯，使车辆保持一定的速度。假设红灯剩余时间为 $T_{red}^l$ ，后车离停车线距离为S，前车以车速 $v_a^{obj}$ 通过路口。

1) 后方车辆驾驶员为激进型风格：

激进型驾驶员在前方车辆减速场景下时，跟驰距离较短，车速较大，需要以更大的减速度进行跟驰，合理车速引导下的跟驰减速度为：

$d_o^{agg}=f_{agg}\left(\alpha \right)\left[v_a^{obj}-v_o\left(t\right)\right]+\beta \Delta v\left(t\right)$ (3.8)

对于激进型驾驶员而言，此时最优减速度为：

$\left|d_{o-best}^{agg}\right|=\min \left(\left|d_o^{agg}\right|,\left|d_{\max }\right|\right)$ (3.9)

2) 后方车辆驾驶员为保守型风格：

保守型驾驶员在其车辆进入车速引导范围内时，由于跟驰距离足够保证安全距离，速度较慢，灵敏较低，跟驰减速度为：

$d_o^{con}=f_{con}\left(\alpha \right)\left[v_a^{obj}-v_o\left(t\right)\right]+\beta \Delta v\left(t\right)$ (3.10)

对于保守型驾驶员而言，此时最优减速度为：

$\left|d_{o-best}^{con}\right|=\min \left(\left|d_o^{con}\right|,\left|d_{\max }\right|\right)$ (3.11)

3) 后方车辆驾驶员为普通型风格：

普通型驾驶员为三者中跟驰距离最为适中的，在车辆进入速度引导区范围内时，驾驶员灵敏度适中，其跟驰减速度为：

$d_o^{ord}=f_{ord}\left(\alpha \right)\left[v_a^{obj}-v_o\left(t\right)\right]+\beta \Delta v\left(t\right)$ (3.12)

对于普通型驾驶员而言，此时最优减速度为：

$\left|d_{o-best}^{ord}\right|=\min \left(\left|d_o^{ord}\right|,\left|d_{\max }\right|\right)$ (3.13)

对于减速引导场景，则所行驶的总距离 $S_{total}\le S$ ，即：

$S_{total}\le t_{act}{v}_o\left(t\right)+\frac{v_a^{abj}{}^{{}^2}-v_o{\left(t\right)}^2}{2d}$ (3.14)

5. 仿真实验分析

5.1. 仿真平台搭建

本文选用carsim软件作为仿真平台，以(2.4)中针对不同驾驶风格驾驶员的驾驶特点而划分的速度区间为依据，进行不同场景的试验。同时，为了方便识别车辆，采用队列思想，当相近两车辆车头时距小于一个标准车头时距时，两车视为一个队列 [15] ，否则不视为同一车队。具体试验参数数值如表3所示：

Table 3. Simulation basic parameter settings

表3. 仿真基本参数设置

5.2. 绿灯场景仿真实验

对与绿灯加速场景，设置仿真试验需要引导后车与前车基于车队形式以相同速度共同通过路口，对于后车不同驾驶风格驾驶员，具体仿真试验如下：

① 对于激进型驾驶员：

根据(2.4)的速度划分区间，取激进型驾驶员绿灯驾驶场景。在carsim软件中的设置仿真内容如下：在工况页面设置仿真时长为10 s、后车距离停车线长度为120 m；在Miscellaneous Data页面设置事件Event，添加控制：当后车车速 $V\ge 60\text{km}/\text{h}$ ，触发事件使速度保持为60 km/h。当设置跟驰平均速度为50 km/h，前车初速度为52 km/h，目标速度取最大值 $V_{\max }=60\text{km}/\text{h}$ ，同时设置两车初始间距为6 m，符合激进型驾驶员的跟驰特点，根据模型公式(3.1)，计算出此时引导加速度 $a_o^{agg}$ 取值为4.1946 m/s² < a_max，此时加速时间为0.662 s，即carsim软件中利用工况produce建立速度–时间控制关系为：在考虑到驾驶员的反应时间为 $t_{act}$ 为2 s时，需要在2.662 s时，引导后车车速提升至60 km/h。

② 对于保守型驾驶员：

同理，取保守型驾驶员绿灯驾驶场景下，在carsim软件中的设置仿真内容如下：在工况页面设置仿真时长为10 s、后车距离停车线长度为120 m；在Miscellaneous Data页面设置事件Event，添加控制：当后车车速 $V\ge 60\text{km}/\text{h}$ ，触发事件使速度保持为60 km/h。当设置跟驰平均速度为38 km/h，前车初速度为52 km/h，目标速度取最大值 $V_{\max }=60\text{km}/\text{h}$ ，同时设置两车初始间距为12 m，符合保守型驾驶员的跟驰特点，根据模型公式(3.3)，计算出此时引导加速度 $a_o^{con}$ 取值为7.2774 m/s² < a_max，此时加速时间为0.840 s，即carsim工况中速度–时间控制需要引导车速在2.840 s时提升至60 km/h。

③ 对于普通型驾驶员：

最后对于普通型驾驶员绿灯驾驶场景下，在carsim软件中的设置仿真内容如下：在工况页面设置仿真时长为10 s、后车距离停车线长度为120 m；在Miscellaneous Data页面设置事件Event，添加控制：当后车车速 $V\ge 60\text{km}/\text{h}$ ，触发事件使速度保持为60 km/h。跟驰平均速度为42 km/h，前车初速度为52 km/h，目标速度取最大值 $V_{\max }=60\text{km}/\text{h}$ 。在carsim软件中进行设置，同时设置两车初始间距为10 m，符合普通型驾驶员的跟驰特点，根据模型公式(3.5)，计算出此时引导加速度 $a_o^{ord}$ 取值为5.9831 m/s² < a_max，此时加速时间为0.836 s，即carsim工况中速度–时间控制需要引导车速在2.836 s时提升至60 km/h。

对于上述三种不同驾驶风格驾驶员在绿灯信号下通行的车速引导，仿真试验结果如图1、图2所示：

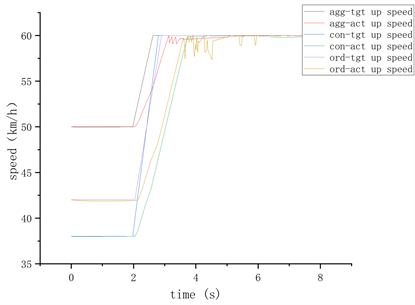
Figure 1. Green light scenario speed-time graph for three driving styles of drivers

图1. 三种驾驶风格驾驶员的绿灯场景车速–时间图

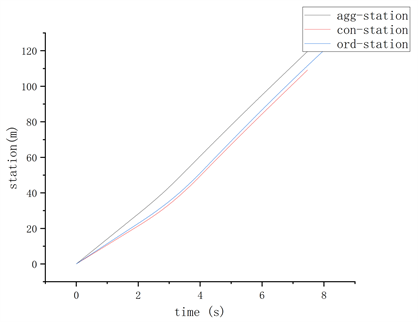
Figure 2. Green light scenario displacement-time diagram for three driving styles drivers

图2. 三种驾驶风格驾驶员的绿灯场景位移–时间图

5.3. 红灯场景仿真实验

在路口红灯倒计时场景下，为了降低能源与车辆机械部件损耗，减少汽车在运行过程中的启停次数，需要引导后车与前车在红灯结束时，恰好以一定的速度不停车通过路口，与绿灯场景仿真试验类似，具体仿真试验过程如下：

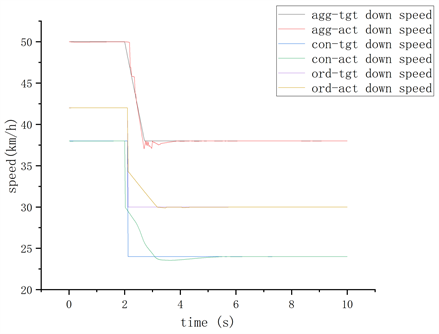
Figure 3. Red light scenario speed-time graph for three driving styles drivers

图3. 三种驾驶风格驾驶员的红灯场景车速–时间图

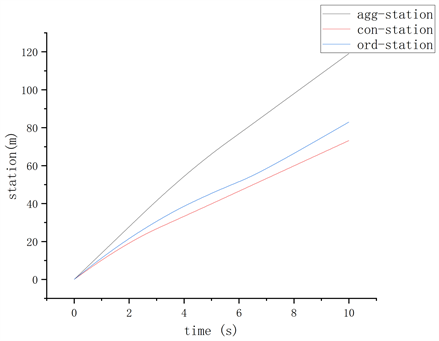
Figure 4. Red light scenario displacement-time diagram for three driving styles drivers

图4. 三种驾驶风格驾驶员的红灯场景位移–时间图

① 于激进型驾驶员：

取激进型驾驶员红灯驾驶场景下，在carsim软件中的设置仿真内容如下：在工况页面设置仿真时长为10 s、后车距离停车线长度为120 m；在Miscellaneous Data页面设置事件Event，添加控制：当后车车速 $V\le 38\text{km}/\text{h}$ ，触发事件使速度保持为38 km/h。当跟驰平均初速度为50 km/h，前车初速度为52 km/h，目标速度 $v_a^{obj}=38\text{km}/\text{h}$ ，同时设置两车初始间距为6 m，符合激进型驾驶员的跟驰特点，根据模型公式(3.8)，计算出此时引导减速度 $d_o^{agg}$ 取值为−4.6667 m/s² > d_max，此时减速时长为0.714 s，即在2.714 s后，需要引导车速减速至38 km/h。而与绿灯场景不同，在剩余红灯时间10 s内，对于激进型驾驶员而言，其减速运行以及后续匀速行驶通过剩余路段的总时间要大于红灯的剩余时间。

② 对于保守型驾驶员：

取保守型驾驶员红灯驾驶场景下，在carsim软件中的设置仿真内容如下：在工况页面设置仿真时长为10 s、后车距离停车线长度为120 m；在Miscellaneous Data页面设置事件Event，添加控制：当后车车速 $V\le 24\text{km}/\text{h}$ ，触发事件使速度保持为24 km/h。当跟驰平均速度为38 km/h，前车初速度为52 km/h，目标速度 $v_a^{obj}=24\text{km}/\text{h}$ ，同时设置两车初始间距为12 m，符合保守型驾驶员的跟驰特点，根据模型公式(3.10)，计算出此时引导减速度 $d_o^{agg}$ 取值为−2.7226 m/s² > d_max，此时减速时长为1.428 s，即在3.428 s后，需要引导车速减速至24 km/h后匀速行驶，可以在到达路口前，红灯结束转为绿灯顺利不停车的以较低速度通过路口。

③ 对于普通型驾驶员：

最后，取普通型驾驶员红灯驾驶场景下，在carsim软件中的设置仿真内容如下：在工况页面设置仿真时长为10 s、后车距离停车线长度为120 m；在Miscellaneous Data页面设置事件Event，添加控制：当后车车速 $V\le 30\text{km}/\text{h}$ ，触发事件使速度保持为30 km/h。当试验设定跟驰平均速度为42 km/h，前车初速度为52 km/h，目标速度 $v_a^{obj}=30\text{km}/\text{h}$ ，设置两车初始间距为10 m，符合普通型驾驶员的跟驰特点，根据模型公式(3.12)，计算出此时引导减速度 $d_o^{agg}$ 取值为−2.6005 m/s² > d_max，此时减速时长为1.282 s，即在3.282 s后，需要引导车速减速至24 km/h后匀速行驶，可以在到达路口前，红灯结束转为绿灯顺利不停车的以较低速度通过路口。

对于上述三种不同驾驶风格驾驶员在红灯信号下通行的车速引导，仿真试验结果如图3、图4所示。

6. 结论

对比第五部分仿真试验图1~4：在绿灯加速场景，在设定符合不同驾驶风格驾驶员的车速条件以及跟驰距离条件下，仿真结果表明，根据本文所提出的基于跟驰模型并考虑不同驾驶风格驾驶员的信号口车速引导模型所得出的引导加速度，能够在剩余绿灯时间为内，引导后车以目标速度同前车一同加速通过路口；同理，在红灯减速通行路口，根据模型所得到的引导减速度，可以引导车辆在到达路口前，信号灯已经变为绿灯，使车辆减速但不停车地通过路口。

综上可知：本文所提出的车速引导模型，在车路协同的交通环境下对个性化驾驶员有着良好的适用性，可以成功的引导车辆以当前场景下最合适的加/减速度顺利通过交通信号口，相比较传统的车速引导模型，更加符合现实驾车场景，具有一定的工程价值。

7. 结束语

本文的试验以及模型，是在一定的假设前提下完成的，针对不同驾驶风格驾驶员最有可能的行驶速度以及跟驰行为进行模型的建立以及仿真工况的设置，具体的完成内容以及不足如下：

文本在基于FVD跟驰模型的基础上，将信号口车速引导与之结合，并同时考虑了后车驾驶员的驾驶风格对跟驰模型的影响。在引导过程中，采用了列队组合思想，诱导后车与前车以同样的速度通过路口。根据仿真结果图表明，在考虑了后车驾驶员不同驾驶风格后，车速引导模型能更有针对性地去适配不同驾驶员的要求，实现模型的定制化与个性化，大大提高了路口的通行效率，降低了信号口的车辆启停次数，减少能源损耗。

本文不足点：在对驾驶员敏感系数以及符合驾驶风格的车速确定时，还不够精确，只能给定一个估值范围；同时，本文研究的是单信号口的通行，缺少对多信号口个性化驾驶员的车速引导研究。

在后续的研究中，会继续对模型进行选择和优化，同时考虑车辆在多信号口的驾驶工况，使车速引导能够适应多样化的驾驶场景。