1. 引言
2020年10月16日召开的中共中央政治局提出:“成渝地区双城经济圈的建设有利于形成优势互补、高质量发展的区域经济布局,是构建以国内大循环为主体、国内国际双循环相互促进的新发展格局的一项重大举措”。2021年10月20日,《成渝地区双城经济圈建设规划纲要》发布,并成为了成渝双城经济圈建设的纲领性文件以及制定相关规划和政策的重要依据,势必要将其打造为国家第四个重要经济圈,在西部形成高质量发展的重要增长极,如今关于两地经济产业的联系和联合发展越来越深入,由此两地的产业关联以及相关效应的研究也越来越得到重视。本文运用两区域投入产出模型对成渝两地产业关联进行分析的同时,也将其具体分解为地区间产业溢出效应和反馈效应进行分析和测算,提出相关的政策建议的同时以求进一步推动成渝地区双城经济圈的建设发展。
2. 两区域投入产出模型
区域间投入产出模型由Isard于1951年提出,是要素流量矩阵形式,先是计算区域间的数据流量,再与区域投入产出模型相结合,既包括区域内各部门产品流动状况,也包括区域间各部门产品流动状况。Miller (1963) [1] 则对其进行了改进,进一步测度不同地区间的经济反馈效应。提出两区域投入产出模型:
(1)
式(1)的
为区域r内的直接消耗系数矩阵;
是区域t与r之间直接消耗系数矩阵;不同矩阵中的元素则分别表示区域内和区域间的部门间产品直接消耗数量;
、
分别代表区域1和区域2的最终产品;
、
分别代表区域1和区域2的总产出。中间产品加最终产品之和,即得出总产品。
Round (1985) [2] 提出里昂惕夫逆矩阵并进整理和更改,简写为:
(2)
其中:
(3)
(4)
(5)
(6)
(3)式中的
为区域1的里昂惕夫逆矩阵,表示区域1的乘数效应;(5)式中的
表示为区域2对区域1的溢出效应;(6)式中的
表示为区域1的反馈效应。两区域间各自的溢出效应相乘得出的
代表总产出变化的相互影响。由此得出的
表示包含直接影响和间接影响的全部反馈效应。
根据以上分析的基础,对模型进行乘法分解:
(7)
进一步进行分解:
(8)
以上三个部分则分别为区域内的乘数效应的测度、区域间的溢出效应的测度和区域间的反馈效应测度。其中反馈效应既包括了本地的变化又包括了区域2的变化。
(2007) [3] 将其进一步改进得出:
(9)
(10)
(11)
公式(11)表示区域间反馈效应,并且已排除了区域内的乘数效应。
求和算子表示为
,对表示各效应矩阵的各列向数值求和,可得到区域间溢出效应和反馈效应。对区域间溢出效应和区域间反馈效应进行后向测度,得出测度矩阵如下 [4] :
区域间溢出效应为:
(12)
区域间反馈效应为:
(13)
式(12)和(13)中的
和
都为1 × n行向量,其中元素
表示r地区j部门最终产出的变化对t地区总产出的影响,元素
表示r地区j部门最终产出的变化引起t地区总产出变化反过来引起的本地区总产出带来的变化。
3. 数据来源与区域间投入产出表编制说明
3.1. 数据来源
由于数据的可得性和投入产出表的特殊性,本文依照黄庆华(2021)的观点,近似认为成渝地区包含四川省和重庆市,并采用四川省和重庆市的投入产出表数据,编制成渝地区区域间投入产出表 [5] 。主要使用2017年的数据,其中2017年川渝的42部门投入产出表主要来自《中国地区投入产出表2017》,编制两地投入产出表用到的行政区域间货运交流数据则来源于当年的《中国铁道年鉴》。
3.2. 区域间投入产出表编制说明
要进行区域间投入产出分析研究,需要进行区域间投入产出表的编制,采用MRIO模型。过程简要如下:
3.2.1. 区域间流量的估算和调整
首先采用里昂惕夫等主张的引力模型估算区域间商品流量,其次得出区域间贸易矩阵。
引力模型的计算公式为:
(14)
公式(14)中
是部门i从地区R到地区S的流出量;
是R地区部门i的总产出量;
是地区S对部门i的总需求量;
是所有地区部门i的总产出量;
为从地区R到地区S产品流动的摩擦系数。其中总产出量
、总需求量
和总产出量
可从投入产出表计算得出,摩擦系数
的计算则根据运输量分布系数来测算。
计算模型为:
(15)
式(15)中,
为从地区R到地区S产品的运输量,
为地区R产品总的发送量,
为地区S产品总的到达量,
为全部地区产品总的发送量。通过《中国交通年鉴2017》国家铁路行政区域间货物交流表数据计算 [6] 。
3.2.2. 系数矩阵的计算
区域间投入产出表中行向量关系可表示为:
(16)
其中,C为区域间贸易系数矩阵,A为所有区域的直接消耗系数矩阵,X为总产出,F为各区域的最终需求,E、M分别为各区域的出口和进口向量,E-M则为各区域的净出口向量。
其中总产出X、区域最终需求F、区域出口E和区域进口M向量都在区域间投入产出表可以直接观察和得到,而区域间贸易系数矩阵C和直接消耗系数矩阵A需通过计算得出。
直接消耗系数各元素aij构成直接消耗系数矩阵,计算公式如下:
(17)
贸易系数矩阵由
构成,计算公式为:
(18)
公式(18)中的
则为根据前面所计算出的区域间贸易流量。
3.2.3. 区域间投入产出表的编制
基于以上公式进行计算,得出各矩阵中的元素,分别对应并进行排列,再加上出口和进口,最后就可根据区域间投入产出表的行列平衡关系进行编制,得到初步的成渝间区域投入产出表。
4. 实证分析
4.1. 成渝乘数、溢出和反馈效应汇总分析
首先对成渝两地的产业部门进行汇总计算和分析,进行后向联系测度,结果如表1所示。

Table 1. Summary of Chengdu-Chongqing multiplier effect, spillover effect and feedback effect
表1. 成渝乘数效应、溢出效应、反馈效应汇总
表1给出了成渝两地42个产业部门区域内乘数效应、区域间溢出效应、区域间反馈效应的汇总数据以及平均值。具体来说,重庆市区域内乘数效应测度为113.2374,体现出重庆市内产业部门变动对自身产出的影响,具体为当重庆市内的各产业部门同时增加1亿元的最终使用时,重庆市总产出将通过重庆市内部各产业间的相互联系增加113.2374亿元;区域间溢出效应测度为1.2996,体现出四川省产业部门变动对重庆市产出的影响程度,具体为当四川省各产业部门同时增加1亿元的最终使用时,重庆市总产值将通过四川省与重庆市的产业关联带动从而增加1.2996亿元 [7] 。区域间反馈效应测度为0.0146,体现出重庆市通过对四川省的影响反过来对自身产值的影响程度,具体为当重庆市的各产业部门同时增加1亿元的最终使用时,其自身将通过其与四川省间的产业联系带动自身总产出增加0.0146亿元 [4] 。四川省的分析则类似。
从区域内乘数效应来看,四川省的区域内乘数效应为116.2588明显高于重庆市的乘数效应113.2374,具体测度高于重庆市2.668%,当四川省内和重庆市内各部门同时增加1亿元时,四川省总产出增长将高于重庆市增长3.0214亿元,表明四川省区域内各产业间的联系强度明显高于重庆市,带来的经济效益也大于重庆市。
而从区域间溢出效应和区域间反馈效应来看,四川省的区域间溢出效应和反馈效应分别为0.754和0.0094,明显低于重庆市的溢出效应1.2996和反馈效应0.0146,分别低72.36%和55.32%,表明四川省通过两地之间的产业关联无论是给重庆市还是给自身带来的总产值增加 [7] ,都要比重庆市给四川省带来的增加少,从中可看出四川省的区域间产业联系强度和反馈和重庆市仍存在不少差距。
4.2. 成渝间各产业乘数、溢出和反馈效应比较研究
上面对四川省和重庆市各产业部门联系强度,以及给自身和对方在经济方面的带动和影响作用进行总的分析后,接下来则分别对各效应进行更为详细的分析,考察成渝间产业间的关联和产业结构的变化,探讨合适的产业配套模式和相应的产业经济政策。
4.2.1. 区域内乘数效应
表2为四川省和重庆市42产业部门的区域内乘数效应后向联系测度,衡量了该产业与区域内其他产业的联系强度。其中各项数字表示此产业部门受区域内其他产业部门影响的程度。具体来说,重庆市的农林牧渔产品和服务对应的数字为1.707,表示当重庆市内各产业部门同时增加1亿元最终使用时,重庆市的农林牧渔产品和服务产业部门将通过各产业部门的内部联系增加1.707亿元。其他产业部门则类似。

Table 2. Measurement of multiplier effect in 42 industrial regions of Sichuan province and Chongqing city
表2. 四川省和重庆市42产业区域内乘数效应测度
更为直观的,将表1中的成渝两地产业部门相关数据反映到图上,则将能更为明显地观察和比较成渝两地各产业部门联系强度,具体如图1所示。从图1可以看出,四川省区域内产业联系强度前五是金属制品、机械和设备修理服务,通信设备、计算机和其他电子设备,电气机械和器材,交通运输设备和通用设备;而重庆市为通信设备、计算机和其他电子设备,电气机械和器材,金属冶炼和压延加工品,仪器仪表以及建筑。一方面说明四川省和重庆市都存在各自的优势产业,四川省优势产业为金属制品、机械和设备修理服务,交通运输设备和通用设备,重庆市优势产业为金属冶炼和压延加工品,仪表仪器以及建筑 [7] 。另一方面两地区也存在相似的优势产业,例如通信设备、计算机和其他电子设备,电气机械和器材等,说明成渝两地区在许多产业上存在同质竞争。
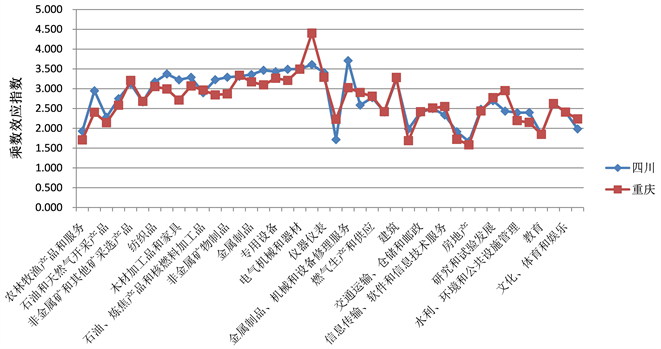
Figure 1. Multiplier effect of 42 industrial sectors in Sichuan and Chongqing
图1. 川渝42产业部门乘数效应
4.2.2. 区域间溢出效应
对四川省和重庆市各产业部门区域间溢出效应进行后向联系测度,具体如表3所示,衡量了本区域与另一区域产业的联系强度,体现出本区域产业部门受另一区域对应产业部门的影响程度。具体来说,重庆市的煤炭采选产品为9.229 × 10−3,表示当四川省各产业部门同时增加1亿元的最终使用时,重庆市的煤炭采选产品将由于与四川省煤炭采选产品的联系增加92.29万元。

Table 3. Measurement of inter-regional spillover effects of 42 industries in Sichuan and Chongqing
表3. 四川省和重庆市42产业区域间溢出效应测度
同样的,将表3中的结果反映到图中,得到图2。由表3及图2可看出,四川省各产业与重庆市各产业联系强度较强的有水的生产和供应,交通运输设备,通信设备、计算机和其他电子设备,非金属矿物制品,木材加工品和家具等;而重庆市与四川省各产业联系较强的为水的生产和供应,交通运输设备,食品和烟草,金属冶炼和压延加工品以及非金属矿物制品。从中可以看出,水的生产和供应,交通运输设备,非金属矿物制品等产业是川渝各产业联系较强的 [7] ,而根据黄庆华等(2021)根据赫希曼准则对川渝间核心关联产业的分析,包括造纸印刷和文教体育用品,化学产品,金属冶炼和压延加工品,通用设备、专用设备,通信设备、计算机和其它电子设备等也与川渝间联系较强产业类似 [5] 。一般区域内的优势产业对区域间经济的带动作用也会起到重要作用 [8] ,以重庆市为例,同样根据黄庆华等(2021)的分析,重庆市的主导产业包括造纸印刷和文教体育用品,石油、炼焦产品和核燃料加工品,化学产品,金属冶炼和压延加工品,通信设备、计算机和其它电子设备,电力、热力的生产和供应等,这些产业部门在上面的分析中在带动四川省经济增长也发挥了重要作用,而四川省内的主导产业虽多,但在拉动重庆市经济增长上发挥作用的产业相对较少,说明四川省对重庆市的经济拉动作用不如重庆市对四川省的经济带动程度。
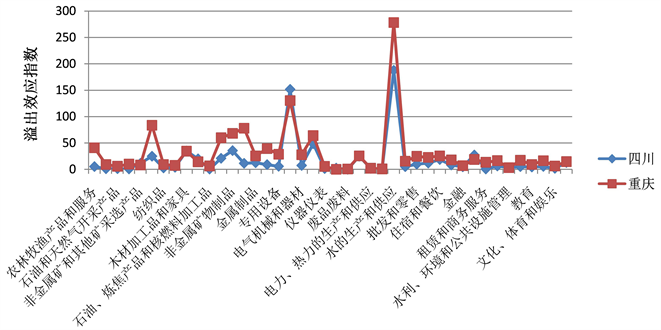
Figure 2. Spillover effects of 42 industrial sectors in Sichuan and Chongqing
图2. 川渝42产业部门溢出效应
4.2.3. 区域间反馈效应
对四川省和重庆市产业区域间反馈效应进行后向联系测度,具体如表4所示,与溢出效应类似,但体现出的是本区域产业部门对另一区域产业部门造成影响反过来对本区域对应产业部门的影响程度。具体来说,以重庆市的石油和天然气开采产品为0.051 × 10−3,表示当重庆市各产业部门同时增加1亿元最终使用时,通过对四川省经济增长的拉动,反馈到重庆市的石油和天然气开采产品总产值增加0.51万元。

Table 4. Linkage measure of inter-regional feedback effect of 42 industries in Sichuan province and Chongqing city
表4. 四川省和重庆市42产业区域间反馈效应联系测度
同样将表4的结果制成图形得到图3,结合图表可以观察出,四川省各产业对重庆市各产业反馈效应强度靠前的有交通运输设备,水的生产和供应,通信设备、计算机和其他电子设备,木材加工品和家具,食品和烟草等;而重庆市与四川省各产业反馈效应较强的有水的生产和供应,交通运输设备,非金属矿物制品,通信设备、计算机和其他电子设备,木材加工品和家具 [7] 。首先可以观察出溢出效应较强的产业和反馈效应基本类似,区域间溢出效应的变化方向和反馈效应也基本相同,变化幅度则相对更大,说明溢出效应和反馈效应一样都是反映产业的联系强度,一个反馈到自身,另一个反馈到其他区域;其次可以更为明显地发现重庆市各产业的溢出效应基本都要大于四川省各产业的溢出效应,与反馈效应类似的同时,也与上面分析的结果相一致,说明重庆市通过与四川省的联系无论是对四川省还是对自身的经济拉动作用都比四川省对重庆市的作用要大。
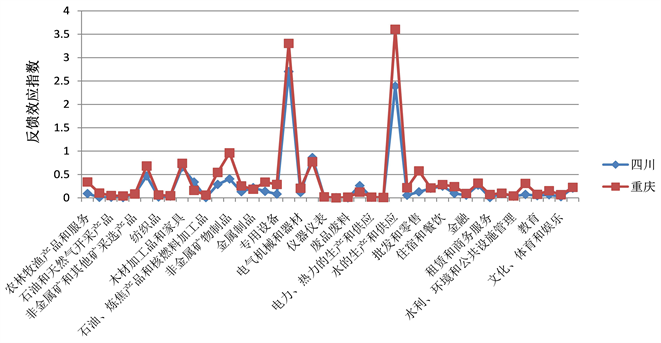
Figure 3. Feedback effect of 42 industrial sectors in Sichuan and Chongqing
图3. 川渝42产业部门反馈效应
5. 结论和政策建议
本文参照其他区域的投入产出分析 [9] ,采取传统的两区域投入产出模型,利用川渝两地2017年42部门投入产出表的数据,编制川渝两地区域投入产出表,通过投入产出分析方法分别对其进行区域内乘数效应、区域间溢出效应和区域间反馈效应进行分析,以研究两地间的经济发展规律,探讨成渝地区双城经济圈建设存在的问题。可以发现,随着两地经济的迅速增长,经济规模的扩大,两地间产业经济技术联系的增强,有形成统一市场和经济发展区域的需要和趋势,但两地由于地域和资源等各方面原因,不可避免的存在产业同质化竞争和市场分割等问题,致使两地间经济发展中所带来的整体规模和联系强度还较小。根据以上研究结论提出以下政策建议:
第一,发展优势产业,避免同质竞争。根据川渝两地产业乘数效应的分析,两地存在各自的优势产业,对区域内其他产业的发展具有重要的拉动作用,同时相似的优势产业也会出现同质竞争的现象,因此两地既要大力发展各自优势产业,如四川省内的金属制品、机械和设备修理服务,交通运输设备和通用设备以及重庆市内的金属冶炼和压延加工品,仪器仪表以及建筑产业,同时避免通信设备、计算机和其他电子设备,电气机械和器材等产业的同质竞争现象,权衡利弊,做好设计,实现两地的合理分工和资源的科学分配,从而将同质竞争的劣势转换为协同发展的优势。
第二,完善核心产业链配套,加强产业联系。根据川渝两地产业溢出效应和反馈效应的分析,两地间联系较强的相关产业不仅对其他区域的产业有拉动作用,反过来也会影响区域内产业的发展,如水的生产和供应、交通运输设备等产业,同时也与川渝间核心关联产业联系,因此整合利用各自资源发挥优势的同时,需加强合作交流,协同打造产业配套体系,促进产业融合发展,在联系较强的产业上形成完整可靠的区域产业链,根据不同区域的资源和技术条件,实现两地同一产业链的合理分工,延长和优化产业链。
第三,推动市场一体化建设,强化合作协同机制。根据以上效应的分析,虽然两地存在各自的优势产业与核心关联产业,并对区域间经济的发展起到带动作用,但川渝两地各自的拉动作用并不对等,重庆市对四川省在经济增长上的拉动作用明显大于四川省对重庆市的拉动作用,因此应加快推进统一大市场的形成,促进包括劳动力、技术创新、资金等在内的生产要素一体化,完善统筹协调机制,进一步强化地区间政策协同合作,减少市场准入门槛和不合理规定,推动政策一体化,增强经济活力,为打造市场一体化提供制度保障。