求解一维Allen-Cahn方程的保能量耗散Du Fort-Frankel格式

Energy Dissipation Du Fort-Frankel Scheme for 1D Allen-Cahn Equation

摘要: Allen-Cahn方程的保结构算法常常是全隐线性格式或全隐非线性格式。为提高计算效率，本文提出一类显式Du Fort-Frankel格式，所得数值解保持能量耗散定律。最后，数值结果验证了格式的有效性和保能量耗散性，同时在空间网格为h，时间步长τ = h²的情况下，得到数值解具有二阶的收敛精度。

Abstract: The structure-preserving algorithms for the Allen-Cahn equation are often fully implicit linear schemes or fully implicit nonlinear schemes. To improve computational efficiency, a class of explicit Du Fort-Frankel (DFF) schemes, whose numerical solutions inherit the energy dissipation law is proposed in this study. Finally, numerical results verify the validity and energy dissipation of the scheme. At the same time, under the condition of space grid h and time step τ = h², the numerical solutions converge to exact solution with an order of O(h²).

1. 引言

非线性抛物方程是一类重要的偏微分方程，来源于自然界中广泛存在的非线性现象。相变理论、渗透理论、图像处理和生物化学理论等领域中的许多问题都可以用这种方程来描述。Allen-Cahn方程是一类重要的二阶非线性抛物方程，该方程描述了形成界面和相互作用的过程。最早由Allen和Cahn [1] 提出，用于刻画二元合金在固定温度下相分离的过程。在过去的几十年中，Allen-Cahn方程及其各种修正形式广泛应用于科学和工程领域，如材料科学中的界面动力学 [2] [3] 、图像分割 [4] [5] 、相变 [6] [7] 和晶体生长 [8] [9] 。

本文将研究如下一维非线性Allen-Cahn方程的初边值问题(IBVP)

$\{\begin{array}{l}{u}_t-{\epsilon }^2\Delta u=f\left(u\right),x\in \text{Ω},t\in \left(0,T\right],\hfill \\ u\left(x,0\right)=u_0\left(x\right),x\in \text{<mover accent="true"> Ω <mo> ¯ </mo> </mover>},\hfill \\ u\left(x,t\right)=\phi \left(x,t\right),x\in \partial \text{Ω},t\in \left(0,T\right].\hfill \end{array}$ (1)

其中u表示二元合金中的一个金属部件的浓度， $\epsilon >0$ 表示接口的宽度，非线性项 $f\left(u\right)=-F^{\prime }\left(u\right)$ ， $F\left(u\right)=\left[b{\left(1-u^2\right)}^2\right]/4$ 。在文献 [10] 中，Du等利用谱方法解决非局部Allen-Cahn方程问题。Xiao等在文献 [11] 中分析了Allen-Cahn方程有限元方法的稳定性。Zhai等在文献 [12] 中关于Allen-Cahn方程建立了线性化高阶紧致差分方法，并采用交替方向隐格式减少计算量。Strachota等在文献 [13] 中利用有限体积方法求解Allen-Cahn方程并给出误差估计。另外，还可以利用重心插值配点法 [14] 和配点法 [15] 求解Allen-Cahn方程。但传统的数值方法在处理Allen-Cahn方程时常常面临保结构性的问题，众所周知，它的精确解具有能量耗散性，即：

当 $\phi \left(x,t\right)=0$ ， $\left(\left(x,t\right)\in \partial \text{Ω}\times \left[0,T\right]\right)$ 时，定义能量 $E\left(t\right)$ 和 $F\left(t\right)$ 如下

$E\left(t\right)=\frac{1}{2}{\displaystyle {\int }_{\text{Ω}}{\left|\nabla u\right|}^2+2F\left(u\right)\text{d}x\text{d}y}+c,$ (2)

$F\left(t\right)={\Vert u_t\Vert }^2+\frac{\text{d}}{\text{d}t}E\left(t\right)$ (3)

则有 $F\left(t\right)=0$ 和当 $t\le t^{\prime }$ 时有 $E\left(t^{\prime }\right)\le E\left(t\right)$ ，c为任意常数。

这个性质在研究Allen-Cahn方程的解的稳定性中很重要，并且能否在离散水平上继承这个性质是数值模拟中的一个重要问题。由于方程中存在梯度平方的项，传统的数值算法可能会出现数值耗散或者数值剧烈震荡的现象，从而导致数值解的不稳定性和不准确性。保结构数值算法在长时间数值模拟，以及提供高分辨率的数值解方面有显著优势。令人高兴的是，许多学者提出了各种各样的保结构算法。例如，文献 [16] 提出了Allen-Cahn方程的保最大值原理和能量耗散性的一阶线性隐显格式。文献 [17] 讨论了广义Allen-Cahn方程保最大值原理的一阶线性隐显格式。 [18] [19] [20] 中讨论了Allen-Cahn方程无条件能量稳定的有限差分法和有限元法。文献 [21] [22] [23] [24] [25] 对Allen-Cahn方程设计了一系列既保最大值原理又无条件能量稳定的差分法。大量的数值结果表明，尽可能继承原方程的性质可以产生更可靠的数值解，并有效地避免非物理振荡。

可以看出，Allen-Cahn方程的保结构算法常常是全隐线性格式，或者全隐非线性格式。它们计算复杂，耗时多。在文献 [26] 中，林研究了此方程组的显式保结构Du Fort-Frankel差分格式。陈等在文献 [27] 中提出一类非线性延迟波动方程的无条件稳定Du Fort-Frankel差分格式。张在文献 [28] 中建立了一维非线性耦合波动方程组的Du Fort-Frankel格式。王等在文献 [29] 中建立了CNLS方程组的显式保结构Du Fort-Frankel差分格式。受到抛物方程的DFF差分法和文献工作的启发，本文运用Du Fort-Frankel格式，对IBVP(1)构造了一类显式保能量耗散差分格式。该算法对网格条件并不苛刻且计算效率高，能够有效地保持离散能量的耗散性。本文我们将对算法进行详细地理论分析，并通过数值实验验证其可靠性。

本文的其余部分组织如下，在第二节中给出符号说明。第三节给出了保能量耗散Du Fort-Frankel格式的构造过程。第四节讨论了该格式的离散能量稳定性。第五节利用数值算例验证理论分析的准确性。第六节给出结论与展望。

2. 符号说明

取时间步长 $\tau =T/N\left(N\in Z^{+}\right)$ ，记 $t_k=k\tau$ ， $k=0,1,2,\cdots ,N$ 。对区域 ${\text{<mover accent="true"> Ω <mo> ¯ </mo> </mover>}}_{\tau }$ 进行剖分 ${\text{<mover accent="true"> Ω <mo> ¯ </mo> </mover>}}_{\tau }=\left\{t_k|0\le k\le N\right\}$ ，且记 ${\text{Ω}}_{\tau }=\left\{t_k|0\le k\le N-1\right\}$ 。在时间区域 ${\text{Ω}}_{\tau }$ 上，差分算子定义如下：

${\delta }_t{v}^{k+\frac{1}{2}}=\frac{v^k-v^{k-1}}{\tau },{\delta }_{\hat{t}}{v}^k=\frac{v^{k+1}-v^{k-1}}{2\tau }=\frac{{\delta }_t{v}^{k+\frac{1}{2}}+{\delta }_t{v}^{k-\frac{1}{2}}}{2},{\delta }_t^2{v}^k=\frac{{\delta }_t{v}^{k+\frac{1}{2}}-{\delta }_t{v}^{k-\frac{1}{2}}}{\tau }=\frac{v^{k+1}-2v^k+v^{k-1}}{{\tau }^2}$

另外取空间步长 $h_x=\left(b-a\right)/M\left(M\in Z^{+}\right)$ ，记 $x_i=a+i{h}_x$ ， $i=0,1,2,\cdots ,M$ 。对区域 ${\text{Ω}}_h$ 进行剖分 ${\text{Ω}}_h=\left\{x_i|1\le i\le M\right\}$ ，并且 $\partial {\text{Ω}}_h=\left\{x_i|i=0或M\right\}$ ，记 ${\text{<mover accent="true"> Ω <mo> ¯ </mo> </mover>}}_h={\text{Ω}}_h\cup \partial {\text{Ω}}_h$ 。令 $S_h=\left\{v|v=\left\{v_i|x_i\in {\text{<mover accent="true"> Ω <mo> ¯ </mo> </mover>}}_h\right\}\right\}$ ， $S_h^0=\left\{v|v\in S且当x_i\in \partial {\text{Ω}}_h时有v_i=0\right\}$ 为网格函数。在区域 ${\text{Ω}}_h$ 上， $\forall v\in S_h$ 时，空间区域上的差分算子定义如下：

${\delta }_x{v}_{i+\frac{1}{2}}=\frac{v_{i+1}-v_i}{h},{\Delta }_h{v}_i={\delta }_x^2{v}_i=\frac{v_{i+1}-2v_i+v_{i-1}}{h^2}$

当 $\forall U,V\in S_h^0$ ，内积和范数定义如下：

$\begin{array}{l}\langle U,V\rangle =h{\displaystyle {\sum }_{i=1}^{M-1}{U}_i{V}_i},\langle {\delta }_{x}U,{\delta }_{x}V\rangle =h{\displaystyle {\sum }_{i=1}^{M-1}{\delta }_x{U}_{i-\frac{1}{2}}{\delta }_x{V}_{i-\frac{1}{2}}},{\Vert V\Vert }^2=\langle V,V\rangle ,\text{1}\\ {\left|V\right|}_{H^1}^2={\Vert {\delta }_{x}V\Vert }^2=\langle {\delta }_{x}V,{\delta }_{x}V\rangle ,{\Vert V\Vert }_{H^1}^2={\Vert V\Vert }^2+{\left|V\right|}_{H^1}^2,{\Vert V\Vert }_{\infty }=\max \left|V_i^k\right|\end{array}$

为了方便起见，下面定义一些集合：

$\Gamma =\left\{k|1\le k\le N-1\right\},\partial \Gamma =\left\{k|k=0或N\right\},\Upsilon =\left\{i|1\le i\le M-1\right\},\partial \Upsilon =\left\{i|i=0或M\right\}$

3. 差分格式的建立

本节讨论保能量耗散Du Fort-Frankel格式的建立。记 $u_i^k$ ， $U_i^k$ 分别表示保能量耗散Du Fort-Frankel格式在 $\left(x_i,t_k\right)$ 处的精确解和数值解。

在结点 $\left(x_i,t_k\right)$ 处考虑方程(1)有

$u_t\left(x_i,t_k\right)=\alpha \Delta u\left(x_i,t_k\right)-F^{\prime }\left[u\left(x_i,t_k\right)\right]$ (4)

其中 $\alpha >0$ ，利用Du Fort-Frankel有限差分法， ${\delta }_{\hat{t}}{u}_i^k$ 和 $\frac{F\left(u_i^{k+1}\right)-F\left(u_i^{k-1}\right)}{u_i^{k+1}-u_i^{k-1}}$ 分别离散 $\Delta u\left(x_i,t_k\right)$ ， $u_t\left(x_i,t_k\right)$ 和 $F^{\prime }\left[u\left(x_i,t_k\right)\right]$ ，并且在等式左端加上稳定项 ${\beta }^2{\tau }^2{\delta }_t^2{u}_j^k$ 可得

${\delta }_{\hat{t}}{u}_i^k+{\beta }^2{\tau }^2{\delta }_t^2{u}_i^k+\alpha {\left(\frac{\tau }{h}\right)}^2{\delta }_t^2{u}_i^k=\alpha {\delta }_x^2{u}_i^k-\frac{F\left(u_i^{k+1}\right)-F\left(u_i^{k-1}\right)}{u_i^{k+1}-u_i^{k-1}}+R_i^k\text{,}i\in \text{Υ,}k\in \text{Γ}\text{.}$ (5)

其中

$\begin{array}{c}{R}_i^k=\frac{{\tau }^2}{6}\frac{{\partial }^{3}u}{\partial t^3}\left(x_i,{\zeta }_k\right)+\alpha \left[\frac{{\tau }^2}{h^2}\frac{{\partial }^{2}u}{\partial t^2}\left(x_i,{\xi }_k\right)-\frac{h^2}{12}\frac{{\partial }^{4}u}{\partial x^4}\left({\varsigma }_i,t_k\right)\right]\\ +{\beta }^2{\tau }^2\frac{{\partial }^{2}u}{\partial t^2}\left(x_i,{\varrho }_k\right)+\tau b\left\{\frac{{\left(\frac{\partial u}{\partial t}\left(x_i,{\eta }_{k_1}\right)\right)}^2}{2\frac{\partial u}{\partial t}\left(x_i,{\eta }_{k_2}\right)}\left[3{\left(u\left(x_i,{\eta }_{k_3}\right)\right)}^2-1\right]+\frac{{\left(\frac{\partial u}{\partial t}\left(x_i,{\eta }_{k_4}\right)\right)}^2}{2\frac{\partial u}{\partial t}\left(x_i,{\eta }_{k_2}\right)}\left[3{\left(u\left(x_i,{\eta }_{k_5}\right)\right)}^2-1\right]\right\}\end{array}$ (6)

$x_{i-1}\le {\varsigma }_i\le x_{i+1}$ , $t_k\le {\eta }_{k_1},{\eta }_{k_3}\le t_{k+1}$ , $t_{k-1}\le {\eta }_{k_4},{\eta }_{k_5}\le t_k$ , $t_{k-1}\le {\zeta }_k,{\xi }_k,{\varrho }_k,{\eta }_{k_2}\le t_{k+1}$ .

由于差分格式(9)~(12)是三层格式，已知第0层的数值解，为了启动计算，第一层的数值解采用以下差分格式 [30] 计算

${\delta }_t{u}_i^{\frac{1}{2}}-\alpha {\delta }_x^2{u}_i^0-b{u}_i^0+b{u}_i^1{\left(u_i^0\right)}^2=R_i^0,i\in \Upsilon$ .(7)

求出第一层的数值解，其中

$R_i^0=\frac{\tau }{2}\frac{{\partial }^{2}u}{\partial t^2}\left(x_i,{\zeta }_0\right)+b\tau {\left[u\left(x_i,t_0\right)\right]}^2\frac{\partial u}{\partial t}\left(x_i,{\xi }_0\right)-\alpha \frac{h^2}{12}\frac{{\partial }^{4}u}{\partial x^4}\left({\varsigma }_i,t_k\right),t_0\le {\zeta }_0,{\xi }_0\le t_1,x_{i-1}\le {\varsigma }_i\le x_{i+1}$ (8)

在方程(5)和(7)中略去小量项 $R_i^k\left(k=0,1,2,\cdots ,N-1\right)$ ，用数值解 $U_i^k$ 代替精确解 $u_i^k$ ，得到如下保能量耗散Du Fort-Frankel格式

${\delta }_{\hat{t}}{U}_i^k+{\beta }^2{\tau }^2{\delta }_t^2{U}_i^k+\alpha {\left(\frac{\tau }{h}\right)}^2{\delta }_t^2{U}_i^k=\alpha {\delta }_x^2{U}_i^k-\frac{F\left(U_i^{k+1}\right)-F\left(U_i^{k-1}\right)}{U_i^{k+1}-U_i^{k-1}},i\in \Upsilon ,k\in \text{Γ}$ , (9)

${\delta }_t{U}_i^{\frac{1}{2}}=\alpha {\delta }_x^2{U}_i^0+b{U}_i^0-b{U}_i^1{\left(U_i^0\right)}^2,i\in \Upsilon$ (10)

$U_i^0=u\left(x_i,t_0\right),i\in \Upsilon \cup \partial \Upsilon$ ,(11)

$U_i^k=\phi \left(x_i,t_k\right),i\in \partial \Upsilon ,k\in \text{Γ}.$ (12)

4. 离散能量的耗散性

引理1 (cf. [31] )对于任意网格函数 $U\in S_h^0$ ，有以下结论成立。

$h^2\Vert {\delta }_x{V}^2\Vert \le 4{\Vert V\Vert }^2$

引理2 对于任意网格函数 $U\in S_h^0$ ，有以下结论成立。

$\langle {\delta }_x{U}_i^{k+1},{\delta }_x{U}_i^k\rangle \ge {\Vert {\delta }_x{U}^{k+\frac{1}{2}}\Vert }^2-{\left(\frac{\tau }{h}\right)}^2{\Vert {\delta }_t{U}^{k+\frac{1}{2}}\Vert }^2$

证利用等式 $ab=\frac{{\left(a+b\right)}^2-{\left(a-b\right)}^2}{4}$ 以及引理1可得

$\langle {\delta }_x{U}_i^{k+1},{\delta }_x{U}_i^k\rangle ={\Vert {\delta }_x{U}^{k+\frac{1}{2}}\Vert }^2-\frac{{\tau }^2}{4h^2}{h}^2{\left|{\delta }_t{U}^{k+\frac{1}{2}}\right|}_{H^1}^2\ge {\Vert {\delta }_x{U}^{k+\frac{1}{2}}\Vert }^2-{\left(\frac{\tau }{h}\right)}^2{\Vert {\delta }_t{U}^{k+\frac{1}{2}}\Vert }^2$ . (13)

定理1 设 $\left\{U_i^k|i\in \Upsilon \cup ,\partial \Upsilon ,0\le k\le N\right\}$ 是差分格式(9)~(12)的解。离散能量 $E^k$ 和 $F^k$ 分别定义为

$E^k=\frac{\left(\alpha +{\beta }^2{h}^2\right){\tau }^2}{2h^2}{\Vert {\delta }_t{U}^{k+\frac{1}{2}}\Vert }^2+\frac{\alpha }{2}\langle {\delta }_x{U}_i^{k+1},{\delta }_x{U}_i^k\rangle +\frac{h}{2}{\displaystyle {\sum }_{i=1}^{M-1}\left[F\left(U_i^{k+1}\right)+F\left(U_i^k\right)\right]}$ , (14)

$F^k={\Vert {\delta }_{\hat{t}}{U}^k\Vert }^2+{\delta }_t{E}^{k-\frac{1}{2}}$ , (15)

则有 $F^k=0\left(k=1,2,\cdots ,N-1\right)$ 和 $E^k\le E^{k-1},k=1,2,\cdots ,N-1$ ，并且有 $E^k\ge 0,k=1,2,\cdots ,N-1$ 。

证首先将(9)两边同时与 ${\delta }_{\hat{t}}{U}_i^k$ 作内积，并运用格林公式可得

$\begin{array}{c}{\Vert {\delta }_{\hat{t}}{U}^k\Vert }^2=\langle \alpha {\delta }_x^2{U}_i^k-\left(\alpha \frac{{\tau }^2}{h^2}+{\beta }^2{\tau }^2\right){\delta }_t^2{U}_i^k,{\delta }_{\hat{t}}{U}_i^k\rangle -\langle \frac{F\left(U_i^{k+1}\right)-F\left(U_i^{k-1}\right)}{U_i^{k+1}-U_i^{k-1}},\frac{U_i^{k+1}-U_i^{k-1}}{2\tau }\rangle \\ =-\frac{\alpha }{2\tau }\left[\langle {\delta }_x{U}_i^{k+1},{\delta }_x{U}_i^k\rangle -\langle {\delta }_x{U}_i^k,{\delta }_x{U}_i^{k-1}\rangle \right]-\frac{\left(\alpha +{\beta }^2{h}^2\right){\tau }^2}{2h^2}\left({\Vert {\delta }_t{U}^{k+\frac{1}{2}}\Vert }^2-{\Vert {\delta }_t{U}^{k-\frac{1}{2}}\Vert }^2\right)\\ -\frac{h}{2\tau }{\displaystyle \underset{i=1}{\overset{M-1}{\sum }}\left[F\left(U_i^{k+1}\right)+F\left(U_i^k\right)-F\left(U_i^k\right)-F\left(U_i^{k-1}\right)\right]}\end{array}$

根据(14)，上式可等价写为

$F^k={\Vert {\delta }_{\hat{t}}{U}^k\Vert }^2+{\delta }_t{E}^{k-\frac{1}{2}}=0,k=1,2,\cdots ,N-1$

故有 $E^k\le E^{k-1}\left(k=1,2,\cdots ,N-1\right)$ 成立。

另外，由引理2有

$\begin{array}{c}{E}^k=\frac{\left(\alpha +{\beta }^2{h}^2\right){\tau }^2}{2h^2}{\Vert {\delta }_t{U}^{k+\frac{1}{2}}\Vert }^2+\frac{\alpha }{2}\langle {\delta }_x{U}_i^{k+1},{\delta }_x{U}_i^k\rangle +\frac{h}{2}{\displaystyle \underset{i=1}{\overset{M-1}{\sum }}\left[F\left(U_i^{k+1}\right)+F\left(U_i^k\right)\right]}\\ \ge \frac{{\beta }^2{\tau }^2}{2}{\Vert {\delta }_t{U}^{k+\frac{1}{2}}\Vert }^2+\frac{\alpha }{2}{\Vert {\delta }_x{U}^{k+\frac{1}{2}}\Vert }^2+\frac{h}{2}{\displaystyle \underset{i=1}{\overset{M-1}{\sum }}\left[F\left(U_i^{k+1}\right)+F\left(U_i^k\right)\right]}\ge 0\end{array}$

证毕。

5. 数值实验

本节将给出求解一维Allen-Cahn方程的两个数值算例，以证实理论结果的正确性和算法的高效性。为了验证算法的精度，在 $t_k$ 处数值解在不同范数下的误差定义如下： $L^{\infty }$ 范数误差为 $ME\left(h,\tau \right)={\Vert u^k-U^k\Vert }_{\infty }$ ， $L^2$ 范数误差为 $LE\left(h,\tau \right)=\Vert u^k-U^k\Vert$ ， $H^1$ 范数误差为 $HE\left(h,\tau \right)={\Vert u^k-U^k\Vert }_{H^1}$ 。其对应的收敛阶定义为： $M{R}_1={\log }_2\left[ME\left(2h_x,2\tau \right)/ME\left(h_x,\tau \right)\right]$ ， $L{R}_1={\log }_2\left[LE\left(2h_x,2\tau \right)/LE\left(h_x,\tau \right)\right]$ ， $H{R}_1={\log }_2\left[HE\left(2h_x,2\tau \right)/HE\left(h_x,\tau \right)\right]$ 。

算例1 [32] 考虑如下一维Allen-Cahn方程的IBVP

$\frac{\partial u}{\partial t}=\alpha \frac{{\partial }^{2}u}{\partial x^2}+bu\left(1-u^p\right)$ , $-L<x<L$ , $0<t\le T$ ,

$u\left(x,0\right)=\frac{1}{2}\tanh \left[-\frac{p}{2\sqrt{2p+4}}x\right]+\frac{1}{2}$ , $-L\le x\le L$ ,

$u\left(L,t\right)=\frac{1}{2}\tanh \left[-\frac{p}{2\sqrt{2p+4}}\left(L-\frac{p+4}{\sqrt{2p+4}}t\right)\right]+\frac{1}{2}$ , $0\le t\le T$ ,

$u\left(-L,t\right)=\frac{1}{2}\tanh \left[-\frac{p}{2\sqrt{2p+4}}\left(-L-\frac{p+4}{\sqrt{2p+4}}t\right)\right]+\frac{1}{2}$ , $0\le t\le T$ ,

当 $p=2$ 时，上述方程组为一维Allen-Cahn方程的IBVP，特别地，当 $\alpha =b=1$ 时该方程的精确解为

$u\left(x,t\right)=\frac{1}{2}\tanh \left[-\frac{p}{2\sqrt{2p+4}}\left(x-\frac{p+4}{\sqrt{2p+4}}t\right)\right]+\frac{1}{2}$

令 $\text{Ω}=\left[-5,5\right]$ ， $T=1$ ，以及参数 $\alpha =b=1$ 。图1展示了运用差分法(9)~(12)，在取参数 $\beta =3$ ，空间步长 $h=1/8$ ，时间步长 $\tau =1/64$ 和参数 $\beta =30$ ，空间步长 $h=1/16$ ，时间步长 $\tau =1/256$ 两种情况下求出的误差曲面图，由此可以看出数值解能够较好地逼近精确解。表1给出了取 $\beta =3$ 时，差分格式(9)~(12)在取不同网格步长时所得数值解 $u_i^k$ 的误差与收敛阶，表2给出了取 $\beta =30$ 时，差分格式(9)~(12)在取不同网格步长时所得数值解 $u_i^k$ 的误差与收敛阶，表明差分法(9)~(12)在最大范数意义下具有时间一阶空间二阶的收敛阶。验证了算法的高效性并且数值结果与理论结果相吻合。

Table 1. Numerical results at T = 1 obtained by our FDMs for example 1 with β = 3 (τ = h2)

表1. 取T = 1和β = 3时本文有限差分格式所获数值结果(τ = h²)

Table 2. Numerical results at T = 1 obtained by our FDMs for Example 1 with β = 30 (τ = h2)

表2. 取T = 1和β = 30时本文有限差分格式所获数值结果(τ = h²)

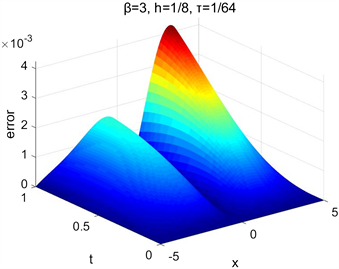
Figure 1. The surfaces of the error for different parameters β, h and τ

图1. 取不同β和步长时的误差曲面图

算例2 [24] 考虑如下一维Allen-Cahn方程的初值问题

$\{\begin{array}{ll}{u}_t=\alpha \Delta u+bu\left(1-u^2\right),\hfill & x\in \text{Ω},t\in \left(0,2\pi \right],\hfill \\ u\left(x,t\right)=0,\hfill & x\in \partial \text{Ω},t\in \left(0,2\pi \right],\hfill \\ u_0\left(x\right)=0.05\sin \left(x\right),\hfill & x=\left(0,2\pi \right).\hfill \end{array}$

在取空间步长为 $h=1/8$ ，时间步长为 $\tau =1/64$ 与参数 $\beta =3$ 情况下的数值求解，图2为 $b=1$ ， $\alpha$ 取不同值时离散能量 $E^k$ 和 $F^k$ 随时间的演化图，图3为 $\alpha =1$ ， $b$ 取不同值时离散能量 $E^k$ 和 $F^k$ 随时间的演化图。它们表明了该离散能量 $E^k$ 随时间的增加而减少，并且 $F^k\approx 0$ 。这些结果与理论结果相吻合。

Figure 2. Time evolutions of E^k, F^k for different parameters α

图2. 取不同α时的E^k，F^k随时间演化图

Figure 3. Time evolutions of E^k, F^k for different parameters b

图3. 取不同b时的E^k，F^k随时间演化图

6. 结论

本文针对一维Allen-Cahn方程构造了一类显式保能量耗散Du Fort-Frankel格式，并且分别从理论和实验两个方面证明了所得的离散能量满足能量耗散定律。数值算例验证了在 $\tau =h^2$ 的情况下时，所得数值解有 $O\left(h^2\right)$ 的收敛阶，在计算效率方面高于全隐保结构格式。另外，当T = 1000时，在扩散占优和反应占优的情况下所得数值解仍然满足能量耗散定律，可见，本文所建立的保结构算法具有长时间稳定性，高效性的优势。

尽管本文仅研究一维问题，事实上，本文的保结构方法可以很容易推广到高维问题的求解。

基金项目

江西省杰出青年基金(20212ACB211006)；江西省自然科学基金(20202BABL201005)；国家自然科学基金项目(No. 11861047)。