1. 引言
近年来,由于移动通信技术的快速发展,用户设备(User Equipment, UE)的数量显著增加。这一激增导致了许多新颖的普适应用的出现,例如虚拟现实、健康监测和实时互动游戏 [1] 。尽管近年来取得了一些进展,但用户终端的有限物理尺寸和电池容量意味着计算密集型应用需要更长的处理时间。这一限制导致目前移动终端的计算能力不足 [2] ,这对于移动设备实现这些应用程序构成了重大挑战。此外,随着物联网(Internet of Things, IoT)设备的年度增加,全球移动网络和云计算基础设施面临着相当大的困难。
为了解决上述挑战,移动边缘计算(Mobile Edge Computing, MEC)应运而生,并得到了众多研究人员的广泛研究 [3] 。MEC在移动网络的边缘部署服务器,靠近移动用户,为移动用户提供高效的IT服务环境和云计算能力 [4] 。然而,边缘计算服务器的固定部署限制了处理紧急情况的能力,特别是在无法建立无线网络的地区,如战区。此外,服务器部署的高成本阻碍了在需要大量基础设施的环境中进行实际部署 [5] 。因此,引入了一种利用灵活的无人机(Unmanned Aerial Vehicles, UAVs)支持的移动边缘计算系统。
然而,在当前阶段,将无人机视为边缘服务器与实际飞行环境之间仍存在差距。实际情况下,无人机操作的场景要复杂得多。现有的模拟和仿真环境往往无法完全复制真实飞行条件,导致一系列问题,如性能预测不准确、通信不稳定和感知与决策能力不足。因此,进一步研究和改进飞行环境模拟技术对于实现无人机作为边缘服务器部署,并使其与真实飞行条件更加接近至关重要。
因此,为了使模拟环境更接近无人机的真实飞行环境,本文提出了一种改进的场景,更有效地捕捉了真实环境的复杂性和变化性。
本文的主要贡献可以总结如下:
1) 本文提出了一个动态场景,更接近无人机的真实飞行环境,确保模拟环境更准确地捕捉真实环境的复杂性和多变性。
2) 我们本文将三个因素纳入奖励矩阵中:无人机飞行能量消耗,与静态和移动障碍物相关的风险,以及终端用户需求的动态变化。
3) 本文进行了大量实验,比较了不同算法在各种场景和不同数量的终端用户下的性能。结果表明,所提出的场景在进行相关研究时实现更接近真实环境的必要性。
本文的其余部分安排如下。第2节介绍了相关工作。第3节通过仿真验证了所提出模型的有效性,在第4节进行了总结。
2. 系统模型
在场景设置当中,场景包含处于起始位置的三架无人机,以及静态和移动的障碍物,还有终端用户和无人机飞行目标点的存在。在这个场景中,无人机充当边缘服务器,从起始点飞往目标终点。在此过程中,无人机为终端用户提供服务,并减少避免障碍物的风险。在起始点的无人机飞行过程中,地图上出现的其余无人机将充当移动障碍物,不断移动。同时,无人机共享终端信息和障碍物信息,终端用户的需求将在无人机达到其可服务范围之前开始自主处理。在这个过程中,终端用户的需求将作为无人机的奖励因素,而障碍物、飞行能耗作为成本因素。
令U表示所有无人机的集合,O表示所有障碍物的集合。为了在无人机飞行的每个阶段实现最优策略,每个无人机将充当代理者,不断从环境中学习。在每一步中,无人机根据周围环境选择规划策略,以实现最佳奖励。这些元素以奖励矩阵的形式反馈给移动的无人机。无人机根据生成的随机迭代成本矩阵G不断学习,选择从起始点到目标点的路径,同时为终端用户提供服务、避开障碍物,并实现高质量的服务。
2.1. 障碍物模型
在假设中,所有障碍物都符合高斯分布,但它们的风险暴露概率使用不同的方差
进行计算。我们将使用
表示地图上的坐标,我们将场景分为
的网格,坐标点代表的是网格中的每一个交叉点的坐标。对于地图中的独立障碍物,给出第i个障碍物的位置
,风险
[6] 表示在点
处来自
的风险,并可以定义为:
(1)
地图上从一个点到另一个点的风险暴露风险
由两点之间线性路径上任意点的积分风险表示。
(2)
对于第i个移动障碍物,其位置在随机方向和速度 [7] 下保持移动,其位置
为
(3)
其中,
表示随机方向
,范围为
。
表示随机角度,其范围值
,q表示随机距离,其值基于具体的实验设置确定,在实验中,随机移动的调整时间根据无人机每次移动一个网格单位的时间保持一致。
模型中符号说明如下表1。
2.2. 终端用户模型
对于终端用户,本文假设第j个终端用户具有初始需求
,等待无人机进行处理。假设无人机只能在一定的服务半径内满足需求,用
表示,
表示终端用户的位置,
表示可服务半径。由第k个无人机
服务的需求
可以随时间
变化表示为 [6] :
(4)
其中,
表示每个时间槽可以处理的需求数量。终端用户的剩余需求越大,无人机所需的服务时间就越长。
本文利用一种类似于Sigmoid函数的方法来增强强信号并减弱弱信号,描述实际需求与检测需求之间的相关性。该方法旨在提高系统的性能和稳定性。下面的S型需求检测函数
[8] 和 [9] 用于描述这种关系。
(5)
参数
控制需求曲线的斜率和中心位置,通过一个拐点
进行旋转。参数
控制需求曲线的
水平移动。为了计算服务质量并便于进行更好的实验比较,定义了具体的参数。服务质量被定义为: [6]
(6)
在无人机到达之前,终端用户会自行进行一部分处理,但由于其有限的自处理能力,需要无人机来协助处理未完成的需求。该模型的目的是优化无人机对终端用户需求的响应和处理效率,提高整个系统的性能和用户满意度。具体而言,可以通过马尔可夫随机矩阵的迭代计算 [10] ,模拟无人机在不同状态下的行为和决策,以优化其对终端用户需求的响应和处理效率。定义迭代矩阵A和初始成本矩阵B:
(7)
在每次无人机移动后,终端用户首次处理的未完成需求被表示为
(
),而后续迭代的乘积为
。经过多次迭代,未完成的需求将逐渐稳定下来。矩阵A中的每一列代表不同的需求进出比例。其中,a代表终端用户当前独立处理的需求比例,而
代表剩余的比例。b代表能够完全独立处理其需求的终端用户比例,而
代表由于意外情况而未满足的需求比例。因此,总未完成需求可以表示为
(8)
此外,引入了两个关键变量来描述无人机移动的时间和终端处理的频率,即step和t。其中,t代表完成一次固定移动所需的时间,而
代表t的倍数。因此,step代表终端处理的频率。
为了确保满足终端用户的需求,建议终端处理的频率应考虑无人机移动速度作为参考。这将防止终端用户处理过快导致需求迅速减少,从而最终提高整个系统的效率和稳定性。具体而言,在设计和实施无人机系统时应考虑因素
和t,以确保系统能在实际应用中实现最佳结果和性能。
2.3. 奖励矩阵
为了优化无人机的路径规划,本研究引入了一个奖励矩阵。该矩阵旨在测量地图上的任意点到另一点的奖励或惩罚,考虑了几个因素,如几何距离、动态终端需求、风险和无人机能量消耗。通过学习奖励矩阵,无人机可以确定最佳路径,以最小化能量消耗和风险,同时满足动态需求。本文拟采用一种路径规划算法,使无人机能够通过学习和调整奖励值来自主选择最佳路径。这种方法的目的是促进无人机的自主决策,从而提高系统性能和效率。
本文参考了文献 [6] 中的奖励矩阵模型。地图上点
和
之间的奖励矩阵定义如下:
(9)
矩阵行列数由定义地图网格N体现,其中奖励矩阵考虑了几个因素。首先,
表示点
和
之间的几何距离,这是一个基本的距离成本,也就是无人机的功耗。第二项表示从点
到
之间检测到的风险。最后,还考虑了在点
处检测到的需求量。奖励矩阵结合了这三个因素,指导无人机的路径规划决策。
2.4. 成本矩阵
在路径规划过程中,利用成本矩阵 来确定到目标点的初始最优路径。生成该矩阵涉及一个迭代过程,在多次迭代后最终收敛 [6] 。为每个无人机计算成本矩阵 的过程如下:
1) 初始化成本矩阵。将目标点赋值为0,将非目标点的元素赋值为无穷大。
2) 更新成本矩阵的过程如下:选择地图中的一个点,并根据其他点的赋值更新成本值(其中k为迭代次数)。
3) 重复步骤2),直到矩阵收敛到稳定状态。
(10)
在更新成本矩阵直到其收敛到最终稳定状态的过程中,生成了一个有序的点序列作为无人机的初始路径。在生成成本矩阵G之后,为每个无人机生成一个有序的点序列Path作为其初始路径。每个无人机根据其当前位置,不断将G中的最低成本点添加到其路径Path中。利用成本矩阵G,无人机计算下一个目标位置,直到所有飞机到达各自的目的地。
2.5. 路径规划
具体来说,每个无人机根据成本矩阵G生成自己的点序列作为初始路径。在成本矩阵G中,选择具有最低成本的点,并将其不断添加和更新到路径中。这个过程的描述如下: [11] 。
1) 将初始化为空。
2) 将G中的最小值
添加到Path中,并将
设置为无穷大。
3) 重复步骤2)直到达到目标点。
在这个过程中,每个无人机被视为一个智能体,每个无人机都拥有自己的记忆
和成本矩阵
。
负责存储环境的地图信息,而
则作为生成学习结果和选择无人机下一步动作的智能中枢。
在无人机移动的过程中,某些障碍物会发生位移。同时,终端用户将进行自处理。对于第i个无人机,如果它到达目标点,则停止其动作。如果任何其他无人机已到达其目的地,则该无人机从其记忆中删除相应的存在。在观测半径为R的圆形区域内,无人机扫描区域。当第i个无人机检测到障碍物时,它会更新其记忆中关于障碍物的信息,并与其他无人机共享这些信息,以协同规划下一步行动。每当存储在记忆中的环境发生变化时,权重矩阵和成本矩阵将相应更新,并重新计算
。如果没有变化发生,无人机将沿着现有路径
继续飞行,并且得到第i个无人机的新位置。
3. 仿真和讨论
本节首先讨论了无人机在复杂环境中的运动,并将其与在标准固定环境中的飞行进行了比较。此外,本文还比较了在相同复杂环境中,所提出的路径规划算法与经典的A*算法之间的适应能力差异。
在实验中,环境地图被定义为一个
(
)的网格,上下界限边界值定为1。在地图上,有三个无人机、十九个终端用户、十个障碍物和多个无人机共享的目标点。实验将模拟三个无人机从起点飞行到目标点的过程。在此过程中,无人机将选择合适的路径到达目标点,同时避免障碍物带来的风险,并为终端用户提供服务。三个无人机的路径将用不同颜色的线条表示。
在模拟过程中,根据参考表2初始化了参数,并根据具体的实验条件调整了参数值。

Table 2. Table of experimental parameters summary
表2. 实验参数表
3.1. 多无人机的路径规划
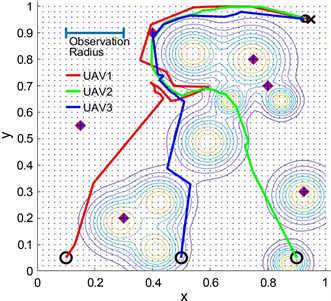
在图1中,整个地图以网格的形式呈现,被划分为一组网格。通过使用网格,可以将连续空间中的复杂问题转化为离散的基于网格的问题,有效地表示空间域内的位置和布局。此外,利用网格与常见的搜索算法兼容,便于与本研究提出的算法进行比较分析。通过将连续空间离散化为基于网格的表示,可以利用已建立的搜索算法,如A*算法 [6] ,高效地导航和探索离散的网格结构。这种兼容性使得提出的算法与现有方法之间可以进行有意义的比较,从而提供有效性和潜在优势方面的见解。
 (a) step = 5 (b) step = 30
(a) step = 5 (b) step = 30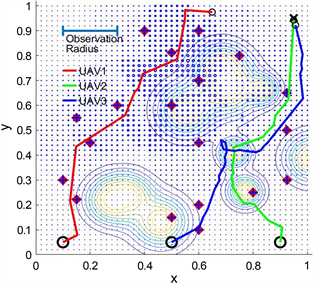
 (c) step = 180 (d) step = 195
(c) step = 180 (d) step = 195
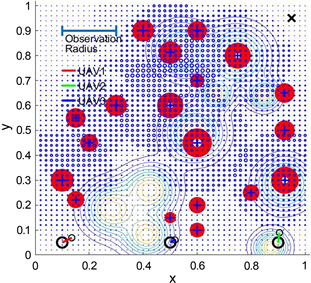
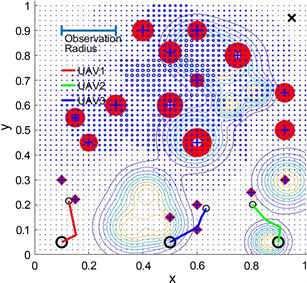
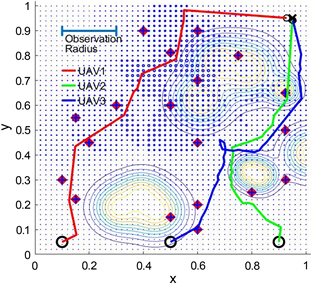
Figure 1. Simulation of UAV-MEC based on proposed path planning platform
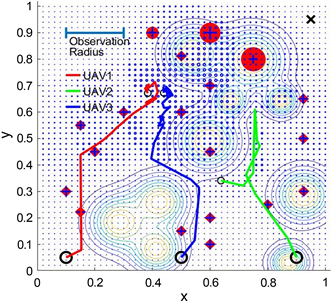
图1. 基于路径规划平台的无人机边缘计算系统仿真,环境:固定和移动障碍物,动态需求,考虑能量消耗
地图上的无人机、终端用户和障碍物将具有各自的坐标,代表它们的位置。在地图上,底部的三个黑色圆圈表示三个无人机,而中心带有蓝色十字的红色圆圈表示终端用户。围绕终端用户的较暗的点表示以终端用户为中心的无人机的操作范围。插图中形成形状的等高线表示障碍物的位置,等高线本身表示与障碍物相关联的风险范围。
通过图1,可以明显看出无人机在复杂环境中的导航面临更多的挑战和困难。这些挑战包括不断变化的障碍物位置和形状、动态的风险区域,以及不断减少的终端需求,需要无人机路径的适应性来满足不断变化的情况。由于复杂环境中各种因素的影响,无人机的轨迹不断变化。从中可以观察到,所提出的复杂环境将更好地模拟无人机在实际应用中的场景,从而展示相关工作的研究意义,并验证目标算法的有效性、可扩展性和鲁棒性。
3.2. 目标算法与A*算法的比较
在这一部分,比较了A*算法和目标算法在具有不同数量终端用户的复杂场景下的路径差异。评估和比较了各种指标,如服务质量、平均路径长度、平均风险,并分析了它们之间的差异。
A*算法是一种在道路网络中寻找最短路径的有效直接搜索方法。对于图2(a),在固定条件下,A*算法可以到达目标点。然而,通过比较图1和图2,可以明显看出A*算法生成的路径长度明显高于提出的算法。在实际场景中,无人机的能量消耗将大幅增加。然而,从图3可以观察到,随着终端用户数量的增加,A*算法陷入了僵局,无法到达目标点。
 (a) 六个终端用户 (b) 19个终端用户
(a) 六个终端用户 (b) 19个终端用户
Figure 2. Simulation of UAV-MEC based on path planning platform with A* algorithm trajectory
图2. 基于A*算法轨迹的路径规划平台仿真无人机边缘计算系统,环境:固定障碍物,静态需求
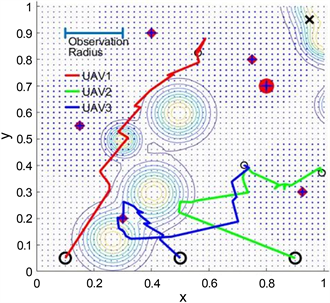
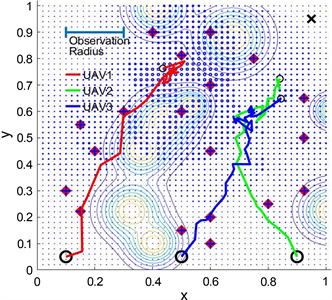 (a) 六个终端用户 (b) 19个终端用户
(a) 六个终端用户 (b) 19个终端用户
Figure 3. Simulation of UAV-MEC based on path planning platform with A* algorithm trajectory in new complex situation
图3. 基于A*算法轨迹的路径规划平台仿真无人机边缘计算在新的复杂情况下的模拟,环境:固定和移动障碍物,动态需求
表2和表3比较了A*算法和提出的目标算法在复杂情况下的无人机飞行路径规划中的性能。实验结果表明,在这些图中,由A*算法控制的无人机组在某些参数下陷入了死解中,无法到达目标点。相比之下,目标算法可以通过避开移动障碍物,有效地为终端用户提供服务,满足他们的需求,并获得更高的服务质量。

Table 3. Comparison of Key factors between target algorithm and A* algorithm in complex environment (M = 0.5, nineteen terminal users)
表3. 在复杂环境中(需求参数M = 0.5,19个终端用户),对目标算法和A*算法的关键因素进行比较
表2和表3显示了在多终端复杂环境中,提出的算法和A*算法在不同K和M值下的性能差异。比较分析主要关注三个方面,即服务质量、平均路径长度、平均风险。
表2描述了在固定需求参数M下,不同风险参数K的实验比较。实验结果表明,在低风险条件下,与提出的算法相比,A*算法表现出更高的平均路径长度、平均风险。然而,A*算法倾向于忽视终端用户的需求,导致服务质量显著降低。此外,随着风险的增加,服务质量继续下降,A*算法无法稳定地绕过移动障碍物,导致死锁和放弃一些终端需求。
表4展示了在风险参数K等于2的情况下,不同需求的实验比较。通过将风险参数设置为2,确保两种算法都能到达目标点。从表中可以看出,在服务质量方面,目标算法仍然明显优于A*算法。此外,在复杂环境中,目标算法可以保持较低的平均路径长度,同时保持更高的服务质量水平。随着需求参数的增加,A*算法牺牲了一些终端需求。然而,在这种情况下,目标算法仍然有效地为终端用户提供服务。

Table 4. Comparison of Key Factors between target algorithm and A* algorithm in complex environment (K = 2, nineteen terminal users)
表4. 在复杂环境中(风险参数K = 2,19个终端用户),对目标算法和A*算法的关键因素进行比较
通过这种比较,可以明显看出在复杂条件下,提出的目标算法仍然能够在保证无人机飞行路径较低的同时实现良好的环境适应性和高服务质量。这表明提出的算法在保证较高服务质量的同时具有路径的优势。这样的结论为无人机路径规划领域提供了有效的解决方案,并可以为无人机飞行的实际应用提供指导和参考。
4. 结论
本研究在多无人机平台的研究基础上,提出了一个新颖的环境场景,该场景与真实世界的无人机飞行条件密切相关。在之前的研究基础上进行扩展,本研究引入了新的变量,包括动态障碍物的移动性、不同的终端需求以及无人机在飞行过程中的能量消耗。利用将这些变量被纳入奖励矩阵中,以指导无人机的路径规划。这些修改增强了实验环境的真实性,使得对真实世界情景的模拟更加准确,同时验证了所提目标算法在无人机路径规划中的有效性和可靠性。实验结果表明,即使在复杂环境中,目标算法表现出很高的适应性,优于其他基准算法。此外,本研究强调了引入与真实世界环境密切相似的场景的必要性。
NOTES
*通讯作者。