蚁群算法与DBSCAN融合的仓库选址智能算法研究

Research on Intelligent Algorithm of Warehouse Location Based on Ant Colony Algorithm and DBSCAN

摘要: 正确的仓库选址，不仅能够提高运输效率，还能降低运输成本，对货物运输有着重要的作用。本文通过初始化蚁群算法距离矩阵，迭代计算不可直达客户点之间的最短距离，实现对蚁群算法的改进；相较于传统的DBSCAN聚类算法，我们将最短距离矩阵作为算法的输入，提出了基于Distance自适应的DBSCAN算法(Distance_DBSCAN)，对核心点的选择策略进行修改，实现对DBSCAN算法的改进；针对聚类结果再次利用蚁群算法，给出每一个类别的仓库选址位置和最短路径策略。实验表明，本文提出的Distance_DBSCAN算法可以正确分离噪声点，有着较好的ARI指数，且时间复杂度低，可以有效缩短聚类总路程，更重要的是此算法更加符合货物运输仓库选址的实际意义。

Abstract: The correct location of the warehouse can not only improve the transportation efficiency, but also reduce the transportation cost, which has an important role in the transportation of goods. By ini-tializing the distance matrix of ant colony algorithm and iteratively calculating the shortest distance between inaccessible customer points, this paper realizes the improvement of ant colony algorithm. Compared with the traditional DBSCAN clustering algorithm, we take the shortest Distance matrix as the input of the algorithm, and propose an Adaptive DBSCAN algorithm based on distance (Dis-tance_DBSCAN), modify the core point selection strategy, and realize the improvement of DBSCAN algorithm. According to the clustering results, the ant colony algorithm is used again to give the warehouse location and the shortest path strategy for each category. Experiments show that the Distance_DBSCAN algorithm proposed in this paper can correctly separate noise points, have a good ARI index and low time complexity, and can effectively shorten the total clustering distance. More importantly, this algorithm is more in line with the practical significance of cargo transportation warehouse location.

1. 引言

随着网络技术的发展，电商平台在近20年间呈现出了爆炸式发展，并迅速达到饱和阶段 [1] 。在竞争方向上，商品价格以及服务人群已经很难再有所突破，而面对如此庞大的物流体系，如何有效降低运输成本是目前所有电商企业、快递业务的一个重要发展方向。

1959年，Dantzig和Ramser首次提出了车辆路径(VRP)问题 [2] ，如何优化运输路径达到成本最低从此成为相关领域的研究热点。1996年Martin Ester等提出了DBSCAN算法 [3] ，该算法是一种无监督的密度聚类算法，通过基于数据点的密度来确定簇，对噪声数据也具有较好的鲁棒性，广泛应用于实际问题。同年Marco Dorigo在文献 [4] 中首次提出了使用蚁群算法(AS)来解决(VRP)问题，AS能够自适应地搜索解空间并能够有效克服局部最优解，目前已被成功地应用于TSP和VRP等组合优化问题的求解 [5] [6] [7] [8] 中。VRP问题属于组合优化问题 [9] ，是NP难问题，目前主流的解决方案有两大类：精确方法和近似方法。

精确方法 [10] [11] [12] 针对寻得全局最优解；近似方法则着力于寻得局部最优解，其在寻找过程使用的算法进一步分为近似算法和启发式算法。对于VRP问题的求解，启发式算法有着更小的算法复杂度并可以保证一定精度，在求解过程中有其优势 [13] [14] 。在这些算法的优势逐渐明晰后，国内外许多学者在DBSCAN和蚁群算法上展开研究，衍生出许多求解VRP问题的方案。徐书扬等 [15] 利用DBSCAN聚类算法对配送点进行聚类划分，根据聚类结果初始化蚁群算法参数，实现蚁群算法的改进与应用。许芳芳 [16] 提出的LF-DBSCAN算法，通过蚁群对数据集进行划分，为解决DBSCAN算法不适用密度不均匀数据集这一问题提供了思路。李静 [17] 结合蚁群优化算法和基于密度的DBSCAN算法来优化聚类效果。赵振强等 [18] 通过改进DBSCAN算法和K-means二次聚类，确定前置仓建设数量，用多重心法实现前置仓的选址。

根据本文的研究发现，大部分的实验利用DBSCAN算法中原始的距离计算方法，即计算两点之间的欧氏距离 [19] ，而在实际问题中，欧氏距离并不能很好地代表两地之间的远近。本文提出一种基于Distance自适应的DBSCAN算法(Distance_DBSCAN)，根据中国部分省会的经纬坐标作为客户点建立配送模型，并通过初始化点集、输入所有相邻点之间的路程，通过蚁群算法找到任意两点之间的最短路程，然后使用Distance_DBSCAN算法迭代判断中心点是否满足目标条件，再利用实际路程进行密度聚类，得到更贴近实际情况的聚类结果。通过此算法与普通的基于密度的DBSCAN聚类方法以及K-means聚类方法的比较，此算法的聚类效果可以得到更短的配送路程以及更合理的配送路线结果。

2. 背景简绍和算法描述

2.1. 问题背景

2.1.1. VRP问题

Versatile Routing Platform (VRP)问题即为车辆路线问题，是运筹学领域重要的研究问题之一。该问题可简述为：货物配送中心需要为一定数量，各自拥有不同的货物需求客户配送货物，并且由一个车队负责运送货物，组织适当的行车路线。而货物配送中心的目标是既能满足客户的需求，又能在一定的约束下，达到诸如路程最短、成本最小、耗费时间最少等目的。其原理图如图1：

Figure 1. VRP diagram

图1. VRP示意图

图1中D1、D2、D3为货物配送仓库中心，1~13为客户位置，通过不同的路径选择，进行各自的货物运输，达到最优目的。

2.1.2. 仓库选址问题

仓库选址问题是运筹学中经典的问题之一 [20] 。该问题可描述为在确定选址空间、选址区域和成本函数等约束条件的前提下，以总物流运输成本最低或总服务水平最优或社会效益达到最大化为目标，通过仓库位置的选择，依次来确定物流配送方案中物流节点的数量、配送顺序等信息，从而合理规划物流网络结构。

2.2. Distance_DBSCAN算法(DDBSCAN)描述

2.2.1. 蚁群算法和DBSCAN算法描述

蚁群算法(Ant Clony Optimization, ACO)是一种群智能优化算法，该算法主要是由一群蚂蚁(轻微智能个体，Agent)通过相互之间的协作(Collaboration) (通过信息素浓度(Pheromone Concentration)的积累和衰减)而表现出智能行为，从而为求解复杂优化问题提供了一个新的可能性。

DBSCAN算法是一种著名的密度聚类算法，该算法不会受到距离的影响，能够通过样本分布的紧密程度(密度)直接确定聚类结构，从样本的密度的角度来考察样本之间的相关性，并基于相关样本不断扩展聚类簇最终获得聚类结果。DBSCAN算法不仅可以处理各种分布的数据并对簇进行判定，而且还可以通过两个基本参数识别出数据集中的每个簇与噪声点。

2.2.2. DDBSCAN算法设计

(a) 改进的蚁群算法初始化距离矩阵

蚁群算法进行矩阵初始化时使用的是欧式距离(European Distance)进行直接计算，而实际货物运输过程中，直接使用欧式距离并不能代表实际问题，在改进过程中，本文通过寻找出直接相连的客户之间的实际公路路程得到邻接矩阵，并将该矩阵作为初始化矩阵输入蚁群算法中，设置蚁群算法参数使其只能通过已有的客户点，并找出不可直达的客户的最短路径，不断迭代以完善最短距离矩阵。用这一方法计算得到的最短距离矩阵，能够充分代表任意两个客户之间的实际距离。

假设t时刻客户i和客户j的距离为 $d_{ij}$ ，路径上的信息素为 ${\Upsilon }_{ij}\left(t\right)$ 。初始时刻，各个客户直接路径上信息素相同，设为 ${\Upsilon }_{ij}\left(0\right)={\Upsilon }_0$ ，设 $p_{ij}^k\left(t\right)$ 为蚂蚁k在t时刻从客户i到客户j的概率，如公式(1)所示：

$p_{ij}^k\left(t\right)=\{\begin{array}{l}\frac{{\left[{\Upsilon }_{ij}\left(t\right)\right]}^{\alpha }{\left[{\eta }_{ij}\left(t\right)\right]}^{\beta }}{{\displaystyle \underset{j\in J_k\left(i\right)}{\sum }{\left[{\Upsilon }_{ij}\left(t\right)\right]}^{\alpha }{\left[{\eta }_{ij}\left(t\right)\right]}^{\beta }}},\text{if}j\in J_k\left(i\right)\\ 0,\text{other}\end{array}$ (1)

其中 $\alpha$ 、 $\beta$ 分别为信息素和启发式因子的相对重要程度， ${\eta }_{ij}\left(t\right)$ 为t时刻的启发函数。

在蚂蚁寻优系统中，路径上的信息素浓度会随着蚂蚁离开的时间慢慢消散，也会随着下一个到来的蚂蚁释放自己的信息素而积累，令 $\rho \left(0<\rho <1\right)$ 为信息素挥发程度，m为蚂蚁总数，其信息更新表达式如公式(2)所示：

$\{\begin{array}{l}{\Upsilon }_{ij}\left(t+n\right)=\left(1-\rho \right)\times {\Upsilon }_{ij}\left(t\right)+\Delta {\Upsilon }_{ij}\hfill \\ \Delta {\Upsilon }_{ij}={\displaystyle \underset{k=1}{\overset{m}{\sum }}\Delta {\Upsilon }_{ij}^k}\hfill \end{array}$ (2)

初始化客户距离矩阵的蚁群算法运算过程：

步骤一，初始化算法参数。如蚂蚁的数量m、信息素因子 $\alpha$ 、信息素挥发因子 $\rho$ 、启发函数因子 $\beta$ 、最大迭代次数Maxiter、客户坐标、初始直达矩阵(Direct to the Matrix)等；

步骤二，进行构建解空间。即把每个蚂蚁k放置于同一个出发点，然后随机选择一个当前客户点未能直达的客户点，直到所有蚂蚁遍历完所有点，并最终到达目标点停止；

步骤三，进行信息素的更新。更新前，计算出每个蚂蚁走过的路径长度L，并记录当前的最优解bestrode，更新信息素浓度；

步骤四，判断是否终止算法。如果迭代次数少于最大迭代次数，或还存在客户之间不能连通，则清除蚂蚁走过的路径记录，迭代次数加一(iter = iter + 1)，返回步骤二，否则停止计算，输出最优解；

步骤五：输出程序结果。输出寻优过程中的相关指标，如运行时间、收敛迭代次数等，并返回最短距离矩阵(Shortest Distance Matrix)。

(b) DDBSCAN聚类

传统的DBSCAN聚类算法，在进行核心点选择时，一般是通过比较客户矩阵的距离是否小于Eps，进而直接求得核心点坐标的索引，这样算法时间较长，效率低。采用DDBSCAN算法，对核心点的选择策略进行修改，通过直接对迭代过程中产生的核心点进行判断，避免核心点被重复计算，有效地降低了核心点的寻找和判断时间，提升了算法效率。

DBSCAN聚类算法参数Eps (邻域半径)为常数，其值被赋为点与点之间的欧式距离。而在仓库选址问题中，直接使用欧式距离进行距离代表两地间的距离并不符合实际，本文改进的蚁群算法可以得到最短距离矩阵，并将其使用在DDBSCAN聚类算法的距离选择中，通过对符合实际情况的距离的迭代比较，进行聚类划分。

DBSCAN算法原理：以Eps = 2，MinPts = 6为假设条件，图2(a)中，初始化P1为第一个簇核心点；图2(b)中，以P1为核心，Eps为距离阈值，判断在最远Eps距离内可达客户点数是否满足数量大于等于6，以判断是否满足核心点条件；图2(c)中，在P1为核心的圆内，以每一个点为核心画圆，重复检验过程，发现P2满足条件，说明P1可达P2；图2(d)中，P2可达P3，而Q1在验证过程中发现不能满足MinPts ≥ 6的条件，则判定为不可达。经过以上过程本文可以得到P1通过P2可达P3的结果。

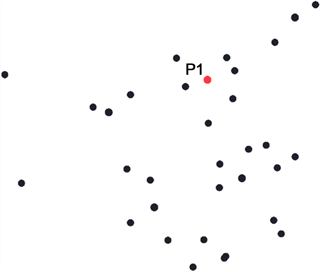
(a) 初始化聚类数据 (b) P1位置形成一个簇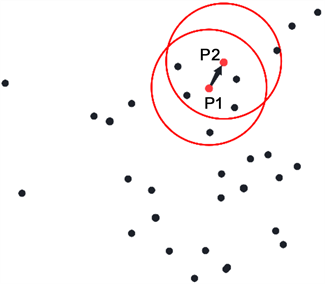 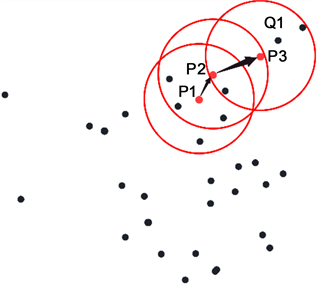(c) P2可达，转移中心 (d) P2可达，转移中心

Figure 2. DBSCAN schematic diagram

图2. DBSCAN原理图

基于蚁群算法的DDBSCAN聚类算法流程如图3。

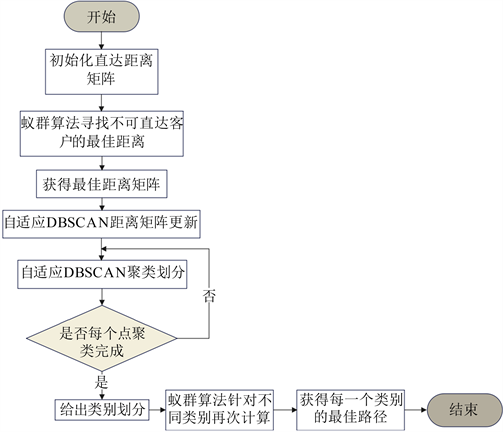
Figure 3. DDBSCAN clustering algorithm flow based on ant colony algorithm

图3. 基于蚁群算法的DDBSCAN聚类算法流程

DDBSCAN算法聚类伪代码如下所示：

DDBSCAN整体算法摘要：

3. 实验内容和结果分析

3.1. 问题评价指标

为了评价聚类效果好坏，本文引入以下评价指标，用于检测聚类效果的优劣。

3.1.1. 轮廓系数 [21]

轮廓系数(Silhouette Coefficient, SI)是描述聚类后各个类别的轮廓清晰度的指标。其包含有两种因素——内聚度和分离度，轮廓系数的计算方法如公式(3)所示：

$S\left(i\right)=\frac{b\left(i\right)-a\left(i\right)}{\max \left\{a\left(i\right),b\left(i\right)\right\}}$ (3)

其中 $a\left(i\right)$ 代表内聚度，可通过公式(4)计算：

$a\left(i\right)=\frac{1}{n-1}{\displaystyle \underset{j\ne 1}{\overset{n}{\sum }}dis}\left(i,j\right)$ (4)

j是与样本i在同一个类内的其他样本点， $dis\left(i,j\right)$ 代表i与j的距离。而 $b\left(i\right)$ 需要遍历其他簇得到多个值 $\left\{b_1\left(i\right),\cdots ,b_m\left(i\right)\right\}$ ，并从中选择最小的值作为结果。

所以， $S\left(i\right)$ 可进一步简化为公式(5)：

$S\left(i\right)=\{\begin{array}{l}1-\frac{a\left(i\right)}{b\left(i\right)}a\left(i\right)<b\left(i\right)\hfill \\ 0a\left(i\right)=b\left(i\right)\hfill \\ \frac{b\left(i\right)}{a\left(i\right)}-1a\left(i\right)>b\left(i\right)\hfill \end{array}$ (5)

轮廓系数 $S\left(i\right)\in \left[-1,1\right]$ ，数值越大聚类效果越好。

3.1.2. 噪声比

聚类噪声比是指在聚类过程中，噪声点占整个数据集的比例。它是评估聚类算法性能的一个重要指标之一，通常噪声比越小越好。

3.1.3. 调节的兰德指数 [19]

给定n个对象集合， $S=\left\{O_1,O_2,\cdots ,O_n\right\}$ ，假设 $U=\left\{u_1,u_2,\cdots ,u_R\right\}$ 和 $V=\left\{v_1,v_2,\cdots ,v_C\right\}$ 表示S的连个不同划分，且满足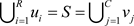， $u_i\cap u_i^{\ast }=\varnothing =v_j\cap v_j^{\ast }$ 其中 $1\le i\ne i^{\ast }\le R$ ， $1\le j\ne j^{\ast }\le C$ 。

其中兰德系数(R)：

$R=\frac{a+b}{C_n^2}$ (6)

其中n为样本总数。

调节的兰德指数(Adjusted Rand Index, ARI)又称调整兰德系数，调整兰德系数假设模型的超分布为随机模型，即U和V的划分为随机的，那么各类别和各簇的数据点数目是固定的，不会随聚类标签变化而变化，计算方法如公式(7)所示：

$\text{ARI}=\frac{RI-E\left(RI\right)}{\max \left(RI\right)-E\left(RI\right)}$ (7)

其中ARI取值范围为[−1, 1]，值越接近1，聚类效果越好。

3.2. 初始数据和算法参数

初始数据集属性见表1，在本文的数据集中，共有30个数据点，划分为5类。

Table 1. Properties of the dataset

表1. 数据集属性

蚁群算法部分参数与初始化数据见表2，根据客户数量和距离矩阵，设置相应的参数，其中*为可变参数，其余为实验建议参数。

Table 2. Parameters of the ant colony algorithm

表2. 蚁群算法参数

3.3. DDBSCAN算法结果

图4(a)中，使用实际距离的初始化矩阵，迭代500次后，平均路径长度和最佳路径长度如图所示，可以看出算法迭代到约270轮左右达到最佳，最佳路程为19,587；图4(b)为全局最短路径示意图。

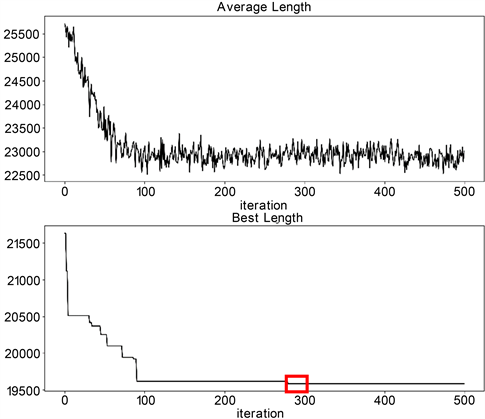(a) 改进的蚁群算法迭代过程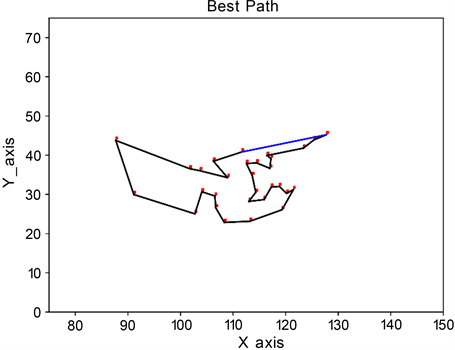(b) 改进的蚁群算法总数据路径

Figure 4. Iterative process of the improved ACO algorithm

图4. 改进的蚁群算法迭代过程

DDBSCAN对30个客户最终聚类结果如图5所示：

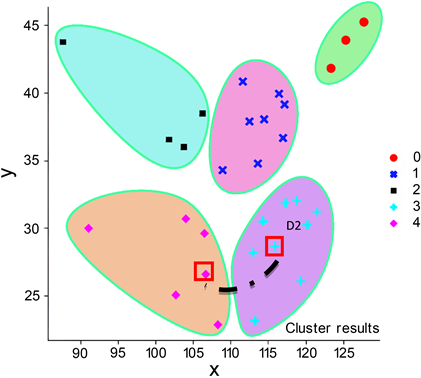
Figure 5. DDBSCAN clustering results

图5. DDBSCAN聚类结果

使用DDBSCAN进行聚类，并将噪声点进行归类，完成仓库聚类选址问题，在图中一共分为5类，仓库位置可选择在同一个聚类点的任何位置，为了最优化上一层运输到仓库问题，可选择类与类之间相对较近的点最为该类的仓库点，如图5中的D1和D2。

图6更进一步展示DDBSCAN聚类距离效果，使用蚁群算法重新进行类间距离寻找，路线如图6所示，最后计算得到总路程为19,030。

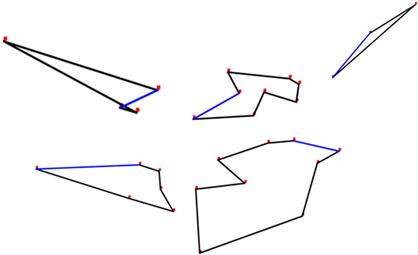
Figure 6. Shortest path obtained by ant colony algorithm after DDBSCAN clustering

图6. DDBSCAN聚类后蚁群算法获得最短路径

K-means算法在对数据集进行聚类时，将所有数据点作为计算对象，在聚类结果中不存在噪声点，在一个类内部的类内元素紧密程度小，内聚度小；而在DBSCAN算法和DDBSCAN算法计算轮廓系数时，噪声点并不在任何一个类内部，使这两种算法的内聚度大；则K-means有较好的轮廓系数。而在ARI分数上，DDBSCAN算法得到的聚类结果与理想的结果最为接近，分数相较于K-means算法有较大的提升，同时，DDBSCAN算法的时间复杂度较低，详细数据见表3。

Table 3. Comparison of algorithm performance

表3. 算法性能对比

蚁群算法通过启发式寻找优化出总路程为19,587，经过DDBSCAN算法聚类得到的总路程为19,030，相较于直接使用蚁群算法总路程减少557，且每一个类中的路径总路程均小于或等于K-means算法结果，见表4。综合表3和表4可以说明该算法具有一定的优势。

Table 4. Shortest path distance comparison

表4. 最短路径路程对比

4. 结语

针对实际仓库选址问题，本文提出基于Distance自适应的DBSCAN算法(DDBSCAN)，通过提供客户点两两直达的初始路程矩阵，针对蚁群算法的初始信息矩阵进行更新，进一步求解出初始客户之间未能两两直达的距离，通过不断迭代，获得最短距离全连接矩阵，随后使用DDBSCAN聚类算法。首先对算法的距离矩阵进行替换，随后在聚类的过程中，更改以往的聚类核心点选择策略，从而提高算法聚类效率，最后将噪声点归类，获得最终聚类结果并再次利用蚁群算法计算每一类的总路径路程，通过比较各个算法的性能和路程，证明了本文的DDBSCAN算法更突出，可以正确分离噪声点，时间复杂度低，对聚类结果、总路程均有改善，且更加符合实际仓库选址问题。考虑到数据点数量问题，本文只针对30个全国抽象出来的4S店进行测试实验，在后期的处理过程中可收集更多的仓库数据点，其次在蚁群算法迭代过程中，可进行多次参数调节，以获得最佳参数。

基金项目

吉林省自然科学基金自由探索重点项目(YDZJ202201ZYTS585)；

吉林省创新能力建设项目(2022C047-2)。

NOTES

^*第一作者。

^#通讯作者。