1. 引言
随着科技的发展,特别是在计算机和工业自动化等领域,离散采样控制得到了较好的发展。在现代系统应用中,高速采样的方法越来越重要。但是在高速采样下,用位移算子描述的离散系统经常会出现数值不稳定的现象,这也是众多学者寻求其他描述方法的动力和源泉。20世纪80年代中期Goodwin和Middleton [1] 提出采用Delta算子来描述离散时间系统,并引入对应于Delta算子的Delta变换,恰好避免了位移算子算带来的弊端。鉴于Delta算子的诸多优点,国内外学者对Delta算子系统理论的研究从未间断。2005年,李惠光 [2] 等学者编著了国内首部研究Delta算子系统的专著,详细地介绍了Delta算子系统理论。肖民卿等人研究了Delta算子系统的非脆弱方差控制 [3] 、带故障的鲁棒H∞控制 [4] 和Delta算子时滞系统的可靠D-稳定 [5] 。Yang [6] 等人提出与了改善执行器饱和的Delta算子系统反馈控制的新方法,并研究了Delta算子系统的鲁棒容错控制问题。
而切换系统主要的研究方向包括系统的稳定性、能控性以及能观性等其他综合性问题,其中切换系统的稳定性是切换系统研究的热点问题之一,也是研究切换系统其他控制问题的前提条件。切换系统的常用研究方法主要分为公共Lyapunov方法 [7] 、多Lyapunov方法 [8] 以及驻留时间方法 [9] 等。
Delta算子切换系统可以看作是每个子系统都是Delta算子系统的切换系统。切换系统是处理复杂系统问题较为优异的模型,Delta算子切换系统的研究得到了控制界学者的关注,并取得了一些进展。向峥嵘等人基于平均驻留方法,给出了不确定Delta算子切换系统指数稳定的充分条件 [10] ,并研究了鲁棒滤波器 [11] 和其他鲁棒控制问题 [12] 。Hu等人基于多Lyapunov方法和凸组合方法,研究了Delta算子切换系统的可靠极点配置 [13] 容错控制 [14] 及非脆弱可靠D-稳定 [15] 等问题,创新性的引入一阶LMI区域,推动了区域极点配置理论的发展。
本文在第2节中对所研究的Delta算子时滞切换系统的非脆弱H∞控制问题进行了描述。第3节利用线性矩阵不等式(LMI)方法和Lyapunov稳定性理论,研究了系统渐进稳定和存在
-次优非脆弱H∞控制律的条件,并设计了非脆弱H∞控制控制器,最后进行数值仿真验证了这个结论的可行性。
符号说明:
代表实数域,
代表n维欧几里得空间,
表示维数为
的所有实矩阵集合。
表示矩阵
的转置,
表示矩阵
的逆。
表示适当阶数的单位矩阵,
表示适当阶数的零矩阵。对称矩阵中的“*”表示矩阵相应的对称分块。
(
)表示矩阵
是对称正(负)定矩阵,
(
)表示矩阵
是对称半正(负)定矩阵,对于两个矩阵
,
(
)表示矩阵
是正定(半正定)。
表示向量的欧几里得范数,
表示矩阵的谱范数。
为了解决下文中的问题,提前给出下面两个引理。
引理1 [16] 对给定矩阵
,其中
是
的,以下三个条件等价:
1)
;
2)
;
3)
,
。
引理2 [16] 给定适当维数的矩阵Y,D和E,其中Y是对称的,则对所有满足
的矩阵F,
成立当且仅当存在一个常数
,使得
2. 问题描述
Delta算子定义为:
其中q为前向位移算子,即
,h为系统采样周期。
考虑一类由Delta描述的不确定时滞切换系统:
(1)
其中:
是切换律,
,
、
和
分别为系统的状态、控制输入和外部扰动输入且
,
是被调输出,T为采样周期,d是系统的状态滞后时间,假定
,
、
、
、
、
和
是已知的适当维数的实常数矩阵,
、
、
、
、
和
是不确定矩阵,表示系统模型中的不确定参数,且满足:
(2)
(3)
其中对任意
,不确定
,满足
。
、
、
、
、
、
、
和
为组成不确定性结构的适维常数矩阵。
采用状态反馈控制,并假定控制器具有加性增益不确定性,具体如下:
(4)
其中:
(5)
和
为已知的适维常数矩阵,
是满足
的不确定矩阵。得到闭环系统为:
(6)
其中:
定义1 对给定的正数
,如果对所有满足(2)、(3)和(5)的不确定参数,闭环系统(6)是渐进稳定的,且在零初始条件下,被调输出
满足
,则状态反馈控制律(4)称为是系统(1)的
-次优非脆弱H∞控制律。
3. 主要结论
定理1 对给定正数
,任意的
,系统(1)存在
-次优非脆弱H∞控制律(4)的一个充分条件是存在对称正定矩阵P和Q,使得对所有允许的不确定参数,下列矩阵不等式成立:
(7)
证明 考虑Lyapunov函数
(8)
其中,
,
。
在
时,由
可得
将上面两式相加代入(8)中可得
其中,
。
由引理1可得
(9)
再由引理1的变化后,矩阵不等式(7)成立可知矩阵不等式(9) < 0也成立。
因此,
,故闭环系统(6)在任意切换律下是渐进稳定的。
进而,对任意非零的
,
利用引理1可得,矩阵不等式(6)成立时有
,对
由零初始条件可得,
,对
由此可得
。定理得证。
定理2 对给定的正数
,任意
,存在对称正定矩阵P和Q,使得对任意允许的系数参数不确定性和控制器增益不确定性,矩阵不等式(6)成立,当存在大于零的常数
,
,
,对正定矩阵X,V和W使得如下线性矩阵不等式可行:
(10)
其中:
且
是系统(1)的一个
-次优非脆弱H∞控制律,其中
。
证明 矩阵不等式(7)可以写成
(11)
其中:
根据引理2,对所有允许的不确定矩阵
,(11)式成立的一个充要条件是存在
,使得
(12)
由引理1及一些等价变化可得(12)式等价于
(13)
其中:
根据引理2,对所有允许的不确定矩阵
,(13)式成立的一个充要条件是存在 ,
,使得
(14)
由引理1及一些等价变形可得(14)式等价于
(15)
其中:
将上式两边分别左乘、右乘
,并记
,
,
,
,即可得到(10)式。
4. 数值算例
给定由两个子系统组成的系统(6),其中
采样周期
,滞后上界
。根据定理2提出的设计方法,对给定的正数
,应用 的LMI工具箱中的求解器feasp求解线性矩阵不等式(10),得到可行解为:
从而可得:
设系统初始状态
,外部扰动
,给定任意一个切换律(如图1所示),得到闭环系统状态轨迹如图2所示。
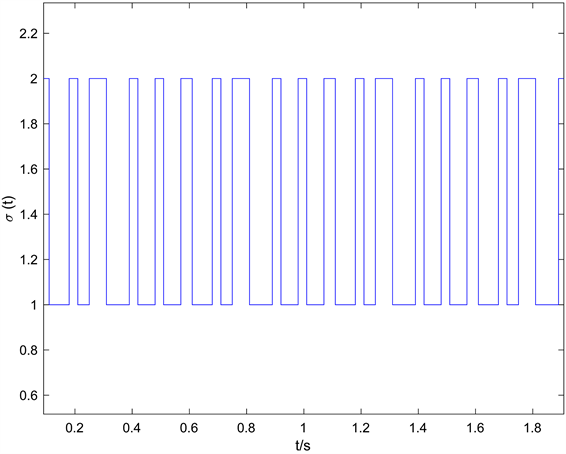
Figure 2. The state trajectories of the closed-loop system
图2. 闭环系统状态轨迹
5. 总结与展望
本文利用LMI方法及公共Lyapunov稳定性理论对Delta算子时滞切换系统设计了具有非脆弱的 控制器,使得在任意切换律下的Delta算子时滞切换系统都是渐进稳定的。
虽然取得了一些成果,但仍然存在一些问题值得进一步思考。研究的控制约束是线性系统,非线性系统方面还未涉及。运用公共Lyapunov函数和线性矩阵不等式方法,对于是否可以利用多Lyapunov函数和平均驻留时间方法来研究该方面的问题,需要进一步探讨。