有软壳海洋生物附着圆形柱体的涡激振动的影响研究

Experimental Studies on Vortex-Induced Vibrations of a Circular Cylinder Covered with Soft Marine Growth

摘要: 伴随着海上资源的开发，越来越多的海上设施出现。研究对水下构筑物状态的影响因素对海上设施的设计具有重要意义。随着研究的深入，海洋生物的附着对近海建筑物的水下结构物的污染受到更多的关注，其中，附着的海洋生物可以分为硬壳海洋生物和软壳海洋生物两大类。以往的研究大多是模拟硬壳海洋生物的附着对象。作为对已有研究的补充，本文的研究对象为附着有软壳海洋生物的圆柱体。通过设置对照试验，研究不同长度和间隙比的海洋软壳生物的动力响应，包括阻力和旋涡脱落特性。制作6个实验组模型的方法是在长为125 cm，宽为20 cm柔软的薄膜上在特定位置切割孔来固定宽度为1.5 cm彩带，将彩带和薄膜覆盖在直径为6 cm，长130 cm的圆柱形钢管上。考虑间隙比分别为0.5 D和0.8 D，长度分别为0.5 D、1 D和2 D (D为圆柱形钢管直径)。对照组则是由圆柱形钢管和只覆盖薄膜的圆柱形钢管组成。所有实验均在位于西澳大利亚大学结构实验室的风洞中进行。通过不同的软件记录原始数据，并使用MATLAB和EasyPlot进行数据处理。所有结果在汇总后，利用Prism绘制图表。将各实验组模型的计算结果与对照组模型的计算结果进行了比较。研究发现，用于模拟的软壳海洋生物的彩带会使模型受到更大阻力的同时也抑制涡激振动。研究拓展了海洋生物附着对圆柱结构所受阻力和涡激振动的认识。

Abstract: With the development of the technique, more and more offshore facilities appear. It is important to study the influence of various factors on the state of structures underwater for the design for the offshore facilities. With further research, the effect of marine pollution on construction has become popular. Marine pollution is manifested as organisms in the ocean clinging to underwater structures in offshore buildings and the marine organisms are divided into two main categories, hard marine and soft marine. Most of the previous studies had simulated the attachment object of hard marine. As a supplement to existing research, the object of the research was the circular cyl-inder covered with soft marine growth. The hydrodynamic responses, force and vortex shedding characteristics, of soft marine with different lengths and gap ratios are studied by setting up control experiment. The method of six models made was that cutting holes at specific positions on the 125 cm long, 20 cm wide soft film and fixing the 1.5 cm wide ribbon then covering the film with ribbon on steel circular cylinder. The diameter of the cylinder is 6 cm and the length is 130 cm. The gap ratio is 0.5 D and 0.8 D respectively and the length is 0.5 D, 1 D and 2 D respectively (D is the diameter of the steel circular cylinder). The control group consisted of a steel circular cylinder and a steel circular cylinder covered only with a film. All experiments were conducted in a wind tunnel located in the Structural Laboratory of the University of Western Australia. The raw data was recorded by different software and processed using MATLAB and EasyPlot. All the results are summarized and plotted using Gnuplot. The calculation results of each experimental group model were compared with those of the control group model. It was found that the ribbon of soft-shell Marine organisms used in the simulation subjected the model to greater drag while also suppressing vortex-induced vibration. This study expands the understanding of the drag force and vortex- induced vibration of steel cylinder covered by soft marine growth.

1. 引言

无论是开发海洋中的化石能源还是新能源，都离不开海上建筑的支持。化石资源的开采需要钻井平台，新能源的开发，例如风电场，也需要水下基础支撑发电机。在2016年，离岸生产的石油和天然气占全球油气产供应的四分之一以上，并且在到2040年的预测中，与能源相关的海上活动的数量将增加 [1] 。由于传统能源带来的环境问题，新能源越来越受欢迎。基于技术等原因，潮汐能仍处于起步阶段，现阶段只有少数国家正在进行试验 [2] 。与潮汐能不同，风能发展迅速并且发展前景被人们看好 [3] 。例如，在美国新泽西州大西洋城，一个拟议中的公用事业规模的海上风电场位于外大陆架 [4] ；德国的阿尔法文图斯离海岸约15英里的风力发电场，计划可以供应大约50,000个家庭 [5] 。

在开发海洋能源的过程中，海上设施是不可缺少的。这些建筑在海中会遇到以下两种问题。首先受到涡激振动的影响。涡激振动是一种流激振动。对于单个圆柱体的涡激振动研究之前就比较完善了，例如，Sarpkaya对近二十年来受稳定均匀流作用的圆柱结构的涡激振动(VIV)的研究进展进行了综述 [6] ，Williamson综述了有关涡激振动的基本结果并提出了新的涡尾流模式 [7] [8] 。涡激振动产生于当物体的旋涡脱落频率与固有频率相同时发生的共振。在流体动力学中，涡激振动是由于外部流体流动相互作用的物体引起的运动，由该流动的周期性不规则性产生或产生运动。它是造成结构疲劳的主要原因之一。疲劳失效会缩短了建筑物的使用寿命。圆柱形结构是海洋工程中常见的结构形式，包括管道、桅杆、桥梁和港口立管和海底电缆等。近几年对此结构的研究引起了人们的关注，例如Abdelhady指出在许多应用中一根绞合电缆通常被认为具有与圆柱相同的流量特性 [9] ，J.G. Tom研究了无外加流体时振荡的圆柱体的流体动力学 [10] ，Chenltin Sun进行了不锈钢筛网制成的网格卷成圆柱形的尾流研究 [11] ，Rodríguez采用大涡模拟方法研究了圆柱流动的拓扑结构和旋涡脱落过程 [12] 。其次，在海洋环境中，暴露在海水中的建筑物极易受到海洋生物的侵害。随着时间的推移，海洋生物在结构上的积累变得更厚，改变结构的表面状况 [13] 。这也会改变结构的流体力学性质，这会对海上结构产生影响。对此也有对于海洋生物的积累导致结构粗糙度比的改变进行研究，例如Chenlin Sun研究了表面粗糙度高度(k/D)对圆柱尾流特性的影响 [14] ，Gao研究了表面粗糙度对固定平面壁面附近圆柱涡激振动(VIV)响应的影响 [15] 。此外虽然附着在结构上的海洋生物种类很多，但大致可以分为硬壳海洋生物和软壳海洋生物 [16] 。所以也由对特定海洋生物造成影响的研究，如Afshar对硬壳海洋生物(藤壶)进行了研究 [17] 。作为对之前的研究的补充，本研究的研究对象是被软壳海洋生物附着的圆柱体。通过设置对照实验并且制作实验模型模拟不同长度和间隙比的软壳海洋生物的附着情况。实验采用彩带来模拟软壳海洋生物。通过改变彩带的长度和间隙比来体现的软壳海洋生物的生长情况的变化。实验在西澳大利亚大学结构实验室的风洞中进行。实验通过对比不同模型在的匀速风速下的响应的数据得出结论。目前的分析主要集中在彩带对于模型流体力学性质的影响和对于模型涡激振动的影响。

2. 实验设置

2.1. 实验室介绍

所有的实验都是在西澳大利亚大学的风洞实验室中进行的。风洞实验室的尺寸是长6 m，宽2.8 m，高2.2 m。其中试验台的尺寸是长2.5 m，宽1.32 m，高1.6 m。风洞的风速由频率控制器控制调节。控制器中显示的频率和风洞中的风速的关系如下：

$U=0.1726\times F_{requency}Hz-0.06956$

其中，U为风速，F_requency为控制器中显示的频率。

2.2. 实验模型的制作

实验主要研究软壳海洋生物的长度和密度的变化对被附着的圆柱形结构的影响。为了精确的控制软壳海洋生物的长度和密度的变化，采用模拟实验的方法。

在实验中选用彩带来模拟软壳生物的原因是，彩带可以模拟出软壳生物柔软并且其自身的长度不可忽略的特点。同时可以和硬壳生物有很明显的区分。所以制作有彩带的圆柱形钢管的模型来模拟现实中软壳海洋生物附着圆形柱体。

模型的制作的方法是在薄膜不同间隔的位置上划开一个洞然后把彩带固定在薄膜上。

在对照试验中，实验组模型一共有六个，分别为长度为0.5 D (D为圆柱体直径)、1 D和2 D，间隙比为0.5 D和0.8 D。两个对照组模型分别是裸露的圆柱管和只覆盖薄膜的圆柱管(后文中分别称为裸管和空管)。考虑到薄膜对圆柱体的表面粗糙度和直径影响，薄膜越柔软越薄，它对结果的干扰越小。结合试验台的尺寸，实验中采用长130 cm，直径为6 cm的圆柱空心钢管。薄膜的尺寸设计为长125 cm，宽20 cm，覆盖率为96%。薄膜长度小于钢管的原因是模型在进行力学实验时需要搭载两侧的力学传感器上，震动实验时需要与弹簧相连并且安装挡板。薄膜宽度大于钢管周长(约18.85厘米)的原因是需要用双面胶带将薄膜固定在钢管上，多余的部分使附着效果更好。虽然它会增加薄膜接头的厚度。彩带的宽度为15 mm。材质接近丝绸。

2.3. 实验过程

2.3.1. 力学实验

在本实验中用于记录力学数据的是一对力学传感器如图1，被安装在试验台的两侧，距离试验台的底部66 cm。

Figure 1. Load cell

图1. 传感器

用于实验的圆柱体的直径是6 cm，直径和距离的比值是11，远远大于底部对于主体的影响临界值0.2。这个数值在Guanghao Chen [18] 和Bearman [19] 的实验中被证实。所以在本实验中这这个影响被忽略。

为了减少薄膜接头处厚度增加的影响，在安装模型时，将关节放置在模型的背风处。

实验模型的安装如图2所示。

Figure 2. Experimental diagram with different gap ratio

图2. 不同间隙比的实验图

实验中产生的数据由电脑中的ATI DAQ软件记录。记录的数据中，只对圆柱体所受到的垂直于和平行于风的方向的力进行分析。受制于风洞实验室，风速范围从14 Hz至50 Hz，间隔4 Hz。当风速稳定时，收集测压元件的数据的时间为三分钟，并对每一个风速进行重复进行。

2.3.2. 涡激振动实验

在本实验中，模型用四个弹簧固定在试验台上。如图3。

Figure 3. The experimental model is mounted on the test bench

图3. 实验模型安装在试验台上

为了保证模型的震动发生在垂直于风的方向上，所选用的四个弹簧的长度和弹性模量相同。在钢筒后面安装了一个挡板，墙上安装的射线记录模型振动中的高度变化。如图4。

Figure 4. Photo of the position between baffle and ray

图4. 射线的安装位置图

安装完毕后，再用水平仪测量，来保证模型和挡板都是水平的。数据由DigiDAQ软件记录。记录的采样率是3200 Hz，时间长度是45 s。在实验过程中，模型震动的最大高度应该小于弹簧的伸长量，保证记录的数据准确性。

每一个模型的实验起始风速由模型的自振频率决定。本实验中确定模型固有频率的方法是，在安装模型后通过敲击模型，使模型上下震动。通过在MALTAB中对记录到的数据进行快速傅里叶转换，将输出的文件用easy plot展示，通过找到图中峰值对应的纵坐标来确定模型的固有频率。如图5所示。

对于涡激振动实验，在本研究中只分析模型开始震动之前到图像中出现第一个峰值后的震动基本稳定阶段的数据。

Figure 5. Image of natural frequency for bare model

图5. 裸管模型的固有频率图像

3. 实验数据的处理方法

力学实验

本实验中主要分析不同模型，研究斯特劳哈尔数，阻力系数和升力系数和雷诺数的变化关系。雷诺数的计算公式如下：

$Re=\frac{UD}{\gamma }$

其中，Re是雷诺数，U是风速，D是圆柱钢管的直径，γ是风洞实验室中的空气的运动粘度是1.5 × 10⁻⁵ m²/s。

采用雷诺数来代替风速是因为雷诺数可以消除实验中流动介质是风的局限性。速度和雷诺数的数据如表1所示。雷诺数的范围是9387.36~34241.76。

Table 1. The relationship between Reynolds number and wind velocity in force test

表1. 力学试验中雷诺数与风速的关系

斯特劳哈尔数(Strouhal Number)的公式如下

$S_t=\frac{f_{s}D}{U}$

其中，S_t斯特劳哈尔数，f_s是脱落频率，D是圆柱钢管直径，U是风速。

脱落频率的获得是通过对测得的升力进行快速傅里叶变换(FFT)。实验中用MATLAB对原始数据进行处理，在输出文件中找到峰值。峰值对应的频率为脱落频率。

阻力系数的公式如下

$F_D=\frac{1}{2}\rho C_D{U}^{2}A$

其中F_D是阻力，ρ是空气的密度，C_D是阻力系数，U是风速，A是迎风面的面积。

4. 涡激振动实验

如果旋涡脱落频率与物体的固有频率相同，就会发生共振，这就是涡激振动。本实验通过分析不同模型在发生共振时的最大振幅和引发震动的开始速度得出结论。实验中的收集的数据在easy plot中如图6所示。

Figure 6. Presentation of data in EasyPlot (0.8 D gap 0.5 length model in VIV test)

图6. EasyPlot中数据的表示(VIV测试中0.8 D间隙0.5长度模型)

通过图中所示图像，可以发现同一风速下向上的振幅会比向下的振幅略小。原因是模型震动时还会受到重力的影响。在分析数据时，采用平均振动振幅来表示在特定风速下记录的振幅的。对于每一个固定风速，各区域最大高度10%以内的平均高度为该区域的平均高度(均为绝对值)。平均振动幅值为两个区域的平均值。这个方法可以消除重力对于振幅的影响。

每次涡激振动试验的起始风速由模型的自振频率决定。方法如前文所说。固有频率的计算结果见表2。通过代入频率，计算出共振所需的近似风速。在此基础上，将初始风速降低2~3个单位(Hz)。风速间隔为1个单位，记录时间为风速稳定后的3分钟。当振幅随风速变化不明显时，测试结束。

Table 2. The results of natural frequency for every model

表2. 每个模型的固有频率的结果

5. 分析

5.1. 力学实验

在力学实验中通过比较不同模型在特定雷诺数下的斯特劳哈尔数和阻力系数的变化来得出结论。

从图7中可以看出，对照组中裸管(Bare)和空管(Empty)斯特劳哈尔数基本相同，大约是0.2。这与Schewe, G. [20] 得出的实验结果相同。这意味着薄膜对于圆柱钢管的影响可以忽略不计。此外在每一个相同的雷诺数下，实验组模型的斯特罗哈尔数都低于对照组的斯特罗哈尔数。这说明彩带的存在降低了斯特罗哈尔数的值。更具体地说，这种作用体现在彩带的长度和间隙比上，从图中可以看出，相同彩带长度下，间隙比小的模型的斯特罗哈尔数小于间隙比大的模型。同样的，相同间隙比，彩带长度长的模型的斯特罗哈尔数小于彩带长度短的模型。

Figure 7. Comparison of Strouhal number

图7. Strouhal数的比较

理论上，一个模型的斯特罗哈尔数不随雷诺数的增加而变化。从图7可以看出，对照组中除了间隙比等于0.5 D，长度等于0.5 D模型的实验结果与理论一致外，其余五组数据在雷诺数等于23195.36之前，斯特罗哈尔数有增加的趋势，在此之后斯特罗哈尔数保持稳定。这与理论不符。实验中观察到的现象可以很好地解释这一现象。在测试中，模型迎风侧的彩带受到风的影响，产生向钢筒靠近的倾向。随着风速的增加，这一趋势得到了加强。现在这个模型看起来像一个带有流线型尾巴的圆柱体。

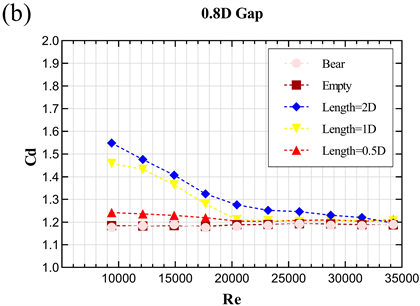
Figure 8. Comparison of the drag coefficient

图8. 阻力系数比较

比较图8中的数据，对照组中两个模型的结果基本相同。这意味着在阻力系数分析中同样可以忽略薄膜带来的影响。在每个雷诺数下的实验组模型的阻力系数都对照组的阻力系数大。因此，彩带的存在增加了阻力系数的值。换句话说，彩带增加了风对模型的阻力。更详细的说，图8(a)和图8(b)中，在相同的间隙比下，彩带的长度的增加会导致阻力系数的增加。综合图8中两幅图来看，当彩带的长度一定时，间隙比的减小对阻力系数的增加也有明显的影响。综上所述，彩带长度的增加和间隙比的降低都会增大阻力系数。

与斯特罗哈尔数一样，理论上阻力系数也不随雷诺数的增加而变化。对照组和两个0.5 D长度模型的实验结果与理论一致。但从1 D长度模型和2 D长度模型的结果来看，当雷诺数小于23195.36时，阻力系数随雷诺数的增加而减小，当雷诺数大于23195.36时，阻力系数基本保持在一个固定值。如前所述，这种非理论的变化是由风速的增加引起的模型的形状改变所引起的。所以对于设计有软壳生物的结构时，考虑潜在的形状改变是有必要的。

5.2. 涡激振动实验

在涡激振动实验中，通过在不同折合速度下通过比较归一化幅度和自锁区域的变化来得出结论。

图9的横纵坐标分别是折合速度和归一化幅度。折合速度(reduced velocity)和归一化振幅速度(normalized amplitude)为

$V_r=\frac{U}{f_{n}D}$

$归一化振幅速度=\frac{A}{D}$

其中，A是平均振幅，D是圆管的直径，V_r是折合速度，U是风速，f_n是模型的自振频率。

首先，分析对照组模型的数据。如图9(a)所示，在裸管的模型数据里，归一化振幅的最大值为0.603，在空管的模型的数据中，归一化振幅的最大值为0.555，减小了7.96%。裸管的开始振动的折合速度为5.639 m/s，空管的模型的开始振动的折合速度为5.293 m/s。折合速度降低0.346 m/s。虽然薄膜带来的影响很小，但是在图9(b)和图9(c)中，用空管的数据来和实验组数据进行对比来保证实验变量的唯一。

总体来看彩带的存在使模型最大归一化幅度明显降低。如图9(b)和图9(c)所示，模型的间隙比相同时，彩带长度的增加会使模型最大归一化幅度的峰值降低。如表3所示，而对于相同彩带长度的的模型，振幅的峰值随着间隙比减小而减小，但是减小的程度很小。

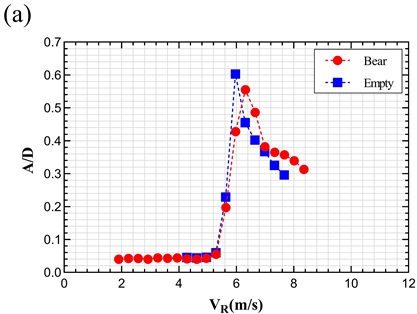
Figure 9. Comparison of the normalized amplitude

图9. 归一化振幅速度的比较

Table 3. Maximum normalization amplitude in different models

表3. 不同模型的最大归一化幅度

其中最大归一化幅度减小的潜在原因是彩带破坏了原有的涡结构。在另一个实验中，将模型放入水槽中，使恒定的流速流经模型。实验照片如图10所示。

Figure 10. The photo of PIV (Notice the top left corner of the picture)

图10. PIV的照片(注意图片的左上角)

从图10可以看出，随着彩带长度的增加，振动的起始点有延迟的趋势。需要注意的是，长度等于5 D的模型和长度等于1 D的模型的起始点在视觉效果上出现重叠。前者开始振动的减速速度为6.058 m/s，后者开始振动的减速速度为5.710 m/s。这与趋势是一致的。

综合以上分析可知，随着带长度的增加和间隙比的减小，最大平均振动幅值减小，振动起始延迟到更高的减速速度。

下一个分析是锁定区域。如果脱落频率与结构固有频率之比等于1，则意味着脱落频率与结构的特征频率匹配，发生锁定情况。根据锁定区域的定义，绘制如下图11。分析了不同模型的锁域范围和时间。

Figure 11. Lock-in region for different models

图11. 不同模型的锁定区域

如图11所示，对照组的模型在锁定前数据和St = 0.2平行，说明他们的斯特劳哈尔数也是0.2。这与理论相符。

将图11中的部分信息由表4展示，可以很容易地发现折合速度区间在减小。结果表明，锁定区有缩小的趋势。通过对裸管和空管模型的比较，发现即使是薄膜也对锁定域的减小有不可忽略的影响。空管模型和实验组模型进行比较，彩带长度的增加和间隙比的减小会缩小锁定区域。彩带还抑制了锁相区的起始降低速度。这与上文的结论是一致的。

Table 4. Detail of the lock-in region for different models

表4. 不同模型的锁定区域数据

6. 结论

本文用设置对照实验的方法，通过利用彩带模拟软壳海洋生物的生长情况来探究软壳海洋生物的附着对圆柱形结构的影响。值得注意的是，彩带在不断增加的风速下出现了外形改变的现象。在到达一定雷诺数之前，彩带会随着流体的流向改变位置。产生最直接的影响就是阻力系数的变化。这是软壳海洋生物与硬壳海洋生物的区别之一。在设计实验时应当注意。

研究表明，彩带的长度和间隙比会影响模型的流体力学特性和涡激振动。这也就意味着软壳海洋生物的附着会使柱体的流体力学特性和涡激振动发生改变。

其中流体力学特性的变化体现在：

1) 软壳海洋生物的附着会使被附着的圆柱体的斯特劳哈尔数值的降低。彩带长度的增加和间隙比的减少会加剧这一现象。

2) 软壳海洋生物的附着会使被附着的圆柱体的阻力系数和阻力增加。彩带长度的增加和间隙比的减少会加剧这一现象。

涡激振动的变化体现在：

1) 软壳海洋生物的附着会使被附着的圆柱体的最大归一化幅度降低。彩带长度的增加和间隙比的减少会加剧这一现象。

2) 软壳海洋生物的附着会使被附着的圆柱体振动的起始点被延迟到更高的减速速度。彩带长度和间隙比的变化虽然对这种现象的影响比较小，但是彩带长度的增加和间隙比的减少会延迟振动的起始点。