1. 引言
股权是指股东通过购买公司的股票,成为公司的股东,从而享有相应的权益和利益。股权的大小取决于股东所持有的股票数量。
权力应用充斥于日常各类社会关系中,引起许多学者的关注和重视。美国数学家Shapley认为投票组织中一个决策者的权力大小就是其成为关键加入者的概率,决策者能够通过自己的加入使得一个原本失败的联盟转变为成功,该决策者就是关键加入者 [1] 。1965年,法律专家班扎夫引入“摆盟”的概念并定义了一种新的权力指数——Banzhaf权力指数。“摆盟”是决策者成为“关键加入者”的联盟。Banzhaf权力指数为决策者拥有的摆盟数除以所有决策者摆盟数之和 [2] 。
Bilbao分析了欧盟扩大到27个国家后的决策规则下各成员国的Banzhaf权力指数 [3] 。赵昌文和庄道军通过Banzhaf指标模型,对我国上市公司的有效控制力展开了研究调查与实证分析,并得出了上市公司的绝对合理控股比率 [4] 。逢淑梅和易建新用Banzhaf指数来研究国有股减持问题,用几个具体例子来说明,若要保持第一大股东的相对控股地位,第一大股东所持有股票的数量可以远远小于上市公司股票发行总量的 [5] 。王华和汪贤裕通过Banzhaf势指标的定量分析,研究了经营性国有资产怎样达到对公共项目的相对控制问题 [6] 。姚大庆使用Banzhaf指数和Coleman指数计算了国际货币基金组织(IMF)执行董事会成员的投票权,结果显示IMF的投票规则增强了美国的控制力 [7] 。
综上所述,目前Banzhaf权力指数的研究只针对局中人完全参与到一个特定的联盟之中,即每个局中人要么参加某个联盟,要么不参加某个联盟,不存在局中人以一定的参与率或参与程度参加某个联盟。本文旨在研究局中人的参与程度对局中人投票权的影响,并提出了一种基于模糊数概念的股权模糊延拓方法。本文的结构如下:第二节将介绍研究所需的基础知识;第三节将用Tsurumi的方法和模糊数学相关理论,重新定义决策者模糊股权函数,并构造了模糊Banzhaf权力指数;第四节运用模糊Banzhaf权力指数对合伙人集团和各股东的投票权进行计算和分析。
2. 预备知识
Banzhaf权力指数用来衡量一个决策者的权力大小,其数学表达式如下:
定义2.1 [2] 决策者i的Banzhaf权力指数为
,
,
其中,
表示决策者i成为“关键加入者”的次数;
表示所有决策者成为“关键加入者”的次数之和;
表示N中所有包含决策者i的获胜联盟子集;v代表一个联盟的效益值,若该联盟为获胜联盟则v等于1,否则为0,
表示决策者i背离联盟
后
的效益值,若此时
仍为获胜联盟则
等于1,否则
等于0。
模糊数是由L.A.Zadeh于1965年提出的,他将元素对集合的隶属程度用
区间中的一个数表示,如下:
定义2.2 [8] 设论域为X,x为X中的元素,对于任意的
,给定如下的映射:
,
,
则称如下的“序偶”组成的集合
,
为X的模糊集合,称
为A的隶属函数。对某个具体的x而言,
称为x对A的隶属度,表示人们认识客观事物所赋予的元素x隶属于集合A的程度。
所有经典合作博弈的集合记为
,所有模糊合作博弈的集合记为
。
以下定义由Tsurumi给出。
定义2.3 [9] 给定联盟
,令
,
为
中元素的个数,将
中的元素按照非减序列排列为
,则具有实值模糊联盟合作对策的支付函数
是模糊联盟
到实数
的一个映射,即
,具有形式
,
其中,
;
;
表示参与程度
的所有局中人组成的清晰联盟,
为清晰联盟合作对策的支付函数,即
。
阿里合伙人模式下,候选人必须获得合伙人内部半数以上支持,以及股东大会表决时多数通过方能成功当选为董事。假设合伙人集团有n个成员,股东大会有m个主要股东,可将合伙人集团和股东大会分别看作两个加权投票博弈
和
:
,
其中,
是股东i拥有的股权。获胜联盟
。
定义2.4 [10] 设v是一个简单博弈,S为一个决策者i参加的联盟。如果S胜利,而
失利,则S称为决策者i的一个摆盟。
1) 每位合伙人的摆盟数
;
表示小于等于n/2的最大正整数,
是
中所有获胜联盟的集合,
是集合
中含有的元素个数。
2) 股东j的摆盟数
:
,
。
是博弈
中股东j所有摆盟的集合。
合伙人集团的Banzhaf权力指数:
合伙人集团内部每位新的合伙人都是由原合伙人集团投票表决产生,因此合伙人集团是一个利益共同体,可以将他们看作一个意见一致的整体,计算整个合伙人集团的Banzhaf权力指数。
,
其中,
为集团摆盟比,即所有股东的摆盟数总和除以合伙人集团的摆盟数。合伙人集团的投票权与集团摆盟比成反比。
每位股东的Banzhaf权力指数:
,
其中,
为股东i的股东大会相对摆盟比,即博弈
中股东i的摆盟数除以所有股东的摆盟总数。
在经典合作博弈中,设
为全体局中人集合,N的全部子集组成的集合为
,
中的任意元素W为经典合作博弈中的联盟。
由于股份
,
,也就是说联盟W的股份为W中所有局中人的股份之和,所以联盟越大,
的值越大,如下。
性质2.5
,若
,则
.
当股份
大于50%时,联盟W才能成为获胜联盟。此时联盟W的效益值为1,如下
性质2.6 若
,则
;否则
.
3. 模糊Banzhaf权力指数的应用
为了研究局中人的参与程度对局中人投票权的影响,本节将用Tsurumi的方法和模糊数学相关理论,重新定义决策者模糊股权函数。
若决策者能够通过自己的加入使得一个原本失败的联盟转变为成功,该决策者就是“关键加入者”,即
且
,
,
。令
,如果
,
,那么局中人i不是联盟W的“关键加入者”。
在模糊合作博弈中,设
为全体局中人集合,N的全部模糊子集组成的集合为
,
中的任意元素K为模糊联盟,用模糊集合的特征函数表示联盟K为
,
其中,
是模糊集合K的特征函数,它被定义为
,被表示为模糊联盟K中的局中人i的成员等级,
。
利用定义2.3 [9] ,可以重新定义模糊联盟的股权函数
,
,也就是将Tsurumi定义的模糊博弈
上的支付函数
直接改为股权函数
,用于计算Banzhaf权力指数,如下。
定义3.1 给定模糊博弈
,模糊联盟
,令
,
为
中元素的个数,将
中的元素按照非减序列排列为
,则存在股权函数
,具有形式
其中,
;
表示参与程度
的所有局中人组成的清晰联盟。
这样定义的股权函数
具有单调性,如下。
引理3.2 对于模糊联盟合作对策
,股权函数
满足
,
且
.
也就是说,
上的股权函数
关于局中人参与联盟的程度单调非减。
证明:从
和
的定义知道,若
,则
。再由性质2.5得到,
。最后由股权函数的定义得到,
,
.
引理3.3 对于模糊联盟合作对策
,
当且仅当
,
。
证明:将
和
中的全部元素重新排列为
,其中
,
是
中元素的个数。根据股权函数的定义,
。因此若
,则
。由于
,所以有
。
可以应用引理3.3得到,如果
,
,
那么局中人i不是模糊联盟K的“关键加入者”。
利用文献 [11] 中的定义4.2.5,可以重新定义具有区间值的模糊联盟股权函数
,
,同定义3.1的方法一样,如下。
定义3.4在模糊合作博弈中,令每个决策者i的模糊联盟程度为
,其中
,
为
中元素的个数,
为
中元素的个数,将
和
中的元素按照非减序列分别排列为
,
,则定义具有区间值的模糊联盟股权函数
为
,
其中,
;
;
。
推论3.5 在模糊合作博弈中,满足
,即
和
可以构成区间
。
证明:由引理3.2可知,
上的股权函数
关于局中人参与联盟的程度单调非减。对于
,那么有
。
利用模糊联盟股权函数
计算模糊Banzhaf权力指数的方法和原来计算Banzhaf权力指数的方法一样,这里将股份换成了股权函数,如果股权函数值大于50%,那么对应的联盟为获胜联盟。这样计算的模糊Banzhaf权力指数具有单调性,如下。
引理3.6 对于决策者i,当
时,其模糊Banzhaf权力指数满足
.
也就是说,
上的模糊Banzhaf权力指数关于局中人参与联盟的程度单调非减。
证明:由推论3.5可知,对于决策者i,当
时,有
。根据性质2.6,
越大,就越有可能超过50%,使得联盟K成为获胜联盟。因此
,即局中人i的参与程度越高,N中所有包含决策者i的获胜联盟子集就越多,局中人i成为“关键加入者”的次数
也会随之增大,即
。
推论3.7 在模糊合作博弈中,模糊Banzhaf权力指数为
.
证明:由引理3.6可知,
上的模糊Banzhaf权力指数关于局中人参与联盟的程度单调非减。对于
,那么有
。
上的模糊Banzhaf权力指数关于局中人参与联盟的程度单调非减的具体例子,如下所示。
例1假设一个公司有4个股东,他们持有股份分别为
,参与率分别为
。由定义3.2可知,当
时,只有一个获胜联盟,因此股东1的模糊Banzhaf权力指数
;当
时,获胜联盟有
和
,因此股东1的模糊Banzhaf权力指数
;当
时,获胜联盟有
,
和
,因此股东1的模糊Banzhaf权力指数
;当
时,获胜联盟有
,
,
和
,因此股东1的模糊Banzhaf权力指数
;当
时,获胜联盟有
,
,
,
和
,因此股东1的模糊Banzhaf权力指数
;当
时,获胜联盟有
,
,
,
,
和
,因此股东1的模糊Banzhaf权力指数
。由上面结果可以看出,
上股东1的模糊Banzhaf权力指数关于局中人参与联盟的程度单调非减,如图1所示:
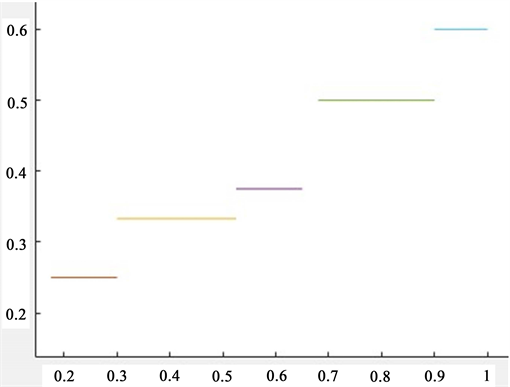
Figure 1. The fuzzy Banzhaf power index is monotonically non-decreasing about the degree of player 1 participating in the alliance
图1. 模糊Banzhaf权力指数关于局中人1参与联盟的程度单调非减
推论3.8平行投票选择结构二元选择条件下,模糊Banzhaf权力指数为
。
证明方法同上。
把模糊Banzhaf权力指数应用到定义2.4中,可以得到以下结论。
推论3.9 给定模糊博弈
,S为一个决策者i参加的模糊联盟。如果S胜利,而
失利,则S称为决策者i的一个摆盟。每位合伙人参与联盟的程度为
。
1) 每位合伙人的摆盟数
:
;每位合伙人的模糊Banzhaf权力指数为
;
2) 股东j的摆盟数
:
;每个股东的模糊Banzhaf权力指数为
,
其中,
,
,
是股东大会中股东j所有摆盟的集合。从公式中可以看出每位合伙人的联盟态度并不会影响Banzhaf权力指数。
4. 案例分析
根据阿里巴巴公司2017年公布的数据,阿里巴巴的股权结构如下表1所示:

Table 1. Alibaba equity structure table
表1. 阿里巴巴股权结构表
软银、雅虎、马云、蔡崇信等分别为阿里巴巴公司的前四位股东,而其余股份则被数量庞大的散户所占有,并无法对选举结果形成重要影响,所以在企业投票或表决等一般事务之时,仅顾及前四位股东的影响力。已知的选出董事方式是遵守简单多数准则(>50%),且当前合作组织共有36位合伙人。股东软银、雅虎、马云、蔡崇信(这里分别令为1, 2, 3, 4)分别以
,
,
,
的参与率参与该合作项目,则由定义3.4知
,
股东1,2,3,4组成联盟的预期股权为(这里只写(>50%)的股权):
;
.
而
;
.
股权函数为
.
情况一:当
,
时,胜利联盟只有
,且任何股东都是
的“关键加入者”。
,
,由推论3.14可知,
,
,
,
.
情况二:当
时,
只能取
,胜利联盟就有
,除了股东4,任何股东都是
的“关键加入者”,
,
,
。同上
,
,
,
;
,
。
根据情况一,每个股东的权力指数都是相同的,那么每个股东的投票权都是一样的,股东大会他们四人联合的获胜联盟,他们四人都是关键加入者,任何一人的离开都会使联盟由成功变为失败。合伙人的模糊Banzhaf权力指数为53.72%,超过了股东的模糊权力指数,可见合伙人控制着公司的大部分投票权。
根据情况二,股东1,2,3的权力指数都是相同的,那么他们的投票权都是一样的,股东大会他们三人联合的获胜联盟,他们三人都是关键加入者,任何一个人的离开都会使联盟由成功变为失败。合伙人的模糊Banzhaf权力指数为64.6%,超过了股东的模糊权力指数,可见合伙人控制者公司的大部分投票权。
将情况一与情况二做比较,发现随着
的增大,合伙人的模糊Banzhaf权力指数变大。与原合伙人集团和股东大会的加权投票博弈系统 [10] 相比,本文多了一种新的结果,即情况一。在情况一中,合伙人与股东大会是独立的两个实体,合伙人控制着公司的大部分投票权,股东的联盟程度较低影响了股东的权力指数,导致股东的投票权变小。这表明股东的联盟程度影响了股东在公司决策中的影响力。
因此,本文的优势在于将股东的联盟程度对股东投票权的影响进行了分析,揭示了股东的联盟程度对股东投票权的重要性:每个股东的模糊Banzhaf权力指数关于局中人参与联盟的程度单调非减。这一新的结果丰富了以前的研究内容,为我们更好地理解公司治理结构和决策过程提供了新的视角。
5. 结论
为研究局中人的联盟程度对局中人投票权的影响,本文使用模糊数的概念对股权进行模糊延拓,以更好地反映现实情况中的不确定性和模糊性。通过应用Tsurumi的方法,能够更好地量化决策者的投票权,并获得其模糊股权函数。与经典的Banzhaf权力指数相比,本文提出的方法将股权用股权函数来表示,研究了股东的联盟程度对股东在公司决策中的影响力,更加贴近现实。
运用模糊Banzhaf权力指数计算了合伙人集团和各股东的投票权并得到以下结论:每个股东的模糊Banzhaf权力指数关于局中人参与联盟的程度单调非减,证明了所提出的方法的可行性。
致谢
感谢审稿人对原稿提出的宝贵意见和建议。
基金项目
本文由贵州省教育厅科学基金(黔科合KY字[2021]088号,黔科合KY字[2022]301)、贵州省师范学院博士基金(No. 2021BS005)资助。
NOTES
*通讯作者。