1. 引言
玻璃制品是早期贸易往来的宝贵物证,我国古代玻璃吸收其技术后在本土就地取材制作,因此与外来的玻璃制品外观相似,但化学成分却不相同。玻璃一般是用多种无机矿物(如石英砂、硼砂、硼酸、重晶石、碳酸钡、石灰石、长石、纯碱等)为主要原料,另外加入少量辅助原料制成的。它的主要成分为二氧化硅和其他氧化物。石英主要也是物理风化和化学风化,这取决于石英所处的环境,寒冷干燥的环境容易发生物理风化,高温潮湿的环境容易发生化学风化。而古代玻璃极易受环境的影响而风化。在风化过程中,内部元素与环境元素进行大量交换,导致其成分比例发生变化,从而影响对其玻璃类型的正确判断。在众多方法中,我们采用斯皮尔曼系数法对表面风化与其玻璃类型、纹饰和颜色的关系进行分析,Spearman秩相关系数 [1] 是一个非参数性质(与分布无关)的秩统计参数,由Spearman在1904年提出,用来度量两个变量之间联系的强弱。基于主成分分析法和聚类分析法对每个类别进行亚分类,主成分分析 [2] (Principal Component Analysis, PCA),最早是由K·皮尔森(Karl Pearson)对非随机变量引入的一种统计方法,而后H. 霍特林将此方法推广到随机向量的情形。聚类分析的早期研究始于60年前——K-means算法的出现,它最初在1955年由Steinhaus提出,随后Stuart Lloyd在1957年提出K-均值聚类算法。K-means算法是一种基于距离的典型的聚类算法,采用以距离作为相似性的评价指标,认为两个对象的距离越近,其相似度就越大。通过K-means算法 [3] 实验项目comb叙述K-means算法的实现,并进行了结果分析。这是一种用于推荐系统的早期技术,可以将用户分成不同的组别以便针对性地推荐,因此聚类分析被划分至应用阶段。关于BP神经网络分析对玻璃类型鉴定,BP (back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,是应用最广泛的神经网络模型之一。BP (back propagation)神经网络 [4] 首先获得大量相关的评估指标,通过主成分分析法(PCA)剔除不重要指标。对于指标赋权,先用基于蒙特卡罗的层次分析法(AHP-MCA)初步给指标赋权,由于此法具有一定主观性,因此进一步采用BP神经网络算法对所赋权重进行训练调节,过程中需要一个标准比对物,最终得到符合实际结果。
2. 对表面风化与其玻璃类型、纹饰和颜色的关系进行分析
由于原始数据有缺失,因此将定类数据转化成定量数据后用同组的平均值进行填充,再将获得的平均值转化成对应的定类数据 [5] 。当两个变量之间的相关系数完全相同,斯皮尔曼相关系数就是±1。
利用(1) (2)式可计算得各变量之间的斯皮尔曼系数,结果如表1所示。
(1)
其中n为样本容量,α为相关系数,
分别是类型、颜色、表面风化的其中任意两个值。将两个变量的对应元素相减得到一个差值a,进一步将上面的公式进行优化:
(2)
利用斯皮尔曼相关系数分析,做出风化对玻璃类型、纹饰、颜色之间的关系图,见表1。
注:***、**、*分别代表1%、5%、10%的显著性水平。
同时对类型、颜色、纹饰和表面风化两两之间进行计算,判断两个变量之间是否存在显著性和相关性并检验(P < 0.05)。
根据风化对玻璃类型、纹饰、颜色之间的影响,做出图1和图2 。
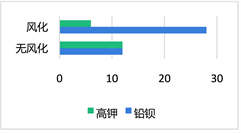
Figure 1. The relationship between weathering and glass type
图1. 表面有无风化与玻璃类型的关系
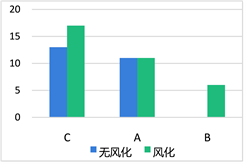
Figure 2. The relationship between weathering and glass ornamentation
图2. 表面有无风化与玻璃纹饰的关系
从图1中可以看出,风化的玻璃中铅钡型玻璃占比比高钾型玻璃多,无风化的玻璃中高钾型玻璃和铅钡型玻璃占比一样多从图2中可以看出,风化的玻璃中C类到A类到B类纹饰呈下降趋势,无风化的玻璃中也是C类纹饰占比大,A类和C类纹饰占比相近,两种类型都是B类纹饰少,所以大致看出有无风化与纹饰的相关性不大。
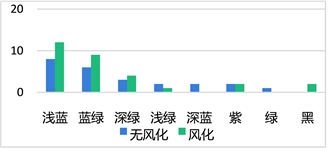
Figure 3. The relationship between surface weathering and glass color
图3. 表面有无风化与玻璃颜色的关系
从图3中可以看出,只有风化玻璃有黑色,只有无风化玻璃有深蓝色和绿色。除以上的颜色外,浅蓝色和蓝绿色玻璃在风化玻璃中的占比大于在无风化玻璃中的占比。
通过对斯皮尔曼相关系数分析可知,古玻璃类型、颜色、纹饰、表面风化之间两两对比发现对于表面风化来说,与其他因素相比,类型与表面风化呈显著性,表明它们之间有相关性。从柱状图中分析,也可以看出与斯皮尔曼系数结论相近的体现。
3. 基于主成分分析法和聚类分析法对每个类别进行亚分类
由上节的分析可知不同类型的古代化学玻璃与其表面风化之间存在显著关系,因此本节以此为出发点找到不同玻璃类型的主要影响因素,从而得知类型的分类规律。再对两个类型的化学成分进行主成分分析,获得主成分总得分计算模型,用聚类分析模型对它们的化学成分的主成分得分进行亚分类,得出分类结果。对原数据进行波动处理再用原方法计算主成分得分,观察与原数据的波动大小进行敏感性分析。
3.1. 对高钾每个类别进行亚分类
主成分分析法主要运用降维思路将多维的多指标通过降维来获得一个可以体现整体的综合指标,其本质是通过变量之间的相关性和权重寻找相应的代替指数。根据标准化后的数据集计算协方差矩阵H:
(3)
计算矩阵R的特征值
及对应的特征向量
中
,unj表示第j个特征向量的第n个分量;由特征向量组成n个新的指标变量:
(4)
式中,y1是主成分1,y2,是主成分2,计算各主成分yj贡献率
即
的贡献率αp。
(5)
(6)
基于主成分分析法,计算得出以下成分矩阵表,见表2。
上表为成分矩阵表,意在说明各个成分的所包含的因子得分系数(主成分载荷),用于计算出成分得分,得出因子公式,其计算公式为:线性组合系数 × (方差解释率/累积方差解释率),最后将其归一化即为因子权重得分,见表3。
由上表主成分权重分析得出模型的公式:
(ai为主成分1里各成分对应的主成分载荷,bi为各成分对应的值)。
(xj为主成分2里各成分对应的主成分载荷,yj为各成分对应的值)。
由以上可以得到:
,具体得分见表4。

Table 4. Cultural relic principal component score
表4. 文物主成分得分
基于上述主成分总得分,进行聚类分析。首先,从数据组中任意选取n个初始量作为聚类中心,计算其他数据与该中心的欧氏距离,找出与该中心最近的中心pj,然后将合适的数据分到中心pj的组中,接着计算组中数据的平均值来寻找更为准确的聚类中心,直到中心不再变化。
空间中数据对象与聚类中心间的欧式距离计算公式为:
(7)
其中,y为计算的原数据,pj为第j个聚类中心,n为原数据的维度,ya,cjt为对应中心中第a个属性,整个数据集的误差平方和SSE计算公式为:
(8)
其中,SSE的大小表示聚类结果的好坏,m为组的个数。
具体结果见表5。
注:***、**、*分别代表1%、5%、10%的显著性水平。
方差分析的结果显示:
对于变量主成分得分在进行聚类分析时存在显著差异,证明可以进行聚类分析,并且将主成分得分分为三大类,结果见表6。
通过以上分类数据,对高钾类文物进行以下亚分类,见表7:

Table 7. High potassium type glass subclassification table
表7. 高钾类型玻璃亚分类表
3.2. 对铅钡每个类别进行亚分类
同理通过高钾亚分类方法,得到以下结果,见表8:
由上表主成分权重分析得出模型的公式:
(ai为主成分1里各成分对应的主成分载荷,bi为各成分对应的值)。
(xj为主成分2里各成分对应的主成分载荷,yj为各成分对应的值)。
由以上可以得到:
,具体结果见表9:

Table 9. Principal component scores of artifacts
表9. 文物的主成分得分
对于变量主成分得分在进行聚类分析时存在显著差异,证明可以进行聚类分析,并且将主成分得分分为三大类,结果见表10。
通过以上分类数据,对铅钡类文物进行以下亚分类,见表11:

Table 11. Lead barium type glass sub classification table
表11. 铅钡类型玻璃亚分类表
4. 基于BP神经网络分析对玻璃类型鉴定
通过上节对古代玻璃的主成分分析和亚分类,找到对于玻璃分类影响较大的元素,再依据基于BP神经网络建立古代玻璃分类的预测模型。以主要化学成分氧化铅、氧化钡、氧化钾、氧化镁,以这五个元素为自变量,以类型为变量对题目所给的表单2的数据进行处理,再根据表单3中的化学成分进行模型预测来判断其对应的玻璃类型。通过对原数据进行波动处理再用训练后的模型进行计算,通过与原数据的高钾铅钡指数对比进行敏感性分析。
关系层的输出值设为Fj,输出层的输出量设为Ak,系统的激励函数设为P,学习速度设为σ,则其三个层之间有如下数学关系:
(9)
设系统期望的输出为Tk,所以用实际的输出与期望的方差来表示差异性,具体关系表达式如下:
(10)
并令
,利用梯度下降原理,则系统权值和偏置的更新公式如下:
(11)
(12)
由题干中的描述可得玻璃的主要成分是(SO2),而铅钡玻璃与高钾玻璃对比有明显差别的化学成分有(Al2O3),(BaO),(K2O)和(MgO)。所以以这五个元素为自变量,以类型为变量来进行BP神经网络分析,并对表单3中的数据进行类型判别。
通过SPSS [5] 软件对表单三中的数据对应的类型进行判别,见表12:
5. 古代玻璃化学成分之间的关联关系,以及不同类别的差异性比较
5.1. 基于灰色关联模型对高钾化学成分之间的关联关系分析
基于上节对于古代化学玻璃类型的预测模型,为了进一步找出主要影响因素。根据所给数据筛选出高钾和铅钡玻璃的数据分别对两种类型的玻璃进行分析,通过各种化学成分的关联系数算出两种类型中不同化学元素的关联度排序,同时比较两种类型玻璃相同化学成分的关联度排序得出差异性。
步骤1:把玻璃类型转化成定量数据后作为母数列,化学成分作为特殊数列。
比较序列为:
(13)
母序列(即评价标准)为:
(14)
步骤2:为使最后的结果更加真实,排除单位,数量级等差别对最后结果的影响,减少大偏差现象发生的可能性,对指标进行量纲一体化处理。
步骤3:计算关联系数。由下式分别计算每个比较序列与参考序列对应元素的关联系数:
(15)
(16)
(17)
(18)
ρ1为分辨系数,在(0,1)内取值,通常取0.5,分辨系数与系数间的差异性成负相关。
步骤4:计算关联度。
将各指标与母序列的相对应的分辨系数通过求加权平均值的方法获得单一的量,将各指标的关联度进行排序用来体现各指标与母序列的关系。
关联度计算公式:
(19)
具体灰色关联系数见表13。
从上表可知,针对14个评价项(SiO2)、(Na2O)、(SO2)、(SnO2)、(K2O)、(SrO)、(P2O5)、(BaO)、(PbO)、(CuO)、(CaO)等以及16项数据进行灰色关联度分析,关联系数代表化学成分与高钾玻璃的相关性大小。
灰色关联度排名见表14。
通过对灰色关联系数求平均值获得关联度并对关联度进行排名,区分出个化学成分对于高钾类型的关联关系的高低。
5.2. 铅钡玻璃化学成分之间的关联关系,以及不同类别的差异性比较

Table 15. Lead barium grey correlation coefficient
表15. 铅钡灰色关联系数
从上表可知(表15),针对14个评价项(SiO2)、(Na2O)、(K2O)、(SO2)、(SnO2)、(P2O5)、(SrO)、(BaO)、(CuO)、(PbO)、(Fe2O3)等以及40项数据进行灰色关联度分析,关联系数代表化学成分与铅钡玻璃的相关性大小。
灰色关联度排名见表16。

Table 16. Lead barium gray correlation degree
表16. 铅钡灰色关联度
通过对灰色关联系数求平均值获得关联度并对关联度进行排名,区分出个化学成分对于铅钡类型的关联关系的高低。
根据以上表格做出如下折线图图4:

Figure 4. Comparison of correlation degree of chemical elements between high potassium and lead barium glass
图4. 高钾和铅钡玻璃各化学元素关联度对比
6. 主要结论
通过本文建立的预测模型可以在后期预测的时候直接代入所需的化学元素值来对古代化学玻璃的类型进行预测。如果无法探测本文中所给的元素值,可以依照第五节中不同类型化学玻璃和其灰色关联元素的排行选择易于探测的并关联度大的元素,再依照第四节的BP神经网络建立新的预测模型来达到预测的效果。后期如果还要对古代玻璃进行除了高钾玻璃和铅钡玻璃外的细分,可以通过第三节的主成分分析和依据主成分分析的亚分类进行。
基金项目
桂林电子科技大学信息科技学院2020年科研项目(XJ202025);桂林信息科技学院2022年科研项目(XJ202218)。
NOTES
*通讯作者。