1. 引言
近年来,为深入贯彻习总书记的重要讲话精神,将教书育人的内涵落实在课堂教学中,培育符合中国特色社会主义的道德观、人生观、世界观和价值观要求的高素质人才,各高校掀起课程思政教育改革的热潮。课程思政是国家对高等教育提出的新要求,也是高校实现高质量发展的必然需求 [1] 。对课程思政的相关研究主要包括:课程思政的内涵研究、课程思政元素的挖掘、课程中如何融入思政元素以及实施课程思政的策略等 [2] [3] [4] 。课程思政主要形式是将思想政治教育元素,包括思想政治教育的理论知识、价值理念以及精神追求等融入到各门课程中去,潜移默化地对学生的思想意识、行为举止产生影响 [5] 。课程思政实质是一种课程观,不是增开一门课,也不是增设一项活动,而是将高校思想政治教育融入课程教学和改革的各环节、各方面,实现立德树人润物无声,围绕“知识传授与价值引领相结合”的课程目标,强化显性思政,细化隐性思政,构建全课程育人格局 [6] 。教书育人,是教师的基本职责,课堂是教师的主战场,教师作为课堂教学的负责人,要提高专业能力和素质水平,增强改革意识,积极主动地投入到课程思政教育教学改革中。
2. 高等数学教学中课程思政现状
高等数学课程是面向本科一年级、学生最先接触的和学时相对较长的一门重要的公共基础课,具有严密的逻辑性、高度的抽象性和广泛的应用性的特点,是最让学生头疼,挂科率高的一门课程。经过三年紧张的高中生活,学生习惯了填鸭式的教学方法和教师主导下的应试教育,进入大学后往往不能适应高等数学中的思维方法、课堂节奏和教学模式。个别学生脱离了父母的管教后自控力差从而放飞自我,再加上学生的世界观、人生观和价值观没有成型,思想和观念不成熟,很容易受到外界的干扰和影响。
高等数学的课程目标通常专注于学生的分析和解决问题的能力、抽象思维和逻辑思维能力的培养,对学生的道德品质和科学素养的关注与培养不足。很多教师习惯了传统的教学方式,对课程思政的概念理解不清、对课程的育人功能认识不足、对课程思政元素挖掘不够深入、不知如何进行思政教育、没有时间和精力进行思政改革、缺乏动力,甚至存在抵触的思想。
高等数学课程蕴含着丰富的科学思想、数学精神和方法论,课堂教学融入思政教育,不仅能够使学生尽快适应大学生活,端正学习态度,也能够对学生的世界观、价值观及精神品格的形成产生巨大的影响,更能够提升教师的专业水平,扭转传统的教学思维。所以,教师应深入探索、研究和总结课程内容所涉及的数学思想与精神,与实际问题相结合,深度挖掘设计高等数学课程思政案例,积极进行思政教育改革,利用好高等数学课堂教学这个主渠道,给抽象的数学课注入更多的活力与养分。
3. 高等数学教学中课程思政案例探析
课程思政案例要紧扣时代发展主题,与社会和生活紧密结合,贴近学生实际。在课堂教学中,我们主要从数学史、国家高科技工程、数学家轶事和生活中挖掘高等数学课程思政元素,设计思政教学案例,在课堂教学中取得了较好的教学效果。
3.1. 从数学史中挖掘课程思政元素
数学史不仅是描述数学的历史,追溯数学内容、方法、思想的演变和发展过程,也是通过数学的发展规律,阐释其给人类文明带来的巨大影响。因此,数学史具有丰富的人文和教育价值。
案例1 常量到变量
中小学阶段的初等数学是常量数学,高等数学是变量数学。由常量到变量,由静态到动态,由已知到未知,体现了数学的内在发展规律,更体现了人类文明发展所遵循的基本法则。在高等数学第一节课中,通过常量到变量及变速运动、变力做功或曲边形的面积等实例的讲解,让学生初步认识高等数学,了解数学中的“变”与“不变”及实际中的简单数学问题,清楚变量数学中的“变”(未知,不确定)是用常量数学中的“不变”(已知)来解决的。
案例解析:世界是千变万化的,只有夯实基础,不断提高,适应环境,调整策略,才能以不变应万变。只有善于发现问题并解决问题,不断求真探索、改革创新,才能建立起变量数学的高楼大厦,推动数学的发展和人类文明的进步。
案例2 危机与转机
牛顿和莱布尼茨发明了微积分,却遭到一些人的强烈反对和攻击。英国大主教贝克莱提出了悖论公式:
(1)
即在求导时,
作为分母时不为0,但是在最后又等于0,这是矛盾的。这种矛盾困扰了数学家一百多年,由此产生了第二次数学危机。直到法国数学家柯西用极限定义了无穷小量,才彻底解决了这个问题。
案例解析:由危机到转机虽然持续时间有点长,但只要坚持不懈,不断地努力、奋进和积累,就能转危为安,迎来生机。而无穷小量这个“小人物”一点也不小,它制造了危机,也化解了危机。让学生知道,任何时候都不能小瞧或忽略这样的“小人物”,要具有一丝不苟,严谨细致的学习和工作态度。
3.2. 从高科技工程中挖掘课程思政元素
数学是工具,为社会生产与生活服务。从中国天眼到国产大型客机,从青藏铁路到天宫一号,每个国家高科技工程都与数学息息相关。
案例3 中国天眼与平面
中国天眼FAST是目前世界上最大、最灵敏的单口径射电望远镜,代表着我国高科技发展水平。FAST的反射面是直径为500米的球面(球面方程为:
),由4450块三角形平面面板组成。看似光滑的球面望远镜,却由一个个大小不同的三角形平面反射面板拼装而成。可见,平面看起来简单,构造的东西却不简单,它承载着人类探索宇宙的科技使命。
案例解析:从天眼的选址、三角形反射面板的选择及重量的测算,到望远镜的拼装与搭建、复杂的综合布线工程和数据处理系统,无不体现着科学家和工程师们锲而不舍,精益求精的工匠精神。复杂的系统工程背后,更需要扎实的理论知识做支撑。鼓励学生学好基础理论知识,提升专业文化水平,为国家的科技发展做出贡献。
案例4 国产大型客机与微分方程
2023年5月,国产C919大型客机完成商业首飞,正式进入民航市场,开启常态化商业运行。飞行器是一个复杂的动力学系统,其飞行特性可用微分方程来描述。如某飞行器纵向模型就是关于速度V、攻角
、俯仰角速度q、俯仰角
、高度h和弹性模态
的微分方程:
(2)
飞行器动力学模型呈现强非线性和强耦合性的特性。要想建立能够清晰描述飞行器运动规律,体现真实飞行物理特性的模型,不能一蹴而就,而是需要多部门多学科综合建模,更需要长时间的积累、研究、设计、模拟和试验才能成功。
案例解析:飞机从蓝图到飞上蓝天,背后是成千上万名科技工作者和工程师们付出的辛勤汗水。只有通过多部门团队协作,齐心协力,坚持不懈,才能攻坚克难,实现目标。鼓励学生组建学习团队,积极参加课题或比赛,提高团队合作能力和组织能力,共同进步。同时树立信心,增强民族自豪感,做新时代的有志青年。
3.3. 从数学家轶事中挖掘课程思政元素
高等数学中很多定理或定义都是以数学家名字命名的。这些名字的背后都是数学家成长、教育、励志和成才的故事,蕴含着丰富的课程思政元素。
案例5 洛必达与洛必达法则
公元17世纪,酷爱数学的法国贵族洛必达用财物换取了其生活困难的老师约翰·伯努利的学术论文,这篇论文的内容就是影响数学界的洛必达法则。洛必达通过整理换来的和自己研究出来的成果,编写出世界上第一本微积分教材,为数学的发展做出了重要的贡献。在那个年代,物物交换是正常的行为,但是在现代社会,剽窃、抄袭或买卖他人成果都是不可取的。
案例解析:只有通过自己的努力,收获的成果才是货真价实的。鼓励学生要实事求是,诚实守信,求真务实,具有科学探索精神,独立思考和判断的能力,追求真理,实现个人抱负。
案例6 牛顿与鼠疫
公元1665年,剑桥大学因为鼠疫传播而关闭,牛顿回到家乡进行自我隔离。在避疫的两年时间里,牛顿停课不停学,潜心研究和累积,万有引力、光学分析和微积分的思想开始孕育,在数学、光学和力学等领域取得了重要突破。疫情结束,牛顿回到剑桥半年后便被评为院士。
案例解析:通过牛顿的故事,引导学生要以科学的态度和良好的心态面对困难,绝不能“躺平”和“摆烂”,要脚踏实地,潜心学习,磨练意志,厚积薄发,定能取得成功。
3.4. 从生活中挖掘课程思政元素
从吃饭的锅碗瓢盆,出行的交通工具,到路边的风景,形态各异的建筑,数学蕴藏在生活的每个角落。恰当地将身边的生活案例融入到高等数学课堂中,能起到很好的教学效果,使枯燥乏味的数学知识变得生动有趣,吸引学生的注意力,调动学生学习的主动性和积极性,同时还能进行思政教育。
案例7 生活与数学
1) 奔流不息的长江与黄河可以引出函数的连续性。广州塔“小蛮腰”、国家大剧院和速滑馆等建筑都是二次曲面。天宫一号的运行轨迹和城市建筑的轮廓是空间曲线。高速铁路的瞬时速度和导数的定义有关。大型客机飞行中机身的弹性振动可以用偏导数描述。计算学校所在的天津滨海新区的面积可以引出定积分的概念。
案例解析:引导学生积极发现和感受身边的数学和数学的美,要用学到的知识去创造美,激发学生的爱国热情,增进学生对求学城市的了解和认同,感受城市发展的日新月异,感受国家的发展与进步,增强民族自豪感、自信心和凝聚力。
2) 刘徽“割圆术”和《庄子·天下篇》中“一尺之锤,日取其半,万世不竭”中蕴含数列极限的思想。李白的《送孟浩然之广陵》中“孤帆远影碧空尽,唯见长江天际流”中含有无穷小量。苏轼的《题西林壁》中“横看成岭侧成峰,远近高低各不同”体现了函数的极值和最值。叶绍翁的《游园不值》中“春色满园关不住,一枝红杏出墙来”则形象地体现了无界函数的特征。
案例解析:引导学生认识数学与文学的联系,激发学生探索数学思想的兴趣,要认真学习文化知识,增强文化认同和自信,感受中国文化的博大精深及所蕴含的丰富人生哲理,丰富对中国文化历史和人类知识发展的理解。
3) 土豆佳肴的切块、切丝和切片制作可以引出三重积分的定义、“先一后二”法和“先二后一”法。传染病病毒的传播可以用微分方程描述,通过用Matlab软件求取的传染病微分模型数值解曲线图,见图1,让学生直观地看到,及时发现并隔离疑似感染者,科学防控,提高医疗卫生水平,感染者曲线就会平稳升降,从而安全度过发病高峰期。
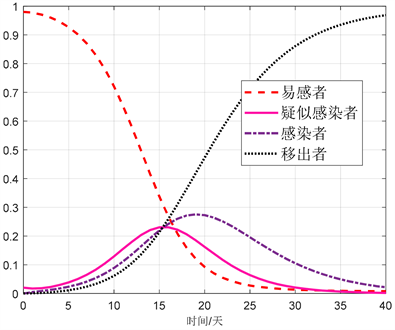
Figure 1. Numerical solution of infectious disease model
图1. 传染病模型的数值解
案例解析:引导学生要真实感受生活,关心社会动态和时事,从实际和实践中寻找真谛。鼓励学生遇到困难和危险不要惊慌,要科学应对,理性认识,服从安排,顾全大局,坚定必胜的信心,有集体观念和危机意识。
数学史、数学家故事、科技工程及我们的生活就是丰富的课程思政案例库,教师需要根据自身和学生的专业,去深度挖掘和设计适合课堂教学的案例,并恰当地融入到教学过程中,提升教学质量,实现人才培养目标。
4. 课程思政案例在高等数学课堂教学中的实践
经过凝练的课程思政案例要细化到教学大纲、讲义、教案和课件中。课堂教学需要灵活施教,通过显性与隐性思政教育结合的方式,将思政元素深度融合到教学过程中。我们在教学过程中主要采用BOPPPS教学模式,将课程思政教育贯穿到BOPPPS教学模式的六个阶段,即导入(B)、学习目标(O)、前测(P)、参与式学习(P)、后测(P)和总结(S)中 [7] 。这种教学模式能够让学生全程参与到学习过程中,有利于更好地融入课程思政案例,提高学生的学习兴趣和学习意识,及时掌握课堂内容并熟练应用,也有助于教师及时了解学生的课堂学习情况,灵活调节教学内容和进度。
在导入阶段,可以引入社会热点,历史典故或实际案例,吸引学生的注意力,提高学生的学习兴趣和探索知识的热情,进行思政教育的预热;在目标阶段,强调课程学习的知识、能力和素质目标,让学生了解知识、能力和素质目标是相统一的,有目的地参与课堂教学活动,提高教学效率;在前测阶段,针对导入阶段提出的问题,进行随机提问、抢答、讨论或测试,了解学生的预习情况,强调预习的重要性,点出问题背后的思政元素;在参与式学习阶段,通过学生自主学习、小组讨论或展示等方式进行,将讲授内容与思政案例相融合,提高学生的参与度,完成课程的学习目标;在后测阶段,了解学生对课堂内容的掌握情况,鼓励学生要善于发现身边的数学,学会从具体到抽象,从抽象再应用到实际;在总结阶段,根据学生讨论和后测的结果,总结授课内容,提炼思政主题,并对知识进行应用拓展。
课堂教学要让学生参与教学,消化知识,体会思政。以定积分的概念一节课为例,表1列出了具体的课堂教学过程及各阶段所呈现的课程思政元素。整个过程从引例的导入、知识的讲解、思政的融入到知识的拓展,从低阶到高阶,做到知识传授、思政教育和能力提升相结合。

Table 1. The concept of definite integral in classroom teaching process
表1. 定积分的概念课堂教学过程
5. 教学效果
基于BOPPPS教学模式,将课程思政元素融入到教学过程中,让学生参与其中,调动了学生学习的积极性,提高了教学效果。通过对最近教学班的问卷调查,学生对教师的授课满意度有97.81%,有90.51%的学生喜欢这种教学模式,见图2和图3。
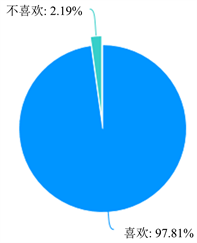
Figure 2. A survey of students’ satisfaction with teachers’ teaching
图2. 学生对教师授课的满意度调查
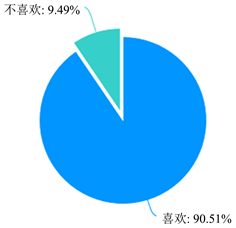
Figure 3. A survey of students’ liking for teaching modes
图3. 学生对教学模式的喜欢度调查
最近三个学年学生对教师的评教均在98分以上,见表2,说明学生对教师的整体授课情况、在高等数学的教学中使用BOPPPS教学模式和融入课程思政元素的方式是高度认可的。同时,学生学习高等数学的积极性与主动性提高,达到了教学改革的预期。

Table 2. Student evaluation scores in the past three academic years
表2. 近三个学年学生评教分数
6. 总结
针对高等数学的课程性质、课程思政的教育现状和新时代学生的特点,从数学史、国家高科技工程、数学家轶事和日常生活中挖掘典型课程思政案例,结合BOPPPS教学模式,融入到高等数学的课堂教学中。在增强高等数学课程的生动性、趣味性和参与性的同时,在课堂知识传递、日常学习和生活中,培养学生的抽象思维能力、逻辑推理能力及团队协作能力,具备解决复杂问题的综合能力和高阶思维,具有良好的道德品质和科学素养,激励学生的民族自豪感和责任感,激发学生科技报国的家国情怀和使命担当,引导学生树立正确的人生观和价值观。
基金项目
中国轻工业联合会教育工作分会/全国轻工职业教育教学指导委员会课题(QGJY2022104);中国学位与研究生教育学会面上课题(2020MSA206);中国高等教育学会高等教育科学研究规划课题(23SX0410);天津科技大学教育教学改革研究项目(KY202324)。