基于FRFT的LFM信号时延估计分析与仿真

Analysis and Simulation of LFM Signal Delay Estimation Based on FRFT

摘要: 根据分数阶傅里叶变换对线性调频(LFM)信号的独特聚集性，研究了基于分数阶傅里叶变换LFM信号时延估计，并给出了目标测距具体实现。针对接收端接收到的信号是实信号干扰时延估计的问题，采用正交下变频构造解析信号用以进行时延估计。最后通过仿真实验，验证了基于FRFT的LFM信号时延估计可行性和有效性，为目标距离检测提供了研究思路。

Abstract: Based on the unique aggregation of fractional order Fourier transform on linear frequency modula-tion (LFM) signals, the time delay estimation of LFM signals based on fractional order Fourier trans-form was studied, and the specific implementation of target ranging was provided. In response to the problem of real signal interference in time delay estimation received by the receiving end, or-thogonal down conversion is used to construct an analytical signal for time delay estimation. Finally, through simulation experiments, the feasibility and effectiveness of LFM signal delay estimation based on FRFT were verified, providing research ideas for target distance detection.

1. 引言

线性调频(linear frequency modulation, LFM)信号是自然界众多领域中都存在的一种非平稳信号 [1] ，因其具有发射功率低、作用距离远和抗多普勒频移等优点，在雷达、水下探测、UWB探测和扩频通信等领域中广泛应用 [2] 。当LFM信号用于目标距离检测时，需要对LFM信号进行时延估计，然后根据信号在介质中的传播速度得出目标距离。

传统的时延估计方法主要是互相关方法。互相关方法的原理是利用信号的互相关的峰值来对时延进行估计，但当时延小于信号时宽的情况下，相邻的两个峰值有可能会发生混叠，从而影响时延估计的精度。广义互相关方法通过对互相关函数加窗平滑，提高时延估计精度。但要求信号是平稳的，不适用于LFM信号时延估计。Wigner-Ville分布可以分析非平稳信号的频率分量随时间变化的情况，具有良好的时频聚集性，但当存在多个分量LFM信号时会有交叉项的干扰，在一定程度上影响时延估计的性能。

分数阶傅里叶变换(FRFT) [3] 是傅里叶变换的一种广义形式，其将信号变换到分数域上，可以兼顾信号时域和频域，克服了传统傅立叶变换局限性，可以用来处理和分析LFM等非平稳信号。本文根据LFM信号在特定分数域内呈能量聚集特性 [4] ，对回波信号进行FRFT变换，在分数域上寻找峰值位置偏移值，通过偏移值和时延的关系实现LFM信号的时延估计，并通过仿真给予验证。

2. 检测原理

2.1. 分数阶傅里叶变换基本原理

分数阶傅里叶变换(FRFT)是一种广义的傅里叶变换，可以将信号从时域变换到FRFT变换域中，具有分析信号局部时频特性的特点，很适合时变信号的处理和特征提取 [5] 。通常FRFT可以有若干种不同的定义方式，但每种定义彼此间都是等价的 [6] 。信号 $x\left(t\right)$ 的p阶FRFT定义如下 [7] ：

$X_p\left(u\right)=F^p\left[x\left(t\right)\right]={\displaystyle {\int }_{-\infty }^{\infty }x}\left(t\right)K_p\left(t,u\right)\text{d}t$ (1)

式(1)中，p为FRFT变换的阶次， $X_p\left(u\right)$ 为信号 $x\left(t\right)$ 经过p阶的FRFT结果， $F^P$ 为FRFT的算子， $K_p\left(t,u\right)$ 为核函数，设 $A_{\alpha }=\sqrt{1-j\cot \alpha },n=1,2,\cdots$ ，核函数表达式为：

$K_p\left(t,u\right)=\{\begin{array}{ll}{A}_{\alpha }\exp \left(j\pi \left(t^2+u^2\right)\cot \alpha -j2\pi ut\csc \alpha \right)\hfill & \alpha \ne n\pi \hfill \\ \delta \left(t-u\right)\hfill & \alpha =2n\pi \hfill \\ \delta \left(t+u\right)\hfill & \alpha =\left(2n+1\right)\pi \hfill \end{array}$ (2)

式(2)中， $\alpha =p\pi /2$ 为旋转角度， $\delta \left(t\right)$ 为单位脉冲函数。当 $p=1$ 时，有 $\alpha =\pi /2$ ，则有

$X_1\left(u\right)={\displaystyle {\int }_{-\infty }^{+\infty }x}\left(t\right){\text{e}}^{-j2\pi ut}\text{d}t$ (3)

式(3)中， $X_1\left(u\right)$ 是 $x\left(t\right)$ 传统意义的傅里叶变换，而 $\alpha =p\pi /2$ 只在三角函数的参数位置上出现。因此，当FRFT以p或 $\alpha$ 进行定义时，其参数范围是 $p\in \left(-2,2\right]$ 或 $\alpha \in \left(-\pi ,\pi \right]$ 。在 $p=1$ 即 $\alpha =\pi /2$ 的情况下，FRFT就变成传统意义上的傅里叶变换。因此，FRFT是傅里叶变换的广义形式。利用FRFT对信号进行时频分析时，时频坐标轴将旋转相应角度，如图1所示。

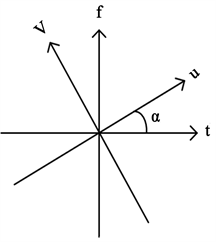
Figure 1. Time frequency coordinate rotation diagram

图1. 时频坐标旋转图

从图1中可得到FRFT另一种定义方式，即p阶傅里叶变换可以理解为信号的时频平面绕原点逆时针旋转 $\alpha$ 角度，p阶傅里叶变换的线性正则变换矩阵为：

$\left[\begin{array}{l}u\hfill \\ v\hfill \end{array}\right]=\left[\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{array}\right]\left[\begin{array}{l}t\hfill \\ f\hfill \end{array}\right]=R_{\alpha }\left[\begin{array}{l}t\hfill \\ f\hfill \end{array}\right]$ (4)

其中，u和v轴分别为旋转后的时间轴和频率轴， $R_{\alpha }$ 为旋转算子。

2.2. LFM信号在分数阶傅里叶变换域的聚焦特性

LFM信号也称为啁啾信号，是一种线性调频信号，具有抗干扰能力强、抗多普勒频偏以及高时延分辨率等特点。LFM信号是FRFT的标准正交基，根据正交基的特性，LFM信号变换到某个特定阶次的分数阶傅里叶变换域上将是一个冲击函数，产生能量聚集的特性，所以FRFT特别适合处理LFM信号 [8] 。

LFM信号的时域表达式如下所示：

$s\left(t\right)=A\exp \left(j2\pi f_{0}t+j\pi k_0{t}^2\right),0\le t\le T$ (5)

式(5)中，A为LFM信号的幅度， $f_0$ 为信号的中心频率， $k_0$ 为信号的调频斜率，T为观测时间，即信号时宽。

WVD是一种基本的二次时频分析工具 [9] ，其定义为：

$W_x\left(t,\omega \right)={\displaystyle {\int }_{-\infty }^{+\infty }{x}^{*}}\left(t-\frac{\tau }{2}\right)x\left(t+\frac{\tau }{2}\right)\exp \left(-j\omega \tau \right)\text{d}\tau$ (6)

它是双线性乘积或瞬时自相关函数 $x\left(t+\frac{\tau }{2}\right)x^{\ast }\left(t-\frac{\tau }{2}\right)$ 关于时延 $\tau$ 的FT [10] 。

根据WVD的定义可以求得LFM信号的WVD，求解过程如下：

$\begin{array}{c}{W}_x\left(t,f\right)={\displaystyle {\int }_{-\infty }^{+\infty }A}\exp [j2\pi \left[f_0\left(t+\frac{\tau }{2}\right)+\frac{k}{2}{\left(t+\frac{\tau }{2}\right)}^2\right]Aexp[-j2\pi \left(f_0\left(t-\frac{\tau }{2}\right)+\frac{k}{2}{\left(t-\frac{\tau }{2}\right)}^2\right]\exp \left(-j2\pi f\tau \right)\text{d}\tau \\ =A^2{\displaystyle {\int }_{-\infty }^{+\infty }\exp }(-j2\pi \left(f-f_0-kt\right)\tau \text{d}\tau \\ =A^2\delta \left(f-f_0-kt\right)\end{array}$ (7)

由式(7)可知，LFM信号的WVD是沿直线 $f=f_0+kt$ 分布的冲激线谱，信号的能量在这条这线上有很强的聚集特性，但是这一结论只适用于无限长的LFM信号，在实际情况中，LFM的信号长度是有限的，所以WVD呈背鳍状 [11] ，如图2所示。

Figure 2. 3D-WVD of LFM signal

图2. LFM信号的WVD三维图

由p阶傅里叶变换的线性正则变换矩阵式(4)可知，t-f平面与u-v平面的坐标变换公式为：

$\{\begin{array}{l}t=u\cos \alpha -v\sin \alpha \hfill \\ f=u\sin \alpha +v\cos \alpha \hfill \end{array}$ (8)

将式(8)带入式(7)中进行变量替换可以得到：

$f_0=u\left(\sin \alpha -k_0\cos \alpha \right)+v\left(\cos \alpha +k_0\sin \alpha \right)$ (9)

当 $\cos \alpha +k_0\sin \alpha =0$ ，即 $k_0=-\cot \alpha$ 时，LFM信号的WVD在u-v平面的表达式为:

$W_x\left(u,v\right)=A^2\delta \left(u-f_0\sin \alpha \right)$ (10)

说明LFM信号在时频平面 $\left(t\text{,}f\right)$ 的WVD是一条斜线，如果将 $\left(t\text{,}f\right)$ 坐标系进行适当的旋转形成新的 $\left(u,v\right)$ 坐标系，那么该斜线就变成一条与u轴垂直的直线，即LFM信号的分数阶傅里叶变换在 $u=f_0\sin \alpha$ 处是冲激函数。因此，对于理想状态下无限长的LFM信号，特定角度的FRFT会得到一个幅度无限大的冲激函数；对于实际中有限长度的LFM信号，其特定角度的FRFT呈现极大值，如图3所示。

2.3. 基于FRFT的LFM信号时延估计原理

线性调频信号作为发射信号的分数阶傅里叶变换测距原理，是通过对回波信号做已知角度的分数阶傅里叶变换，然后在分数域上搜索发射信号和回波信号的峰值点位置，通过峰值点位置差计算时延，最终实现估计目标距离的目的 [12] ，分数阶傅里叶变换测距原理如图4所示。

Figure 3. FRFT of LFM signal

图3. LFM信号的FRFT

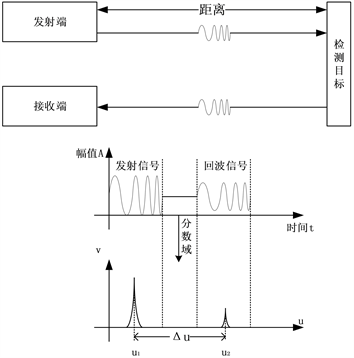
Figure 4. FRFT ranging principle diagram

图4. 分数阶傅里叶变换测距原理图

式(5)LFM信号的时延信号为：

$s_2\left(t\right)=A\exp \left[j2\pi f_0\left(t-\tau \right)+j\pi k_0{\left(t-\tau \right)}^2\right],0\le t\le T$ (12)

式中， $\tau$ 表示信号的时延；

由上文可知式(5)的WVD是一条沿 $f=f_0+kt$ 分布的斜直线，利用坐标变换公式(8)得到在 $\left(u\text{,}v\right)$ 平面峰值点位置是：

$u_1=f_0\sin \alpha$ (13)

LFM信号的时延信号在 $\left(t,f\right)$ 平面的WVD为：

$W_{x2}\left(t,f\right)=A^2\delta \left[f-f_0-k\left(t-\tau \right)\right]$ (14)

同理可得其在 $\left(u\text{,}v\right)$ 平面峰值点位置是

$u_2=f_0\sin \alpha +\tau \cos \alpha$ (15)

对比式(13)与式(15)可以看出，取特定角度FRFT的回波信号的峰值点坐标和发射信号峰值点坐标有所不同，回波信号的峰值点坐标和时延值有关 [13] ，联立两式可得时延 $\tau$ ：

$\tau =\frac{u_2-u_1}{\cos \alpha }$ (16)

FRFT在实际工程应用中需要将数据离散并量纲归一化，文献 [14] 说明了量纲归一化后对LFM信号

参数估计的影响，则归一化调频斜率 ${k^{\prime }}_0=-\cot {{\alpha }^{\prime }}_0=\frac{B}{f_s}$ ，最终时延为：

$\tau =\frac{u_2-u_1}{\cos {{\alpha }^{\prime }}_0}\cdot \frac{1}{f_s}$ (17)

2.4. LFM实信号时延估计存在干扰项原因

由于实际中并不存在复信号只有实信号 [15] ，接收到的回波信号为实信号，对其直接做FRFT在 $\left(u\text{,}v\right)$ 平面会出现干扰项从而影响判断峰值点坐标。

LFM信号时域表达式为：

$s\left(t\right)=\exp \left(j2\pi f_{0}t+j\pi k_0{t}^2\right),0\le t\le T$ (17)

对 $s\left(t\right)$ 进行阶数为p的FRFT变换，则可以得到：

$\begin{array}{c}{F}^p\left[s\left(t\right)\right]={\displaystyle {\int }_{-\infty }^{\infty }s}\left(t\right)K_p\left(t,u\right)\text{d}t\\ =A_{\alpha }{\text{e}}^{j\left(\pi u^2\cot \alpha \right)}{\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{j\pi \left(k_0+\cot \alpha \right)t^2}}{\text{e}}^{-2j\pi t\left(u-f_0\sin \alpha \right)}\text{d}t\end{array}$ (18)

当信号的调频率 $k_0$ 的值为 $-\cot \alpha$ 时，式(18)变为：

$F^p\left[s\left(t\right)\right]=A_{\alpha }{\text{e}}^{j\left(\pi u^2\cot \alpha \right)}{\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{-2j\pi t\left(u-f_0\sin \alpha \right)}}\text{d}t=A_{\alpha }{\text{e}}^{j\left(\pi u^2\cot \alpha \right)}\delta \left(u-f_0\sin \alpha \right)/2\pi$ (19)

即当LFM信号在阶数p满足 $k_0=-\cot \alpha =-\cot \left(p\pi /2\right)$ 的分数阶Fourier变换域中呈现冲激响应特性，且能量聚集在 $u=f_0\sin \alpha$ 的位置上。

将欧拉公式 ${\text{e}}^{jx}=\cos x+j\sin x$ 带入式(17)得：

$s\left(t\right)=\cos \left(2\pi f_{0}t+\pi k_0{t}^2\right)+j\sin \left(2\pi f_{0}t+\pi k_0{t}^2\right),0\le t\le T$ (20)

其中 $\cos \left(2\pi f_{0}t+\pi k_0{t}^2\right)$ 为信号实部， $j\sin \left(2\pi f_{0}t+\pi k_0{t}^2\right)$ 为信号虚部。则LFM实信号时域表达式为：

$\begin{array}{c}R\left[s\left(t\right)\right]=s\left(t\right)-j\sin \left(2\pi f_{0}t+\pi k_0{t}^2\right)\\ ={\text{e}}^{j2\pi f_{0}t+j\pi k_0{t}^2}-j\left(\frac{{\text{e}}^{j2\pi f_{0}t+j\pi k_0{t}^2}-{\text{e}}^{-j2\pi f_{0}t-j\pi k_0{t}^2}}{2j}\right)\\ =\frac{{\text{e}}^{j2\pi f_{0}t+j\pi k_0{t}^2}}{2}-\frac{{\text{e}}^{-j2\pi f_{0}t-j\pi k_0{t}^2}}{2}\end{array}$ (21)

同理可得对 $R\left[s\left(t\right)\right]$ 进行阶数p满足 $k_0=-\cot \alpha =-\cot \left(p\pi /2\right)$ 的FRFT可得：

$F^p\left\{R\left[s\left(t\right)\right]\right\}=\frac{A_{\alpha }{\text{e}}^{j\left(\pi u^2\cot \alpha \right)}\delta \left(u-f_0\sin \alpha \right)}{4\pi }-\frac{A_{\alpha }{\text{e}}^{j\left(\pi u^2\cot \alpha \right)}{\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{j\pi \left(-2\cot \alpha \right)t^2}{\text{e}}^{-2j\pi t\left(u-f_0\sin \alpha \right)}\text{d}t}}{2}$ (22)

即LFM实信号特定p阶的FRFT在变换域中为冲激响应和 $\frac{A_{\alpha }{\text{e}}^{j\left(\pi u^2\cot \alpha \right)}{\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{j\pi \left(-2\cot \alpha \right)t^2}{\text{e}}^{-2j\pi t\left(u-f_0\sin \alpha \right)}\text{d}t}}{2}$ 干扰项的叠加，当回波信号峰值位于干扰项附近时，回波信号峰值点将会淹没在干扰项中影响时延估计，如图5所示：

Figure 5. FRFT of LFM real signal

图5. LFM实信号的FRFT

3. 目标检测相关技术研究

3.1. 正交上变频

进行目标检测时，需要将LFM复信号转换为实信号并调制到适合信道传输的频段上发射出去。如果将LFM信号直接与载波混频，进行频谱搬移后发射，混频后既有和频也有差频，造成频谱资源浪费。因此采用正交上变频技术。对LFM信号正交上变频的原理如下图6所示。

其中信号实部数据使用乘法器乘上载频 $\cos \left(2\pi f_{1}t\right)$ ，信号虚部数据则乘上相互正交的载频 $\sin \left(2\pi f_{1}t\right)$ ，相加求和后输出 $S\left(t\right)$ ，即将复信号调制到中频实信号上，供发射端发射出去。

正交上变频后的中频实信号 $S\left(t\right)$ 的表达式为：

Figure 6. Schematic diagram of orthogonal up conversion

图6. 正交上变频原理图

$\begin{array}{c}S\left(t\right)=\cos \left(2\pi f_{0}t+\pi k_0{t}^2\right)\cdot \cos \left(2\pi f_{1}t\right)-\sin \left(2\pi f_{0}t+\pi k_0{t}^2\right)\cdot \sin \left(2\pi f_{1}t\right)\\ =\frac{1}{2}\cdot \left[\cos \left(2\pi f_{0}t+\pi k_0{t}^2+2\pi f_{1}t\right)+\cos \left(2\pi f_{0}t+\pi k_0{t}^2-2\pi f_{1}t\right)\right]\\ +\frac{1}{2}\cdot \left[\cos \left(2\pi f_{0}t+\pi k_0{t}^2+2\pi f_{1}t\right)-\cos \left(2\pi f_{0}t+\pi k_0{t}^2-2\pi f_{1}t\right)\right]\\ =\cos \left[2\pi \left(f_0+f_1\right)t+\pi k_0{t}^2\right]\end{array}$ (23)

3.2. 正交下变频

接收到的信号为实信号，构造解析信号可以去除直接对接收到的实信号做FRFT的干扰项。采用正交下变频技术可以去除接收信号中的中频载波并无损的提取出信号的同相部分(实部)和正交部分(虚部)构造解析信号。正交下变频的原理如下图7所示：

Figure 7. Schematic diagram of orthogonal down conversion

图7. 正交下变频原理图

首先将中频回波信号分别与两路相位差90˚的 $\cos \left(2\pi f_{1}t\right)$ 和 $\sin \left(2\pi f_{1}t\right)$ 进行混频，混频后的输出包含了高频分量，使用低通滤波器LPF可以去除这两项高频分量，得到测试信号实部数据和虚部数据，合成后就将接收的实信号转换为解析信号。

其中实部数据为：

$\begin{array}{c}I\left(t\right)=S\left(t\right)\cdot \cos \left(2\pi f_{1}t\right)\\ =\cos \left[2\pi \left(f_0+f_1\right)t+\pi k_0{t}^2\right]\cdot \cos \left(2\pi f_{1}t\right)\\ =\frac{1}{2}\cdot \left\{\cos \left[2\pi \left(f_0+f_1\right)t+\pi k_0{t}^2+2\pi f_{1}t\right]+\cos \left[2\pi \left(f_0+f_1\right)t+\pi k_0{t}^2-2\pi f_{1}t\right]\right\}\\ =\frac{1}{2}\cdot \left\{\cos \left[2\pi \left(f_0+2f_1\right)t+\pi k_0{t}^2\right]+\cos \left(2\pi f_{0}t+\pi k_0{t}^2\right)\right\}\end{array}$ (24)

其中虚部数据为：

$\begin{array}{c}Q\left(t\right)=S\left(t\right)\cdot \sin \left(2\pi f_{1}t\right)\\ =\frac{1}{2}\cdot \left\{\sin \left[2\pi \left(f_0+2f_1\right)t+\pi k_0{t}^2\right]\text{+}\sin \left(2\pi f_{0}t+\pi k_0{t}^2\right)\right\}\end{array}$ (25)

3.3. 基于FRFT的LFM信号时延估计具体步骤

根据上文给出基于FRFT的LFM信号时延估计具体步骤：

将固定带宽和时宽的LFM信号做正交上变频调制到中频实信号后经发射端发射出去。

接收端将接收到的实信号做正交下变频转换为解析信号。

将解析信号量纲归一化后，根据LFM信号带宽和时宽得出调频率 $k^{\prime }$ ，进而得出匹配阶次 $p^{\prime }$ ，然后对接收信号做 $p^{\prime }$ 阶FRFT，在分数域中寻找发射信号峰值点u₁和回波信号u₂峰值点。

将u₁和u₂带入式(17)得出时延 $\tau$ ，计算出目标距离。

4. MATLAB仿真

4.1. 正交上变频仿真

本文的LFM信号参数设置为：幅值 $A=1\text{V}$ ，起始频率 $f_0=0$ ，时宽 $T=10\mu \text{s}$ ，带宽 $B=10\text{MHz}$ 采样频率 $f_s=200\text{MHz}$ ，采样点数 $n=2000$ ，使用MATLAB对上述信号进行仿真，得到如图8所示LFM信号时域和频域波形：

Figure 8. Real and imaginary time-domain and frequency-domain waveforms of LFM signals

图8. LFM信号实部、虚部时域和频域波形

取载频频率 $f_{\text{1}}=\text{30}\text{MHz}$ ，按上述原理进行正交上变频，变换后信号时域和频域波形如图9所示。

对比图8与图9可得，经正交上变频后，LFM信号有用的频率成分从0~10 MHz调制到了载波频率 $f_{\text{1}}$ 上，其中只包含合频，不包含差频，消除了多余的频谱分量，且产生了对称的负频率量，模拟了发射信号从复信号转换为中频实信号供发射机发射。

Figure 9. The time-domain and frequency-domain waveforms of the signal after orthogonal upconversion

图9. 正交上变频后信号时域和频域波形

4.2. 正交下变频仿真

将发射信号添加信噪比 $\text{SNR}=10\text{dB}$ 的噪声并衰减为0.2 V模拟目标点2.3 km处的反射信号，发射信号与反射信号叠加模拟接收到的信号，则接收信号时域和频域波形如图10所示：

Figure 10. Received signal time-domain and frequency-domain waveforms

图10. 接收信号时域和频域波形

将接收信号正交下变频混频后低通滤波，在MATLAB中设置FIR低通滤波器阶数 $N=50$ ，截止频率为LFM信号带宽 $B=10\text{MHz}$ ，滤波去除混频产生的 $\left(f_0+2f_1\right)$ 频率成分后接收信号实部I和虚部Q时域和频域波形如图11、图12所示：

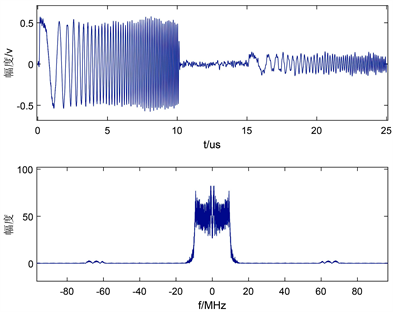
Figure 11. Real part data after low-pass filtering

图11. 低通滤波后实部数据

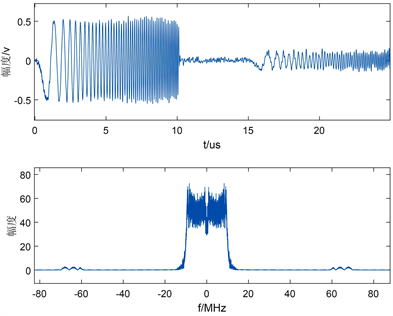
Figure 12. Imaginary part data after low-pass filtering

图12. 低通滤波后虚部数据

对比图10和图11、图12可以看出，接收信号经正交下变频后去除了中频载波的频率成分，并提取出了接收信号的实部和虚部。令 $S\left(t\right)=I\left(t\right)+j\cdot Q\left(t\right)$ ，进一步组合成为复数解析信号，合成信号波形如图13所示。

4.3. 时延估计仿真

将正交下变频合成的信号经FRFT算法提取有用信息进行时延估计，算法处理结果如图14所示。

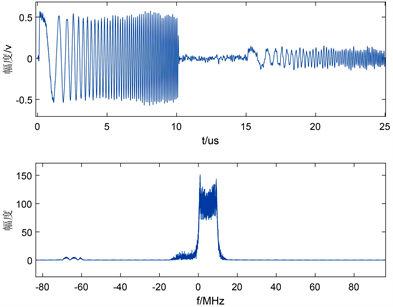
Figure 13. Orthogonal down conversion synthesis signal

图13. 正交下变频合成信号

Figure 14. Imaginary part data after low-pass filtering

图14. FRFT变换图

距离为0和距离为2.3km信号FRFT峰值位置点数分别为951和1105处，带入式(17)得

$\tau =\frac{u_2-u_1}{\cos {{\alpha }^{\prime }}_{\text{0}}}\cdot \frac{1}{f_s}=\frac{1105-951}{\cos \left[\mathrm{arccot}\frac{10\times {10}^6}{200\times {10}^6}\right]}\cdot \frac{1}{200\times {10}^6}=\text{15}\text{.419}\times {10}^{-6}\text{s}$

则目标距离 $R=\frac{c}{2}\times \tau =22963\text{m}$ 。

按照上述步骤模拟1 km、3 km和5 km距离处目标点的反射信号，进行基于FRFT的LFM信号时延估计，仿真结果如表1。

Table 1. Simulate test results

表1. 仿真检测结果

从表1可知，通过仿真模拟目标距离检测的误差率在3%以内，该仿真结果表明基于FRFT的LFM信号时延估计方法能有效地检测出低信噪比目标距离。

5. 结论

本文基于FRFT算法，结合FRFT算法在特定分数域内对LFM信号能量聚集特性，对LFM信号进行时延估计研究，得出LFM时延与分数域峰值差有关，根据数据离散量纲归一化后的影响给出了时延估计计算公式。同时针对实际应用中对接收到实信号直接进行时延估计会产生干扰项的问题，通过正交下变频构造解析信号提高了时延估计准确性。通过检测不同目标距离进行仿真实验，验证了FRFT时延估计的科学性和有效性。实验结果表明该方法能准确地实现时延估计，适用于工程实践。